当前位置:网站首页>98. 验证二叉搜索树 ●●
98. 验证二叉搜索树 ●●
2022-07-05 23:06:00 【chenyfan_】
98. 验证二叉搜索树 ●●
描述
给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。
有效 二叉搜索树定义如下:
- 节点的左子树只包含 小于 当前节点的数。
- 节点的右子树只包含 大于 当前节点的数。
- 所有左子树和右子树自身必须也是二叉搜索树。
示例
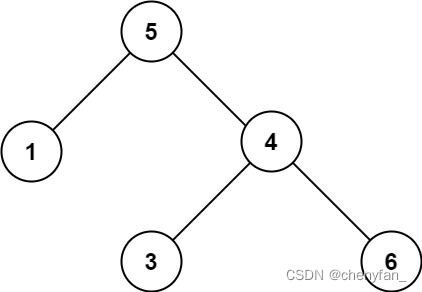
输入:root = [5,1,4,null,null,3,6]
输出:false
解释:根节点的值是 5 ,但是右子节点的值是 4 。
题解
性质:中序遍历下,输出的二叉搜索树节点的数值是有序序列。
因此可以中序遍历用数组记录所有元素,再遍历数组进行判断。
但也可以全局定义一个待比较值,直接在中序遍历过程中进行比较判断并不断更新待比较值,需要注意的是:
不能单纯的比较左节点小于中间节点,右节点大于中间节点就完事了,我们要比较的是 左子树所有节点小于中间节点,右子树所有节点大于中间节点,因此还要与前面的节点进行比较。
1. 中序遍历 递归
- 初始化待比较值为long long型最小值,应对题目中存在整型最小值的情况;
class Solution {
public:
long long preValue = LONG_MIN; // 初始化前一个数为长型最小值
bool isValidBST(TreeNode* root) {
if(!root) return true;
bool left = isValidBST(root->left); // 左
if(root->val <= preValue){
// 中
return false; // 中序遍历时与前一个数比较判断有序性
}else{
preValue = root->val;
}
bool right = isValidBST(root->right); // 右
return left && right; // 左右子树的有效性
}
};
- 或者定义待比较值为节点类型
class Solution {
public:
TreeNode* preNode = nullptr; // 待比较节点
bool isValidBST(TreeNode* root) {
if(!root) return true;
bool left = isValidBST(root->left); // 左
if(preNode != nullptr && root->val <= preNode->val){
// 中
return false; // 无效,退出
}else{
preNode = root; // 中序遍历时与前一个数比较判断有序性
}
bool right = isValidBST(root->right); // 右
return left && right; // 左右子树的有效性
}
};
2. 中序遍历 迭代
class Solution {
public:
bool isValidBST(TreeNode* root) {
stack<TreeNode*> st;
TreeNode* preNode = nullptr; // 待比较节点
TreeNode* curr = root;
while(curr != nullptr || !st.empty()){
if(curr){
st.push(curr); // 节点入栈
curr = curr->left; // 节点指针指向左孩子
}else{
// 遍历完所有左孩子
curr = st.top();
st.pop(); // 中
if(preNode && curr->val <= preNode->val) return false;
preNode = curr;
curr = curr->right; // 节点指针指向右孩子
}
}
return true;
}
};
- 利用空指针标记的统一迭代写法
class Solution {
public:
bool isValidBST(TreeNode* root) {
stack<TreeNode*> st;
TreeNode* curr = nullptr;
TreeNode* preNode = nullptr; // 前一个元素,待比较节点
st.push(root);
while(!st.empty()){
curr = st.top();
st.pop(); // 对非空栈顶的孩子进行访问
if(curr != nullptr){
// 入栈顺序为:右-中-null-左; 出栈顺序为:左-null-中-右
if(curr->right) st.push(curr->right);
st.push(curr);
st.push(nullptr);
if(curr->left) st.push(curr->left);
}else{
curr = st.top(); // null后面的元素表示已经访问过,此时需要弹出并取出元素值
st.pop();
if(preNode != nullptr && curr->val <= preNode->val) return false;
preNode = curr;
}
}
return true;
}
};
边栏推荐
猜你喜欢
TypeError: this. getOptions is not a function
Data type, variable declaration, global variable and i/o mapping of PLC programming basis (CoDeSys)

Alibaba Tianchi SQL training camp task4 learning notes
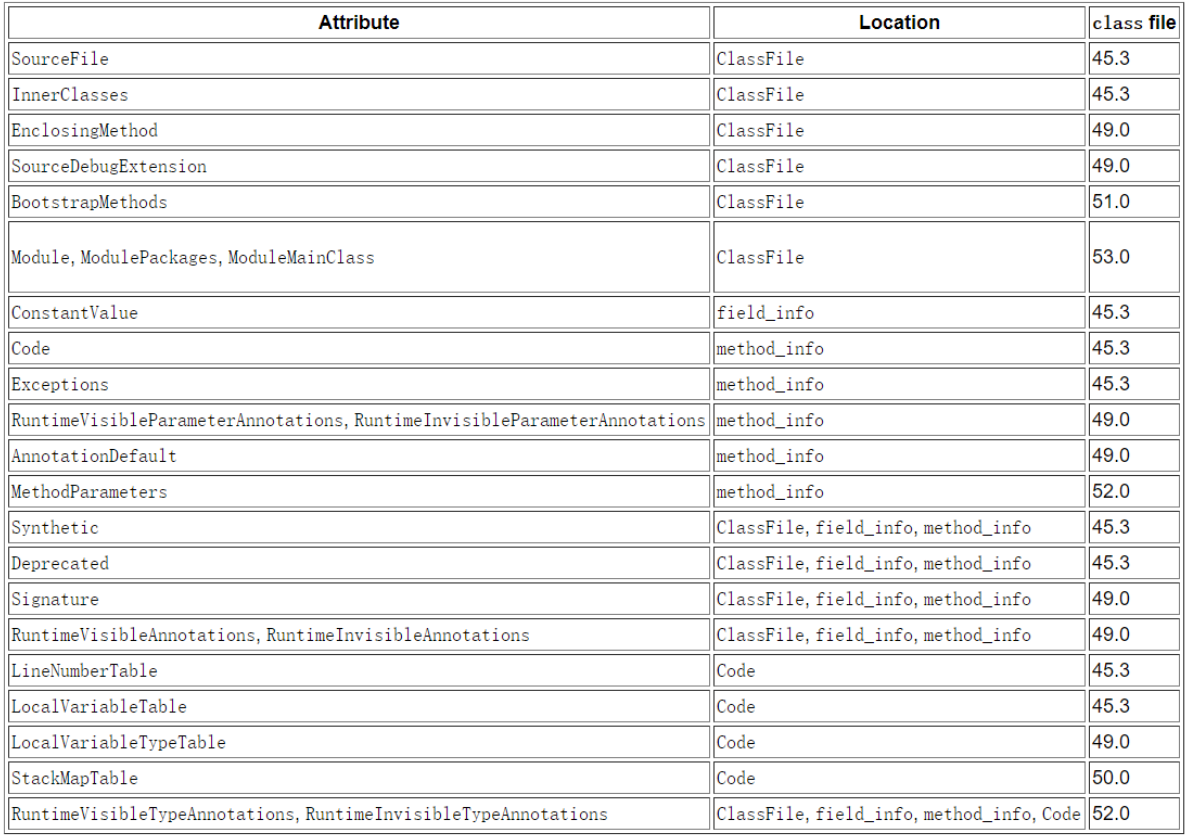
One article deals with the microstructure and instructions of class

Sum of two numbers, sum of three numbers (sort + double pointer)
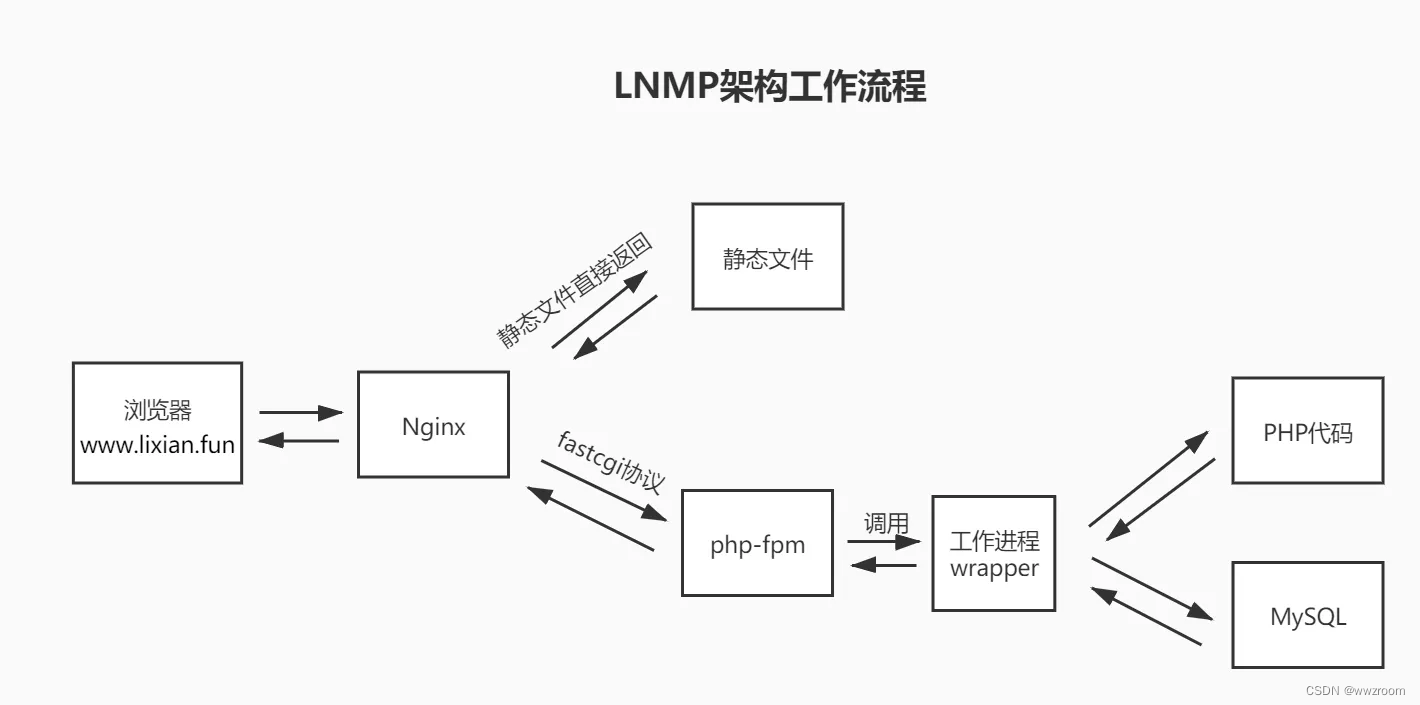
Week 17 homework

14种神笔记方法,只需选择1招,让你的学习和工作效率提高100倍!
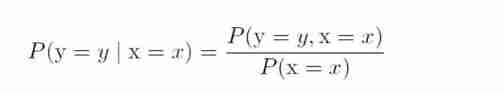
Marginal probability and conditional probability
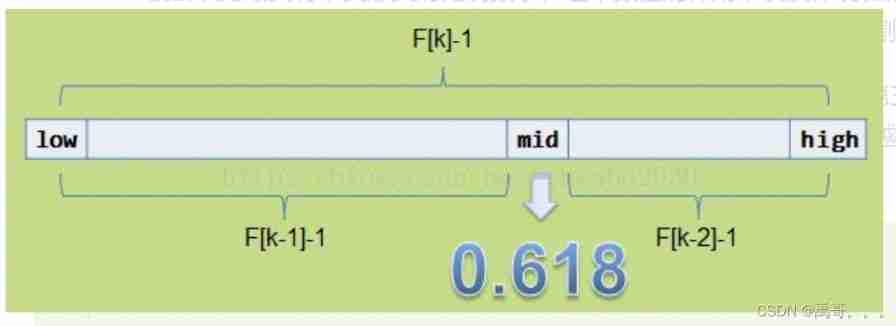
fibonacci search
基于脉冲神经网络的物体检测
随机推荐
秒杀系统的设计与实现思路
Déterminer si un arbre binaire est un arbre binaire complet
VS2010 writes DLL and unit test of dynamic link library, and transfers the correctness of DLL test
Creative mode 1 - single case mode
一文搞定JVM的内存结构
判斷二叉樹是否為完全二叉樹
LabVIEW打开PNG 图像正常而 Photoshop打开得到全黑的图像
openresty ngx_lua正则表达式
Use of grpc interceptor
【Note17】PECI(Platform Environment Control Interface)
2022 G3 boiler water treatment simulation examination and G3 boiler water treatment simulation examination question bank
Simple and beautiful method of PPT color matching
3:第一章:认识JVM规范2:JVM规范,简介;
(4)UART應用設計及仿真驗證2 —— TX模塊設計(無狀態機)
Basic knowledge of database (interview)
It is proved that POJ 1014 module is optimized and pruned, and some recursion is wrong
The maximum happiness of the party
Code farmers to improve productivity
How to quickly understand complex businesses and systematically think about problems?
数学公式截图识别神器Mathpix无限使用教程