当前位置:网站首页>并查集实践
并查集实践
2022-07-05 22:50:00 【BugMaker-shen】
是不是亲戚问题

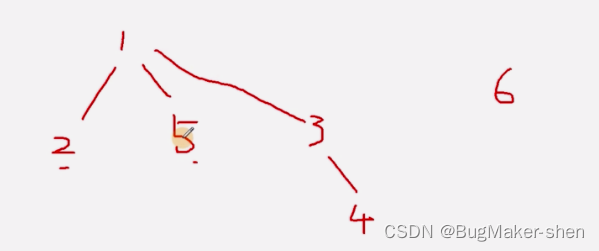
我们使用merge的优化,就不使用find的优化了
#include <iostream>
#include <vector>
using namespace std;
int SIZE = 0;
int* parent = nullptr; // 记录每个节点的父节点
int* height = nullptr; // 记录根节点的层高
// 返回x所在树的根节点的编号
int find_root(int x) {
if (x <= 0 || x >= SIZE) {
return -1;
}
while (x != parent[x]) {
x = parent[x];
}
return x;
}
// 合并x和y所在的集合
void merge(int x, int y) {
x = find_root(x);
y = find_root(y);
if (x != y) {
// 这里x和y都是根节点,谁矮谁作为孩子节点
if (height[x] > height[y]) {
parent[y] = x;
}
else {
if (height[x] == height[y]) {
// y作为合并以后树的根,根节点高度要+1
height[y]++;
}
parent[x] = y;
}
}
}
int main() {
int m = 0;
int p = 0;
int n = 0;
cin >> n >> m >> p;
SIZE = n + 1;
parent = new int[SIZE];
height = new int[SIZE];
for (int i = 0; i < SIZE; i++) {
height[i] = 1;
parent[i] = i; // 一开始,每个节点的父节点就是自己
}
int p1, p2; // 两个人
for (int i = 0; i < m; i++) {
cin >> p1 >> p2;
merge(p1, p2);
}
vector<pair<int, int>> query;
for (int i = 0; i < p; i++) {
cin >> p1 >> p2;
query.push_back(pair<int, int>(p1, p2));
}
for (auto q : query) {
cout << (find_root(q.first) == find_root(q.second) ? "YES" : "NO") << endl;
}
delete[] parent;
delete[] height;
parent = nullptr;
height = nullptr;
return 0;
}
/* 6 5 3 1 2 1 5 3 4 5 2 1 3 1 4 2 3 5 6 */
躲避拥堵的最佳路线
3 3 1 3 # 3个区、3条边、从1区到3区
1 2 2 # 从1区到2区的拥挤度为2
2 3 1
1 3 3
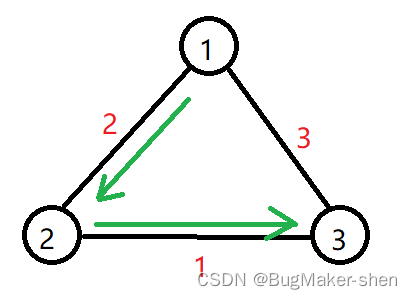
题目说规划一条路径,使得经过道路的拥挤度的最大值最小。该测试用例输出2,是说我们从1区到3区,可以走1->2->3,此时拥挤度的最大值为2;也可以走1->3,此时拥挤度的最大值为3;故该测试用例输出2
我们使用kruskal算法,先从拥挤度小的边开始选取,直到连通s区和t区,这样最后一条选取的边一定是已选道路拥挤度最大的,未选道路拥挤度最小的,这样就能做到在连通的基础上所选取的最大值最小
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int* parent = nullptr;
struct Edge {
Edge(int start, int end, int w)
: start_(start)
, end_(end)
, w_(w)
{
}
int start_;
int end_;
int w_;
};
// 找编号为x的节点的根节点
int find(int x) {
if (x == parent[x]) {
return x;
}
else {
// find优化,查找根节点的过程中,把遍历过的节点的父节点都改成根节点
parent[x] = find(parent[x]);
return parent[x];
}
}
int main(){
int n, num_edge, s, t;
cin >> n >> num_edge >> s >> t;
parent = new int[n + 1](); // n个区,为了让编号和下标对应,多开辟一个
vector<Edge> edges;
int start, end, w;
for (int i = 0; i < num_edge; i++) {
cin >> start >> end >> w;
edges.emplace_back(start, end, w);
// 初始化parent数组
parent[start] = start;
parent[end] = end;
}
// 边进行升序排列
sort(edges.begin(), edges.end(),
[](const Edge& e1, const Edge& e2) ->bool{
return e1.w_ < e2.w_;
});
for (int i = 0; i < num_edge; i++) {
int root1 = find(edges[i].start_);
int root2 = find(edges[i].end_);
if (root1 != root2) {
// 根节点不同,可以连接
parent[root1] = root2;
if (find(s) == find(t)) {
// 选择了新的边,才会判断是否连通了s区和t区;本轮循环没有选择新的边,则没有必要判断是否连通s区和t区
cout << edges[i].w_ << endl;
}
}
}
delete[] parent;
return 0;
}
/* 3 3 1 3 1 2 2 2 3 1 1 3 3 */
边栏推荐
- Nacos installation and service registration
- Douban scoring applet Part-2
- 谷歌地图案例
- 2022 R2 mobile pressure vessel filling review simulation examination and R2 mobile pressure vessel filling examination questions
- Using LNMP to build WordPress sites
- Un article traite de la microstructure et des instructions de la classe
- VOT toolkit environment configuration and use
- Common JVM tools and optimization strategies
- Realize reverse proxy client IP transparent transmission
- Function default parameters, function placeholder parameters, function overloading and precautions
猜你喜欢
![[digital signal denoising] improved wavelet modulus maxima digital signal denoising based on MATLAB [including Matlab source code 1710]](/img/b4/af689abb3ad4e25988f2d17152406e.jpg)
[digital signal denoising] improved wavelet modulus maxima digital signal denoising based on MATLAB [including Matlab source code 1710]

Hcip day 11 (BGP agreement)
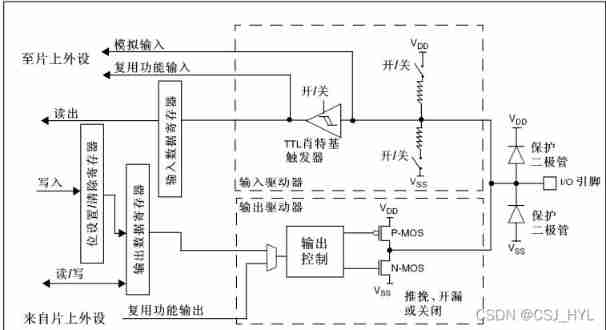
Getting started stm32--gpio (running lantern) (nanny level)

Google Maps case
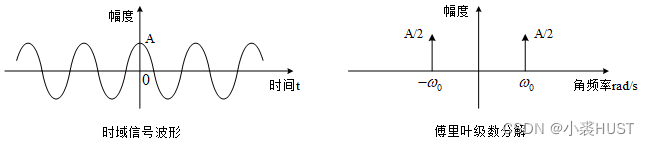
Overview of Fourier analysis
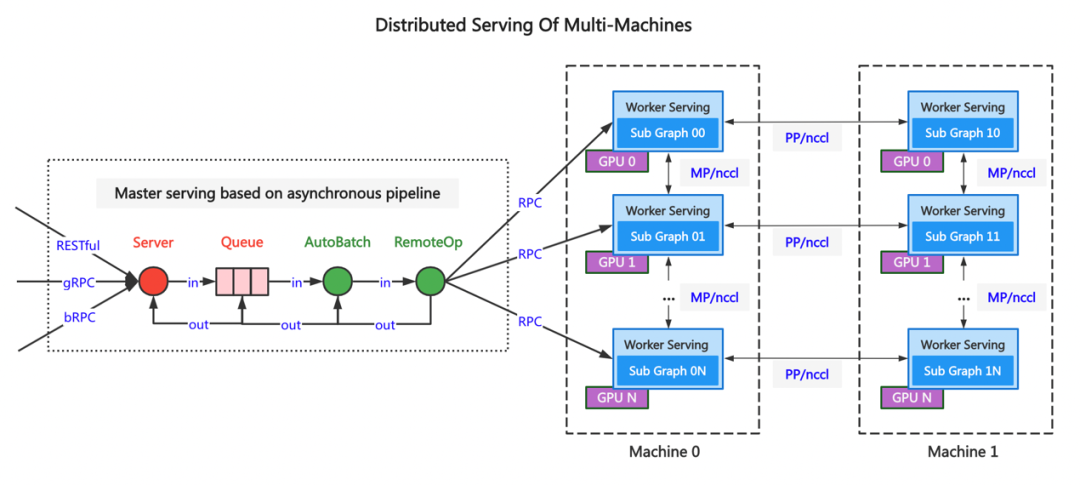
Paddle Serving v0.9.0 重磅发布多机多卡分布式推理框架
Editor extensions in unity
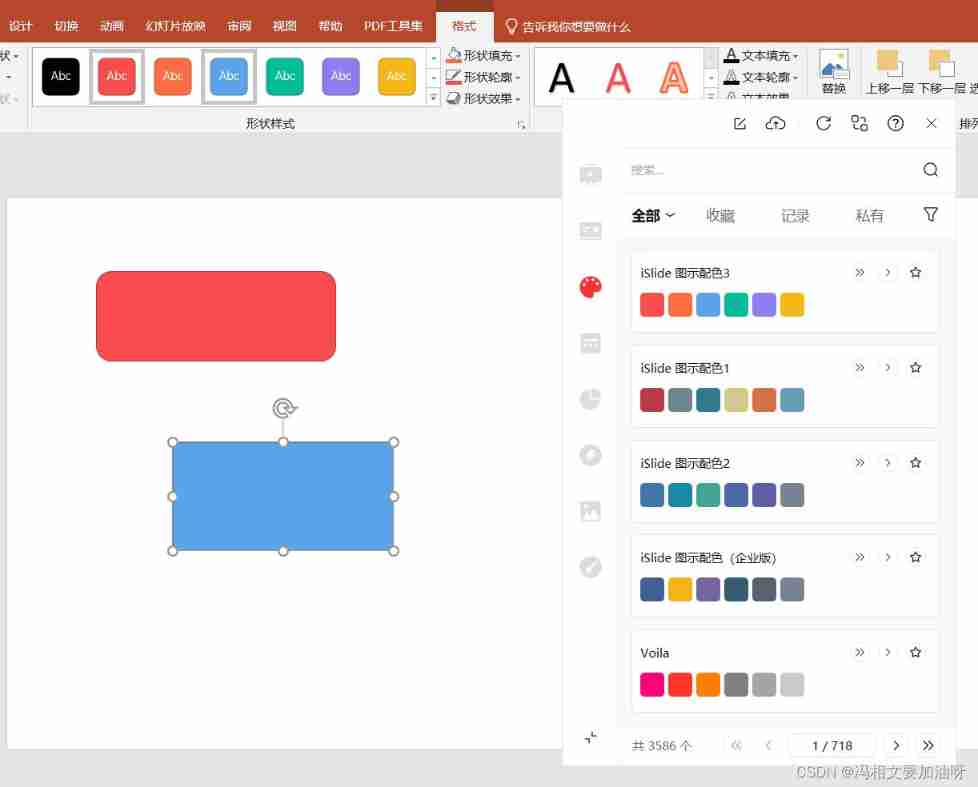
Simple and beautiful method of PPT color matching
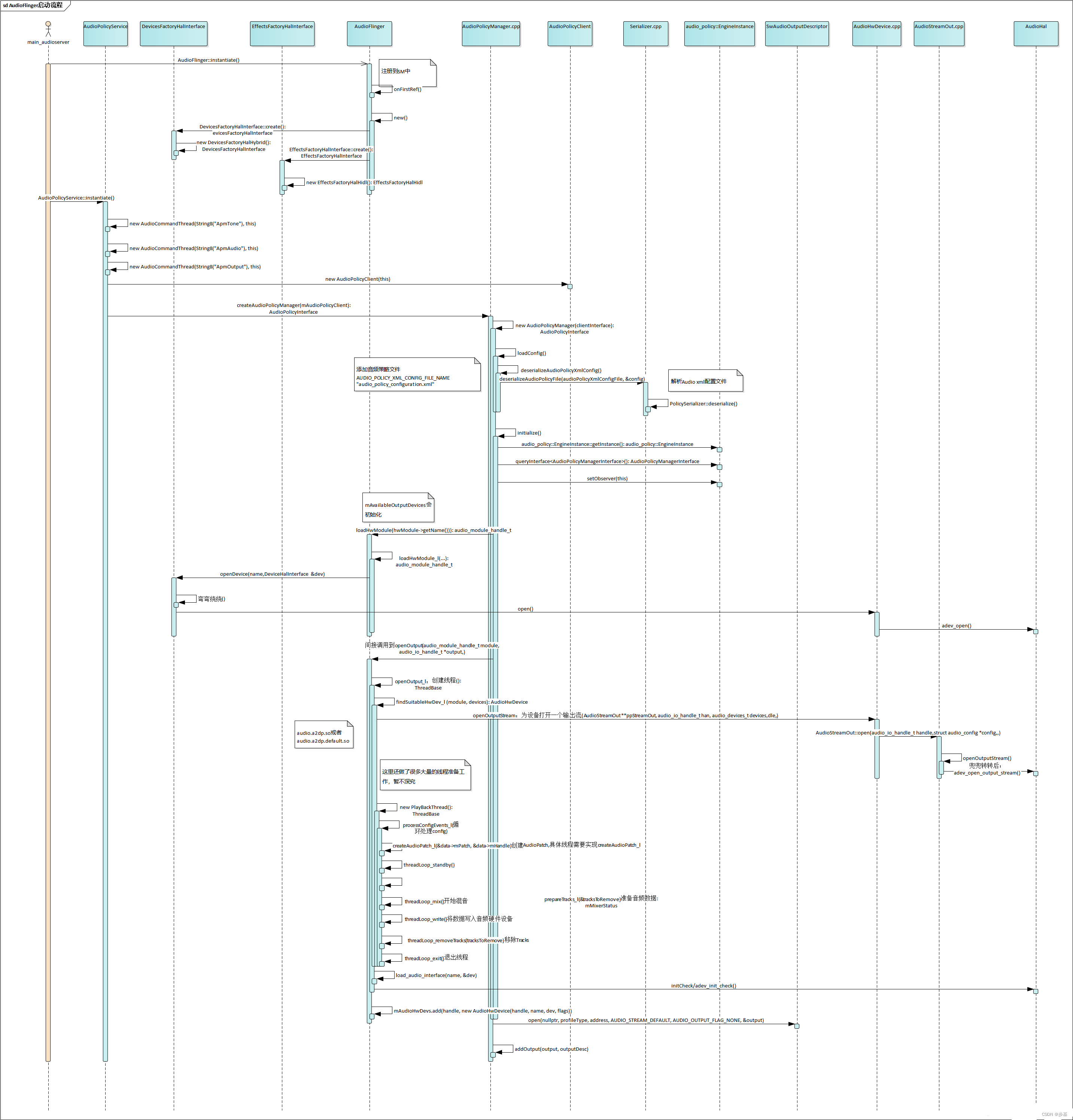
audiopolicy

LeetCode102. Sequence traversal of binary tree (output by layer and unified output)
随机推荐
Using LNMP to build WordPress sites
如何快速理解复杂业务,系统思考问题?
Thinkphp5.1 cross domain problem solving
Finally understand what dynamic planning is
VOT Toolkit环境配置与使用
VOT toolkit environment configuration and use
2022.02.13 - SX10-30. Home raiding II
Evolution of APK reinforcement technology, APK reinforcement technology and shortcomings
我对新中台模型的一些经验思考总结
一文搞定class的微观结构和指令
SPSS analysis of employment problems of college graduates
Solve the problem of "no input file specified" when ThinkPHP starts
Marginal probability and conditional probability
openresty ngx_ Lua regular expression
Overview of Fourier analysis
Metasploit(msf)利用ms17_010(永恒之蓝)出现Encoding::UndefinedConversionError问题
Douban scoring applet Part-2
Masked Autoencoders Are Scalable Vision Learners (MAE)
Vision Transformer (ViT)
Element positioning of Web Automation