Let's start with the outline of this article , This is for me mindmap A brain map , After that, I will continue to improve , Gradually improve other topics .
You can also use vscode blink-mind Open the source file to view , There are some notes that you can click to view . The source file can go to my official account 《 Force buckle plus 》 Get back to the brain map , In the future, the brain map will continue to update more content .vscode Plug-in address : https://marketplace.visualstu...
Hello everyone , I am a lucifer. Today's topic for you is 《 Linked list 》. Many people find linked lists a difficult topic . actually , As long as you have the knack , It's not that hard . Next , Let's talk about .
List tags stay leetcode Altogether 54 Problem . To prepare for this project , It took me a few days to get leetcode Almost all the linked list titles have been swiped .

It can be seen that , Except for six locked , I've done everything else . But in fact , There's no difficulty with these six locks , Even with other things 48 The problem is almost .
By focusing on these questions , I found some interesting information , Let's share it with you today .
<!-- more -->
brief introduction
Various data structures , Whether it's a queue , A linear data structure such as a stack is still a tree , The nonlinear data structure of graphs , Basically, the bottom layer is arrays and lists . Whether you're using arrays or linked lists , It's all computer memory , Physical memory is made up of memory units of the same size , Pictured :

( chart 1. Physical memory )
While arrays and linked lists use physical memory , Both are very different in the use of physics , Pictured :

( chart 2. Physical storage of arrays and linked lists )
It's not hard to see. , Arrays and linked lists are just two ways to use physical memory .
Arrays are contiguous memory spaces , Usually the size of each unit is fixed , So you can randomly access . The linked list is not necessarily continuous , So it can only be found in other ways , Usually we do it through a name called next Pointer to traverse to find . A linked list is actually a structure . For example, a possible definition of a single linked list can be :
interface ListNode<T> {
data: T;
next: ListNode;
}data It's the data domain , Storing data ,next Is a pointer to the next node .
A linked list is a physical storage unit that is discontinuous 、 Nonsequential storage structure , The logical order of data elements is achieved by the order of Pointers in a linked list . A linked list consists of a series of nodes ( Each element in a linked list is called a node ) form , Nodes can be generated dynamically at run time .
From the physical structure diagram above, we can see that the array is a continuous space , Each item of the array is closely linked , So if you want to insert and delete operations, it's very troublesome . The time complexity of inserting and deleting array headers is $O(N)$, And the average complexity is $O(N)$, Only insertion and deletion of the tail is $O(1)$. Simply speaking ” Arrays are particularly friendly to queries , Unfriendly to delete and add “. To solve this problem , There is a linked list data structure . Linked list is suitable for data that needs to have a certain order , But it needs to be added and deleted frequently , Please refer to the following for details 《 Basic operations of linked lists 》 Section .

( chart 3. A typical logical representation of linked list )
All of the following diagrams are based on logical structure , Not the physical structure
The linked list has only one back drive node next, If it is a bidirectional linked list, there will also be a precursor node pre.
Have you ever thought about why there are only binary trees , And there's no fork tree . In fact, linked lists are special trees , It's a fork tree .
Basic operations of linked lists
To write the title of a linked list , It is necessary to be familiar with the basic operations and complexity of linked lists .
Insert
Insertion only needs to consider the location of the insertion, the precursor node and the successor node ( In the case of bidirectional linked list, the successor nodes need to be updated ) that will do , Other nodes are not affected , Therefore, given the pointer, the operation time complexity of insertion is O(1). Here, the pointer in the given pointer refers to the precursor node of the insertion position .
Pseudo code :
temp = The precursor node of the position to be inserted .next
The precursor node of the position to be inserted .next = To insert the pointer
To insert the pointer .next = temp
If there is no given pointer , We need to traverse to find the node first , So the worst case time complexity is O(N).
Tips 1: Consider the head and tail pointer .Tips 2: Beginners recommend drawing first , Write code again . When you're proficient , Naturally, there's no need to draw .
Delete
Only need to delete the node's precursor pointer next Correct the pointer to its next node , Pay attention to The boundary conditions .
Pseudo code :
The precursor node of the location to be deleted .next = The precursor node of the location to be deleted .next.nextTips 1: Consider the head and tail pointer .Tips 2: Beginners recommend drawing first , Write code again . When you're proficient , Naturally, there's no need to draw .
Traverse
Traversal is relatively simple , Directly on pseudo code .
Iterate pseudo code :
Pointer to the current = The head pointer
while The current node is not empty {
print( Current node )
Pointer to the current = Pointer to the current .next
}
A recursive pseudo code of preorder traversal :
dfs(cur) {
if The current node is empty return
print(cur.val)
return dfs(cur.next)
}How much difference is there between a linked list and an array ?
Friends who are familiar with me should often hear me say a word , That's it Arrays and linked lists are also used as linear array structures , Both are the same in many conveniences , There are only differences in the subtle operation and usage scenarios . And use scenarios , It is difficult to examine directly in the subject .
actually , Use scenarios can be memorized by rote .
therefore , For us to do the problem , The difference between the two is usually just a subtle operational difference . So people may not feel strong enough , Let me give you a few examples .
Traversal of array :
for(int i = 0; i < arr.size();i++) {
print(arr[i])
}
Traversal of the list :
for (ListNode cur = head; cur != null; cur = cur.next) {
print(cur.val)
}Is it very similar ?
It can be seen that the logic of the two is consistent , It's just a little bit different . such as :
- Array is index ++
- The list is the cur = cur.next
What if we need to traverse in reverse order ?
for(int i = arr.size() - 1; i > - 1;i--) {
print(arr[i])
}If it's a linked list , It is usually necessary to use a double linked list . And the two-way linked list in the force of the problem is very few , So most of you can't get the precursor node , This is also why many times they record a precursor node by themselves pre Why .
for (ListNode cur = tail; cur != null; cur = cur.pre) {
print(cur.val)
}If you add an element to the end of an array, it is :
arr.push(1)Chain words , Many languages don't have built-in array types . For example, force buckles usually use the following classes to simulate .
public class ListNode {
int val;
ListNode next;
ListNode() {}
ListNode(int val) { this.val = val; }
ListNode(int val, ListNode next) { this.val = val; this.next = next; }
}We can't call push Methodical . Think about it , If you do this , How do you do ? You can think about it for yourself first , Look down again .
3...2...1
ok, It's very simple .
// hypothesis cur It's the tail node of a linked list
tail.next = new ListNode('lucifer')
tail = tail.nextAfter two lines of code above , tail Still pointing to the tail node . Is it simple , Have you learned ?
What's the point ? For example, some topics require you to copy a new linked list , Do you need to create a new chain header , And then they're stitching together (push) Replicated nodes ? This uses .
It's similar to the bottom of the array , A possible array push Underlying implementation :
arr.length += 1
arr[arr.length - 1] = 'lucifer'To sum up , There are many logical similarities between array and linked list , The difference is just some usage scenarios and operation details , For the problem , We usually focus more on the details of the operation . About details , Next, let's introduce , This section mainly let you know the two in the ideological and logical God is similar .
Some of the partners do the list problem, first change the list into an array , And then do it with arrays , I don't recommend it , This is tantamount to denying the value of linked lists , Children should not imitate .
How difficult is the list problem ?
The linked list is really not difficult . There is evidence that linked lists are not difficult . take LeetCode Platform , There are only two difficult topics .

among The first 23 There is basically no linked list operation , A regular “ Merge sort ” That's it , And merging two ordered lists is a simple problem . If you know how to merge and sort arrays and merge two ordered lists , It should be easy to take this question .
Merging two ordered arrays is also a simple topic , The difficulty of the two is almost the same .
And for the first 25 topic , I believe you have read this section , It can also be done .
however , That said , But there are still many children who tell me ” When the pointer goes around, it gets dizzy “, ” It's always a dead circle “ ...... Is the linked list title really so difficult ? How can we crack ? lucifer I have prepared a pithy formula for you One principle , Two types of questions , Three notes , Four techniques , It makes it easy for you to solve the list problem , No longer afraid to tear the list by hand . Let's take a look at the contents of this pithy formula in turn .
One principle
One principle is drawing , Especially for beginners . Whether it is a simple problem or a difficult problem, we must draw a picture , This is a rule throughout the list title .
Drawing can reduce our cognitive burden , It's actually about making drafts , The rationale of the memo is the same , Put the things in your mind on paper . An inappropriate example is that your brain is CPU, The memory of the brain is a register . The capacity of registers is limited , We need to put things that are less frequently used in memory , Use registers where they really need to be , This memory is paper or tablet and everything you can draw .
It doesn't matter whether the painting is good or not , Just be able to see clearly . Sketch with a pen , It's enough to see the relationship .
Two test sites
I've made a list of the links . Find an interesting phenomenon , That is, the test points of the linked list are very single . Except for design questions , There are no two points in the exam :
- Pointer modification
- Splicing of chain list
Pointer modification
Among them, the most typical pointer modification is the list inversion . In fact, the list inversion is not to modify the pointer ?
For arrays, which support random access data structures , It's easy to reverse , Just keep swapping the head and tail .
function reverseArray(arr) {
let left = 0;
let right = arr.length - 1;
while (left < right) {
const temp = arr[left];
arr[left++] = arr[right];
arr[right--] = temp;
}
return arr;
}And for a linked list , It's not that easy . I don't need too many questions about the reverse list .
Today, I wrote a complete list inversion for you , In the future, you can use it directly . Of course , The premise is that we should understand first and then apply .
Next , I want to achieve a reversal Any link list
reverse(self, head: ListNode, tail: ListNode).among head Refers to the head node that needs to be reversed ,tail It's the tail node that needs to be reversed . It's not hard to see. , If head It's the head of the whole list ,tail It's the end of the whole list , That's reversing the entire list , Otherwise, it will reverse the local linked list . Next , We're going to do it .
First , All we have to do is draw . I am here. One principle Part of it talked about .
Here's the picture , It's a partial list that we need to reverse :

And we expect to look like this after the reversal :

It's not hard to see. , Eventually return tail that will do .
Because of the recursion of linked lists , actually , We just reverse the two adjacent , The rest is done in the same way .
A linked list is a recursive data structure , Therefore, the use of recursive thinking to consider the past half the effort , Think about recursion later 《 Three notes 》 Partial expansion .

For two nodes , We just need to change the pointer once , It doesn't seem difficult .
cur.next = pre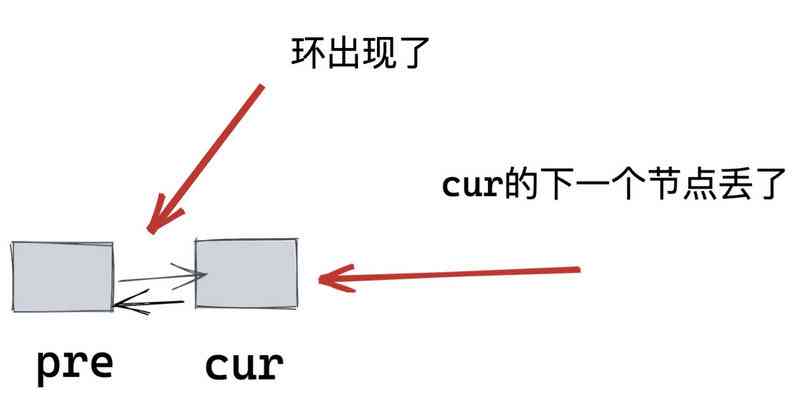
This is the operation , It's not just a ring , Let's keep you in a loop . And let them go their separate ways, which should not be broken .
It's not hard to solve the problem of parting , We just need to reverse before , Just record the next node :
next = cur.next
cur.next = pre
cur = next
And the ring ? actually , There is no need to solve the ring . Because how we go back and forth , So actually , The previous list has been reversed , So my picture above is wrong . The correct picture should be :

So far, , We can write the following code :
# Flip a sublink list , And back to the new head and tail
def reverse(self, head: ListNode, tail: ListNode):
cur = head
pre = None
while cur != tail:
# Leave your contact information
next = cur.next
# Modify pointer
cur.next = pre
# Keep going down
pre = cur
cur = next
# After the reversal of the new head and tail node back out
return tail, headIf you look closely , Will find , our tail It's not actually reversed . The solution is simple , take tail The nodes behind are passed in as parameters .
class Solution:
# Flip a sublink list , And return to the new head and tail
def reverse(self, head: ListNode, tail: ListNode, terminal:ListNode):
cur = head
pre = None
while cur != terminal:
# Leave your contact information
next = cur.next
# Modify pointer
cur.next = pre
# Keep going down
pre = cur
cur = next
# After the reversal of the new head and tail node back out
return tail, headI believe you have a certain understanding of reverse linked list . We will explain this problem in more detail later , Let's make an impression first .
Splicing of chain list
Have you noticed that the chain list always likes to wear it back and forth ( Splicing ) Of ? For example, reverse the linked list II, Another example is the merging of ordered linked lists .
Why do linked lists like to wear them all the time ? actually , This is the value of linked lists , That's what it was designed for !
The value of a linked list lies in its There is no need to require continuity of physical memory , As well as being friendly to inserts and deletions . This can be seen in the physical structure diagram of linked list and array at the beginning of the article .
Therefore, there are many splicing operations in the linked list . If I talked about the basic operation of linked list, you will , I'm sure it won't hurt you . Except for the rings , The border etc. ... ^\_^. Let's look at these questions later .
Three notes
The most error prone part of linked list is what we should pay attention to . The most common mistake in linked lists 90 % Focus on the following three situations :
- There's a ring , Create a dead cycle .
- I can't tell the boundary , Cause boundary conditions to go wrong .
- I don't know how recursion works
Next , Let's look at them one by one .
Ring
There are two test sites in the ring :
- The topic may be related to , Let you judge if there is a ring , And the location of the rings .
- There is no link in the title list , But it's out of the loop by you .
Here we will only discuss the second kind of , And the first one can be used as we mentioned later Fast and slow pointer algorithm .
The simplest and most effective way to avoid loops is to draw pictures , If two or more linked list nodes form a ring , It's easy to see from the diagram . So a simple The practical skill is to draw pictures first , Then all operations on the pointer are reflected in the diagram .
But the list is so long , I can't draw them all . In fact, there is no need to , As mentioned above, linked list is a recursive data structure , Many chain list problems are inherently recursive , For example, reverse the linked list , therefore Just draw a substructure . This knowledge , The one we put in the back Before and after Part of the explanation .
The border
A lot of people are wrong that they don't think about boundaries . A technique for thinking about boundaries is to look at the topic information .
- If the header node of the topic may be removed , So consider using virtual nodes , such The head node becomes the middle node , You don't need to make a special judgment for the head node .
- The title doesn't return you to the original head node , It's the tail node or some other intermediate node , Pay attention to the change of the pointer at this time .
The specific content of the above two parts , We're going to talk a little bit about virtual heads . Old rules , Let's make an impression .
Before and after
ok, It's time to fill in the hole . As mentioned above, the linked list structure is inherently recursive , So the use of recursive solution or recursive thinking will help us to solve problems .
stay Binary tree traversal part , I talked about three popular traversal methods of binary trees , They are preorder traversal , Middle order traversal and post order traversal .
The former, the middle and the latter order actually refers to the processing order of the current node to the child node . If you process the current node first and then the child node , So that's the preface . If we deal with the left node first , Reprocessing the current node , Finally, we deal with the right node , That's the middle order traversal . Post order traversal is naturally the last to deal with the current node .
In the actual process , We're not going to buckle and die like this . such as :
def traverse(root):
print('pre')
traverse(root.left)
traverse(root.righ)
print('post')
Code above , We are both in Before entering the left and right nodes Logic , And in the After exiting the left and right nodes Logic . What kind of traversal is this ? In a general sense , I'm used to looking only at the location of the main logic , If your main logic is followed by a postorder traversal , In front of the main logic is preorder traversal . This is not the point , It doesn't help us to solve problems , What helps us a lot is what we're going to talk about .
Most of the topics are single linked lists , A single linked list has only one subsequent pointer . So there's only pre - and post - order , There is no middle order traversal .
Or take the classic inverted list mentioned above . If it's preorder traversal , Our code is like this :
def dfs(head, pre):
if not head: return pre
next = head.next
# # Main logic ( Change the pointer ) rearwards
head.next = pre
dfs(next, head)
dfs(head, None)The code for subsequent traversal is like this :
def dfs(head):
if not head or not head.next: return head
res = dfs(head.next)
# Main logic ( Change the pointer ) After entering the back node , In other words, the recursive return process will be executed to
head.next.next = head
head.next = None
return resIt can be seen that , These two kinds of writing, regardless of the boundary , Enter the reference , Or the code is not the same . Why is there such a difference ?
It's not difficult to answer this question , Just remember a very simple sentence , That's it If it's preorder traversal , So you can imagine that the list in front of you has been handled , Don't worry about how to deal with it . Accordingly If it's a subsequent traversal , Well, you can imagine that all the linked lists have been processed , Don't worry about how to deal with it . There is no doubt that this sentence is correct .
Here's the picture , It's the time of preorder traversal , What we should draw . We focused on the middle of the box ( Substructure ) That's it , At the same time, pay attention to two points .
- The front one has been dealt with
- The last one hasn't been dealt with yet

Accordingly , It's not difficult to write the following recursive code , The code comments are very detailed , Just look at the notes .
def dfs(head, pre):
if not head: return pre
# Leave your contact information ( Because none of the following has been dealt with , So you can use head.next Go to the next )
next = head.next
# Main logic ( Change the pointer ) In front of entering the back node ( Because the front has been dealt with , So there's no ring )
head.next = pre
dfs(next, head)
dfs(head, None)If it's post order traversal ? Old rules , Adhering to one of our principles , Draw a picture first .

It's not hard to see. , We can go through head.next Get the next element , And then the next element of next Point to yourself to complete the reversal .
In code, it means :
head.next.next = head
After drawing the picture , Is it easy to see that there is a ring in the diagram ? Now you know the benefits of drawing ? It's so intuitive , When you're very skilled , There's no need to draw , But before that , Please don't be lazy .
So we need to head.next Change to a value that does not cause a ring , For example, empty .

def dfs(head):
if not head or not head.next: return head
# No need to leave contact information , Because we've already walked past , There's no need to go , Now we're going back .
res = dfs(head.next)
# Main logic ( Change the pointer ) After entering the back node , In other words, the recursive return process will be executed to
head.next.next = head
# empty , To prevent the formation of rings
head.next = None
return resIt is worth noting that , Preorder traversal can easily be transformed into iteration , Therefore, it is recommended that you use preorder traversal . Let me compare the iteration above with the preorder traversal here .

So why Preorder traversal can easily be transformed into iteration Well ? actually , What I said is not accurate , To be exact, it should be Preorder traversal is easy to change to recursion without stack , And the subsequent traversal needs to be completed with the help of stack . That's not hard to understand , Since the main logic of the subsequent traversal is popped up in the function call stack , And preorder traversal doesn't need .
Here's a technique for you to write recursion , And that's to imagine that we've processed some of the data , And block them with your hands , But there's still a part to deal with , Next think ” How to deduce the data that has not been processed according to the processed data and the current data “ That's it .
Four techniques
For the above test points and points for attention , I summed up four techniques to deal with , This is a very practical skill in doing problems at ordinary times .
Virtual head
To understand the meaning of virtual heads , I'll give you a few quizzes first .
Q1: The following code ans.next What to point to ?
ans = ListNode(1)
ans.next = head
head = head.next
head = head.nextA1: At the very beginning head.
Q2: The following code ans.next What to point to ?
ans = ListNode(1)
head = ans
head.next = ListNode(3)
head.next = ListNode(4)A2: ListNode(4)
It doesn't seem difficult either , Let's move on to a problem .
Q3: The following code ans.next What to point to ?
ans = ListNode(1)
head = ans
head.next = ListNode(3)
head = ListNode(2)
head.next = ListNode(4)A3: ListNode(3)
If you get all three questions right , So congratulations , This part can be skipped .
It doesn't matter if you don't understand , I'll explain it briefly, and you can understand it .
ans.next What to point to depends on the final cut ans.next Where is the point . such as Q1,ans.next Pointing to head, We assume that the memory number it points to is 9527.
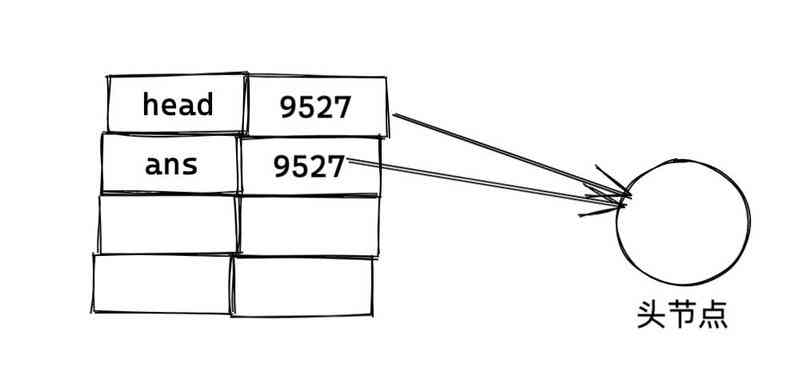
After performing head = head.next (ans and head I've been cut off ), The memory map at this point :
Let's assume that the next The memory address of the node pointed to by the pointer is 10200

It's not hard to see. ,ans It hasn't changed .
For the second example . At first, it's the same as the example above , Is directed 9527. And then it executed :
head.next = ListNode(3)
head.next = ListNode(4)ans and head At the same time, it points to ListNode(3) 了 . Pictured :

head.next = ListNode(4) It's the same thing . So the ultimate point is ans.next yes ListNode(4).
Let's look at the last one . The first half and Q2 It's the same .
ans = ListNode(1)
head = ans
head.next = ListNode(3)Follow the above analysis , here head and ans Of next All point to ListNode(3). The key is the following two lines :
head = ListNode(2)
head.next = ListNode(4)
Yes head = ListNode(2) after , head and ans And the relationship is cut off , All of the current and future head The operation will not affect ans, therefore ans It also points to the node before it was cut off , therefore ans.next The output is ListNode(3).
The reason why I spend so much time talking about this thing is , Pointer operation is the core of linked list , If you don't understand the basics , So it's hard to do . Next , We introduce the protagonist - Virtual head .
I believe that the little friends who have made the list have heard of such a name . Why is it so easy to use ? There are only two functions of it :
- Turn the head node into an intermediate node , Simplify judgment .
- By breaking links when appropriate , Return to the middle node of the list .
I mentioned above three notes on the list , One is the boundary . The head node is the most common boundary , Then if We use a virtual head to point to the head node , Virtual head is the new head node , The virtual head is not the node given by the title , Do not participate in the operation , So there's no need for special judgment , This is what virtual heads do .
If the title needs to be returned to a node in the middle of the linked list ? In fact, virtual nodes can also be used . Because of the pointer operation I mentioned above , actually , You can create a new virtual head , Then let the virtual head at the right time ( It just points to the node that needs to be returned ) disconnect , So we can go back to the virtual head next Just ok 了 .25. K A set of flip list I used this technique .
It's not just linked lists , Binary trees and so on often use this technique . For example, I want you to go back to the bottom left node of the binary tree ? We can also use the techniques mentioned above . Create a new virtual node , Virtual node next Point to the current node , And follow me , Break the link at the bottom left of the recursion , Finally back to Virtual node next Just a pointer .
Speed pointer
Determine if the list has links , And the entry of the ring can be solved by using the fast and slow pointer . I don't know. I don't know , It's not easy to forget . Not much said , You can refer to my previous question https://github.com/azl3979858... .
In addition to this , Finding the intersection point of a linked list is also a fast / slow pointer , The algorithm is similar . No, it's hard not to know , It's easy to know . And next time, it's not easy to miss or make mistakes .
In this part, please refer to my above question to solve , Write a question and you can master it . Next , Let's see because Dafa .
In addition, random access is not supported by the list , Therefore, if you want to get the middle of the array and the penultimate and other specific elements, you need some special means , And this is the speed pointer . For example, if you want to find the middle item of a linked list Make two pointers , A big step ( Two steps at a time ), One small step ( One step at a time ), So fast the pointer goes to the end , The slow pointer is just in the middle . If you ask for the last to last list 2 individual , It would be Let the quick pointer go one step first , Slow down the pointer , So fast the pointer goes to the end , The slow pointer is just the second from the bottom . This principle is not hard to understand ? This technique belongs to It's easy to , And it's not easy to forget . No, it's hard to come up with a type , So we learned to take a few questions to practice, can put down .
because
This is the second test point of the linked list - Splicing list . I am here 25. K A set of flip list ,61. Rotate the list and 92. Reverse a linked list II It's all done in this way . It's a name I've given myself , The advantage of naming is that it's easy to remember .
This method is usually not the optimal solution , But it's easy to understand , Easy to write , It's not easy to make mistakes. , It is recommended for beginners .
Take reverse linked list as an example , It's just that this time it's Reverse the middle part of the list , Then what should we do ?

We've already talked about inversion , So I suppose the list has been reversed , So how to put the inverted list together ?
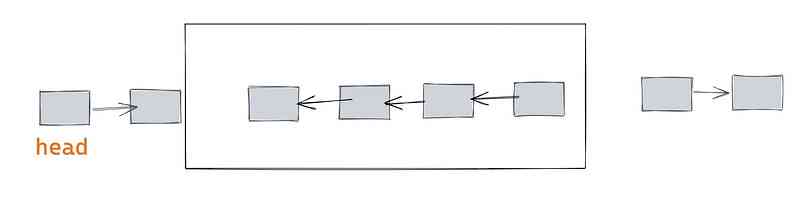
The effect we want is this :

How to achieve the effect on the picture ? My approach is to number breakpoints from the right . As shown in the figure, there are two breakpoints , There are four nodes involved . So I numbered them in turn as a,b,c,d.
Actually a,d They are the antecedents and successors of the linked list parts that need to be reversed ( Not involved in reversal ), and b and c It's the head and tail of the part that needs to be reversed ( Participate in reversal ).
So in addition to cur, Use two more pointers pre and next You can find it a,b,c,d.
It's easy when you find it , direct because .
a.next = c
b.next = d
That's good ? All I remember is 25 topic ,61 topic and 92 This is what the questions are all about , Clear, not confused .
First wear, then line up, then judge empty
This is the last of the four techniques . Although it's the last word , But that doesn't mean it doesn't matter . contrary , It has great practical value .
Let's go back to the list reversal problem mentioned above .
cur = head
pre = None
while cur != tail:
# Leave your contact information
next = cur.next
# Modify pointer
cur.next = pre
# Keep going down
pre = cur
cur = next
# After the reversal of the new head and tail node back out When to judge next Whether there is , Which of the above two lines of code should be written first ?
It's like this ?
next = cur.next
cur.next = preIt's still like this ?
cur.next = pre
next = cur.nextWear it first
My advice to you is : Wear it first . Here the wearer is modifying the pointer , Including the modification pointer of the reverse linked list and the modification pointer of the needle lead . Don't worry about the order , Wear it first .
Arrange again
After wearing it , The total number of codes has been determined , It's nothing more than permutation and combination so that the code doesn't have bug.
So the second step is to consider the order , Which of the two lines of code above comes first ? It should be first next = cur.next , The reason is that after the execution of the next statement cur.next It's changed . Because the function of the above code is to reverse , Well, in fact, it went through cur.next = pre Then the list is broken , We can't access the rest of it , That is to say, at this time you Only the head node can be returned .
actually , Yes, if there are ten lines Wear Code for , We don't have to think about it all a lot of time . We All that needs to be considered is to be changed next The part of the pointer . such as cur.next = pre Of cur Changed next. So the following is used cur.next We should consider where to put it . Other code doesn't need to be considered .
After the judgment is empty
Similar to the principle above , After wearing it , The total number of codes has been determined , Just to see which line of code will be null pointer exception .
The same technique as above , We don't have to think about it all a lot of time . We All that needs to be considered is to be changed next The part of the pointer .
Like this code
while cur:
cur = cur.nextWe consider the cur Is it empty ? It's obviously impossible , because while The conditions guarantee , So there's no need to empty .
So how is this code ?
while cur:
next = cur.next
n_next = next.nextThe code above has two next, The first one doesn't have to be empty , It's already said . And the second is needed , because next May be null. If next yes null , A null pointer exception will be thrown . So it needs to be changed to something like this :
while cur:
next = cur.next
if not next: break
n_next = next.next
These are the four tips we've given you . I believe that with these four skills , It's not so hard to write linked list questions ~ ^\_^
Topic recommendation
Finally, I recommend some questions to you , Use what you learned today to solve them ~
- 21. Merge two ordered lists
- 82. Delete duplicate elements from the sort list II
- 83. Delete duplicate elements from the sort list
- 86. Separate the list
- 92. Reverse a linked list II
- 138. Copy list with random pointer
- 141. Circular list
- 142. Circular list II
- 143. Rearrange the list
- 148. Sort list
- 206. Reverse a linked list
- 234. Palindrome list
summary
There is no big logical difference between arrays and stacks , You see, the basic operation is almost the same . If it's a single chain watch , We can't $O(1)$ Time to get the precursor node , This is why we always maintain a precursor node when traversing . But the essential reason is that the addition and deletion operations of the linked list depend on the precursor nodes . This is the basic operation of a linked list , It's the nature of the linked list .
Maybe some students have such questions ” You only talked about pointer modification and linked list splicing , Is it enough to say that the linked list can only use these ? Then how can I do the problem I will prefix and what ? Are you going to pit me ?“
I said before , At the bottom of all data structures is one or two of arrays and linked lists . And here we talk about the linked list refers to the basic operation of the list of topics . So if the topic requires you to use merge sort to merge lists , In fact, merging and sorting is no longer the scope of this article .
actually , You go buckle or something OJ Turn over the list questions, you will find that most of their linked list questions refer to the reference list , And you need to do some operations on the linked list . For example, most of the questions about trees are trees , The title you need to search on the tree . In other words, you need to operate the tree ( For example, modify the pointer of the tree ) There are very few topics for , For example, there is a question that asks you to add a right The pointer , Pointer to the right of the peer , If it's on the far right , Then it points to empty .
The basic operation of the linked list is to add, delete and check , Keep in mind that the basic operation and complexity of linked list is the basis of solving problems . These are not enough , You should remember my formula ” One principle , Two test sites , Three notes , Four techniques “.
Do a list of questions , To get started , Without it , Only picture tour . Can draw a picture , And you can get started by following the diagram , No matter whether you write code or not bug .
And the core of the title of the linked list has only two inspection points , One is pointer operation , It's a typical reversal . The other is the splicing of linked lists . These two are the essence of linked lists , It's also the main test site .
I know that the examination site is not enough , Where we write code is prone to mistakes ? What to pay attention to ? Here I've listed three common mistakes , The difference is the ring , Boundary and sequence .
Ring refers to the mutual reference between nodes , If the title itself has a ring , 90 % Double pointer can solve this problem , If there is no ring in itself , So the ring is what we left when we manipulate the pointer . How to solve the problem of ring ? That's it drawing , Then focus on the substructure , Ignore other information .
Except for the rings , Another mistake is often the boundary conditions , And the judgment of the chain head of the boundary is a big head . Overcome this , We need to read the questions carefully , Look at the requirements of the topic and the return value , Another useful technique is virtual nodes .
If you use the recursive method to solve the list of questions , Be sure to write a preface or a preface .
- If it's a preface , that Just think about substructures , The front one has been dealt with , How to deal with , Never mind . I have to ask , That's the same way . There is no need to consider how to deal with the latter , I have to ask , That's the same way
- If it's a follow-up , that Just think about substructures , The rest has been dealt with , How to deal with , Never mind . I have to ask , That's the same way . There is no need to think about how to deal with the former . I have to ask , That's the same way
If you want to write both recursion and iteration , I recommend that you use preorder traversal . Because preorder traversal is easy to change to recursion without stack .
That's all about the linked list topic . What do you think of this , Welcome to leave a message , I'll check the answers one by one whenever I have time . More algorithmic routines can access my LeetCode Solution warehouse :https://github.com/azl3979858... . At present already 37K star La . You can also pay attention to my official account. 《 Force buckle plus 》 Take you to gnaw the hard bone of algorithm .
I sorted it out 1000 Multi page e-books have been developed and downloaded , You can go to my official account 《 Force buckle plus 》 Background reply e-book to get .