当前位置:网站首页>AcWing 346. Solution to the problem of water splashing festival in the corridor (deduction formula, minimum spanning tree)
AcWing 346. Solution to the problem of water splashing festival in the corridor (deduction formula, minimum spanning tree)
2022-07-07 01:36:00 【Mr. Qiao Da】
AcWing 346. Corridor Water Splashing Festival
The key to solving the problem is to deduce the formula :**(Size[a] * Size[b] - 1) * (w + 1)** The meaning of this formula is mortgage : Traverse to two points belonging to two different connected blocks connected by a certain edge , Connect all points of the two connecting blocks to each other , Subtract an existing edge , After introducing the formula , Traverse all edges according to the algorithm of minimum spanning tree , Find out two points that are not in a connected block and accumulate the calculated value with a formula
#include<bits/stdc++.h>
using namespace std;
const int N = 6010;
struct Edge{
int a, b, w;
bool operator< (const Edge &t) const {
return w < t.w;
}
}e[N * 4];
int T, n, m;
int p[N];
int Size[N];
int find(int x){
if(x != p[x]) p[x] = find(p[x]);
return p[x];
}
int main()
{
cin>>T;
while(T -- ){
cin>>n;
int res = 0;
for(int i = 0; i < n - 1; i ++ ){
int a, b, w;
cin>>a>>b>>w;
e[i] = {
a, b, w};
}
// Initialize and query array
for(int i = 1; i <= n; i ++ ){
p[i] = i;
Size[i] = 1;
}
sort(e, e + n - 1);
for(int i = 0; i < n - 1; i ++ ){
int a = find(e[i].a), b = find(e[i].b), w = e[i].w;
if(a != b){
res += (Size[a] * Size[b] - 1) * (w + 1); // The formula , Connect all points of the two connecting blocks to each other , Subtract an existing edge
p[a] = b;
Size[b] += Size[a];
}
}
cout<<res<<endl;
}
return 0;
}
边栏推荐
- Comparison of picture beds of free white whoring
- Can the system hibernation file be deleted? How to delete the system hibernation file
- 分享一个通用的so动态库的编译方法
- Today's question -2022/7/4 modify string reference type variables in lambda body
- Neon Optimization: an optimization case of log10 function
- mysqlbackup 还原特定的表
- THREE.AxesHelper is not a constructor
- Yunna - work order management system and process, work order management specification
- 增加 pdf 标题浮窗
- HMM 笔记
猜你喜欢
Make Jar, Not War

如何管理分布式团队?
微信公众号发送模板消息
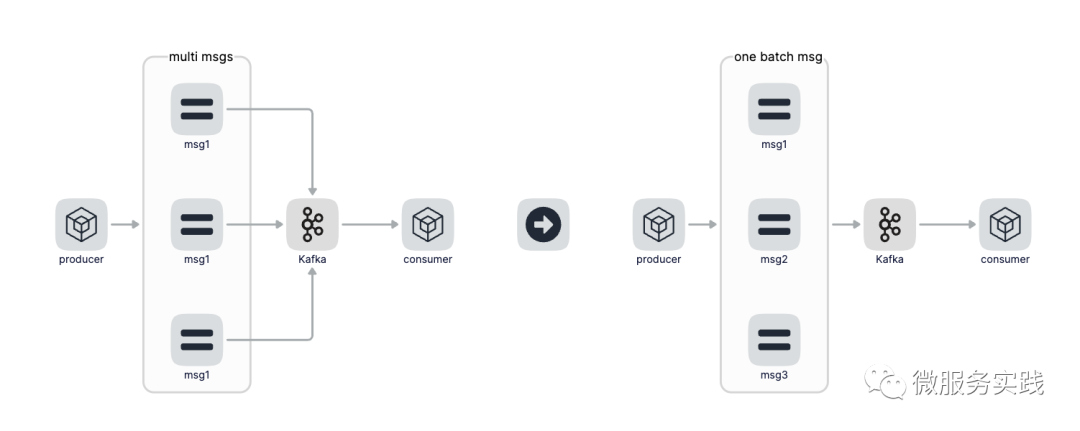
Go zero micro service practical series (IX. ultimate optimization of seckill performance)
According to the analysis of the Internet industry in 2022, how to choose a suitable position?
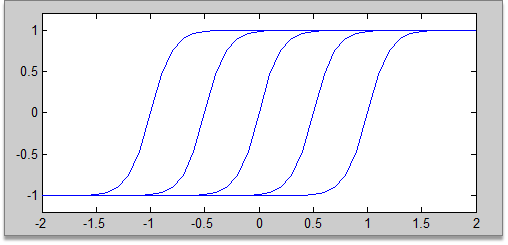
一起看看matlab工具箱内部是如何实现BP神经网络的
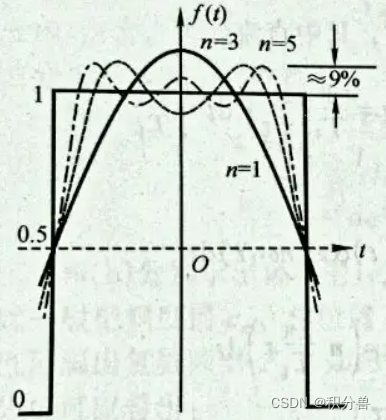
【信号与系统】
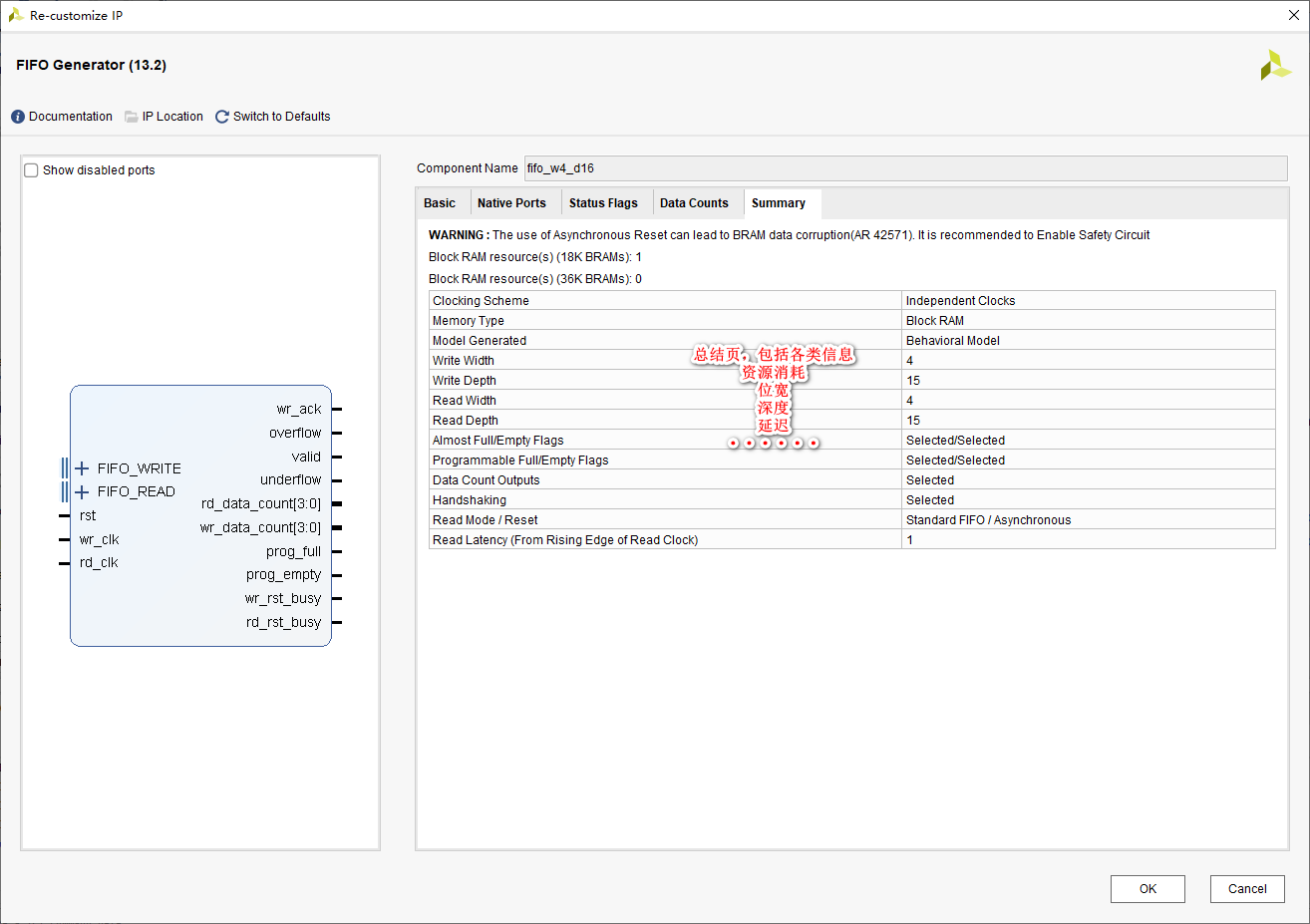
Start from the bottom structure to learn the customization and testing of fpga---- FIFO IP

Let's see how to realize BP neural network in Matlab toolbox

Dark horse notes - exception handling
随机推荐
拖拽改变顺序
C language instance_ three
LeetCode. 剑指offer 62. 圆圈中最后剩下的数
Set up [redis in centos7.x]
Realize incremental data synchronization between MySQL and ES
POJ 3177 Redundant Paths POJ 3352 Road Construction(双连接)
长按按钮执行函数
Failed to successfully launch or connect to a child MSBuild. exe process. Verify that the MSBuild. exe
Body mass index program, entry to write dead applet project
shell脚本快速统计项目代码行数
Typical problems of subnet division and super network construction
机器学习:随机梯度下降(SGD)与梯度下降(GD)的区别与代码实现。
2022 Google CTF SEGFAULT LABYRINTH wp
HMM notes
公钥\私人 ssh避password登陆
黑马笔记---异常处理
dvajs的基础介绍及使用
taro3.*中使用 dva 入门级别的哦
Neon Optimization: summary of performance optimization experience
Match VIM from zero (0) -- Introduction to vimscript