AcWing 1148. 秘密的牛奶运输 题解（最小生成树）

AcWing 1148. 秘密的牛奶运输
解题思路：先找到最小生成树，计算出权值之和并标记所有最小生成树内的边。之后遍历所有边，找到包含两个点的路径的上的最大边和次大边并记录，（当两个点找到一条新的路径相连时，只有断开哪个最大边（t = sum - dist1[a][b] + w，dist1是最大边，得出的t才会是更小值，才能得出次小生成树），才能保证找到的是次小生成树，所以要记录最大边，记录次大边是为了防止最大边已经被用过），之后遍历所有非最小生成树内的边，依次替换树内的边，最终找到次小生成树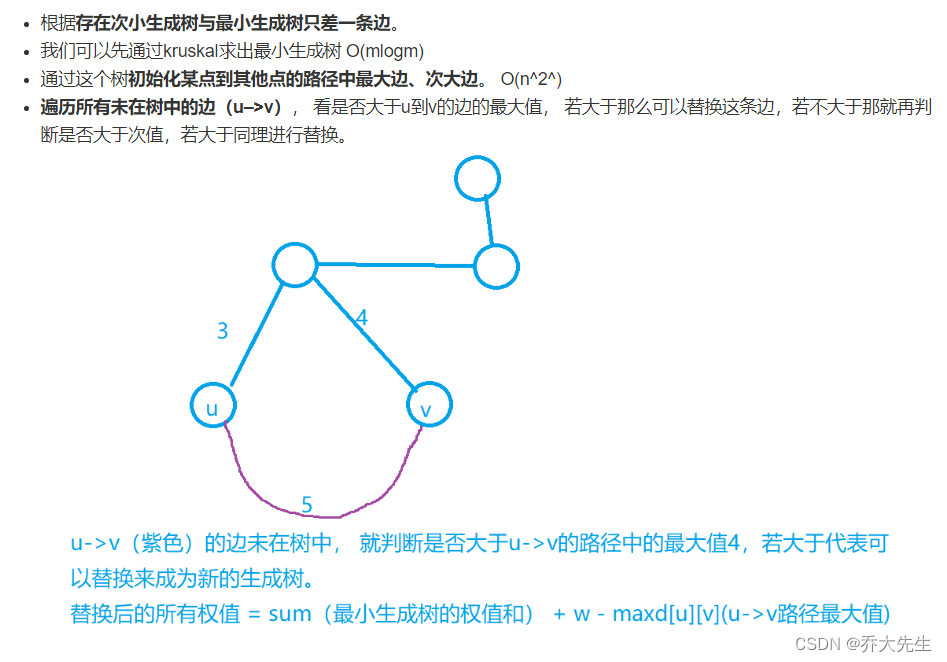

大佬题解原地址

#include<bits/stdc++.h>

using namespace std;

typedef long long ll;

const int N = 510, M = 2e4 + 10;

int n, m;
int p[N];  //并查集 
int dist1[N][N], dist2[N][N];  //分别记录对应边路径上的最大值和次大值
ll res = 1e18;  //最终答案 
ll sum;  // 记录最小生成树的权值
int h[N], e[M], ne[M], w[M], idx;  //记录树 

struct Edge{
    
	int a, b, w;
	bool f;  //标记这个边是否在最小生成树内 
	bool operator< (const Edge &t) const {
    
		return w < t.w;
	}
}edg[M];

void add(int a, int b, int c){
    
	e[idx] = b;
	ne[idx] = h[a];
	w[idx] = c;
	h[a] = idx ++ ;
} 

int find(int x){
    
	if(x != p[x]) p[x] = find(p[x]);
	return p[x];
}

void dfs(int u, int fa, int mad1, int mad2, int d1[], int d2[]){
      //找到每个点对应路径上个最大值和次大值 
	d1[u] = mad1, d2[u] = mad2;  //d1、d2数组在此之前没有赋值 
	for(int i = h[u]; ~i; i = ne[i]){
    
		int j = e[i];
		if(j != fa){
    
			int td1 = mad1, td2 = mad2;
			if(w[i] > td1){
    
				td2 = td1;
				td1 = w[i];
			}
			else if(w[i] < td1 && w[i] > td2){
    
				td2 = w[i];
			}
			dfs(j, u, td1, td2, d1, d2);
		}
	} 
}

signed main()
{
    
	cin>>n>>m;
	memset(h, -1, sizeof h);
	for(int i = 0; i < m; i ++ ){
    
		int a, b, c;
		cin>>a>>b>>c;
		edg[i] = {
    a, b, c};
	}
	
	//找到最小生成树 
	sort(edg, edg + m);
	for(int i = 1; i <= n; i ++ ) p[i] = i;
	
	for(int i = 0; i < m; i ++ ){
    
		int a = edg[i].a, b = edg[i].b, w = edg[i].w;  //这里要利用点去建图，所以a、b均用于表示自己 
		int pa = find(a), pb = find(b);
		if(pa != pb){
    
			sum += w;
			p[pa] = pb;
			add(a, b, w);
			add(b, a, w);
			edg[i].f = true; 
		}
	}
	
	//找到每个点对应路径的最大值和次大值
	for(int i = 1; i <= n; i ++ ) dfs(i, -1, -1e9, -1e9, dist1[i], dist2[i]);
	
	for(int i = 0; i < m; i ++ ){
    
		if(!edg[i].f){
    
			int a = edg[i].a, b = edg[i].b, w = edg[i].w;
			ll t;
			if(w > dist1[a][b]){
    
				t = sum - dist1[a][b] + w;
			}
			else if(w > dist2[a][b]){
    
				t = sum - dist2[a][b] + w;
			}
			res = min(res, t);
		}
	} 
	cout<<res<<endl;
	return 0;
}