LeetCode. 剑指offer 62. 圆圈中最后剩下的数

题目描述

0,1,···,n-1这n个数字排成一个圆圈，从数字0开始，每次从这个圆圈里删除第m个数字（删除后从下一个数字开始计数）。求出这个圆圈里剩下的最后一个数字。

例如，0、1、2、3、4这5个数字组成一个圆圈，从数字0开始每次删除第3个数字，则删除的前4个数字依次是2、0、4、1，因此最后剩下的数字是3。

思路

这是一个著名的数学问题 —— 约瑟夫环。

这里直接贴出解法（没有严格的数学证明，但比较容易理解和记忆）

用时光倒流法，从最后的情况开始，往回推。

借用一位大佬的图：

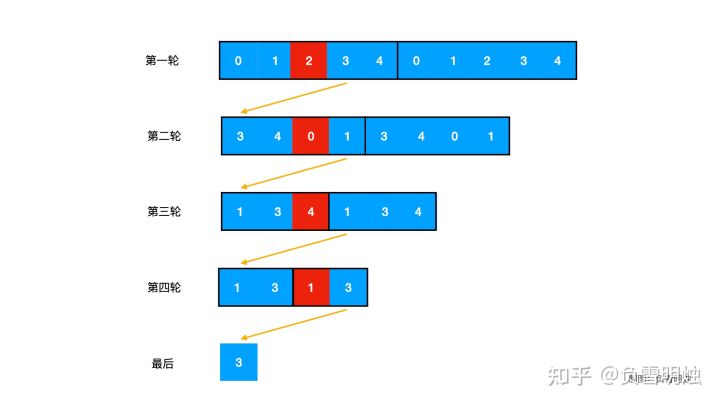
• 最后一轮（称之为第n轮），只剩一个数字（称之为x）时，数组总大小为1，x的下标为0
• n-1轮中，x是安全的，我们把整个环拉成一条无限长的直线，则容易知道，这一轮的起点，到x，有m个数，即x前面有m个数，且这一轮中移除的是x前面的那个数。那么该轮中x的下标为(m + 0) % 2（在x前面补上m个数），由于有环，我们取个模。这一轮保留了2个数。
• n-2轮中，上一轮的第一个数被保留了下来，说明n-1轮的第一个数前面有m个数，且该轮移除的是这个数前面的那个数。则在整个数组前面补上m个数，则n-1轮中所有数的下标都要往右移m，所以该轮中x的下标为，(((m + 0) % 2) + m) % 3
• …
• 第1轮，还原到初始状态，就能求出x在初始轮中的下标

class Solution {
    
    public int lastRemaining(int n, int m) {
    
        // 最后一轮的下标
        int x = 0;
        for (int i = 2; i <= n; i++) {
    
            x = (x + m) % i;
        }
        return x;
    }
}

公式为：$f(n,m)=[f(n-1,m)+m]$，边界条件为 $f(1,m)=0$

严谨的数学推导，参考：这或许是你能找到的最详细约瑟夫环数学推导！ - 知乎