当前位置:网站首页>7.6模拟赛总结
7.6模拟赛总结
2022-07-06 17:34:00 【Flame*】
咕咕咕咕咕
我以为会过一车人
我因为人均170+
我有点意外
时间安排
7.30-9.00
看了看题 感觉T1显然状压 T2差不多会50 T3只会n^2 想了半天T2有什么别的做法 感觉都单调性 但是没有抓住这个想法
先打了T2暴力
9.00-10.00
感觉不太行 又想了一会T3 也没啥想法
然后打了T3的暴力
10.00-10.40
打了T1的暴力 想了一会 觉得T1的第二档是不是有什么神秘做法(因为是图) 感觉有点树形dp那味 但是不是很会
10.40-12.00
重新回想T1 反应过来可以分块掏决策单调性
然后努力回想怎么维护区间逆序数 这里我犯了一个错误 因为之前听了noi那个题 就觉得区间逆序数很复杂(实际上赛场推出来了) 推出来之后还觉得有点不明所以 (其实是因为noi那个题既有区间也有值域限制)
最后时间不够了(剩了20分钟 ) 就检查一下交题了
题目分析
T1
f [ S , o p 1 , p o s , o p 2 ] f[S,op1,pos,op2] f[S,op1,pos,op2] 当前走过的点的状态为 S S S 是否在终点的状态为 o p 1 op1 op1 在点 p o s pos pos 上 上一条走过的边的状态是 o p 2 op2 op2
转移分情况考虑
正常模拟转移
o p 1 = 0 op1=0 op1=0 的时候走到了一个标记点:可以考虑转成 o p 1 = 1 op1=1 op1=1 加上贡献
o p 1 = 1 op1=1 op1=1 枚举一个没走过的标记点作为新起点 同时向 o p 2 = 1 / 0 op2=1/0 op2=1/0 转移
貌似我更擅长做状压dp一点
T2
f [ i ] f[i] f[i] 表示最后一段分到 i i i 的最小代价
可以注意到 代价就是区间逆序对 再考虑每填入一个数 前面不同位置 从小到大 增加的值是不增的 形如 5554444321111... 5 5 5 4 4 4 4 3 2 1 1 1 1... 5554444321111...(值改变的位置就是出现了一个比它大的数)
然后可以 n 2 n^2 n2 做
基于这个性质 可以证明决策单调性
所以有了 n l o g n n nlogn~\sqrt n nlogn n 的决策单调性套分块做法
upd
正解是cdq套分治决策单调性+类似莫队方法 维护两个指针 暴力跳区间逆序对
之所以需要cdq套一下 是因为分治决策单调性需要内容之间没有依赖 而这个有依赖 所以通过cdq分治搞出前面的dp值
T3
这个是真不会 只想了n^2或者撒点
边栏推荐
- 斗地主游戏的案例开发
- table表格设置圆角
- Metauniverse urban legend 02: metaphor of the number one player
- What kind of experience is it to realize real-time collaboration in jupyter
- gnet: 一个轻量级且高性能的 Go 网络框架 使用笔记
- Receive user input, height BMI, BMI detection small business entry case
- Neon Optimization: performance optimization FAQ QA
- golang中的WaitGroup实现原理
- 接收用户输入,身高BMI体重指数检测小业务入门案例
- 【案例分享】网络环路检测基本功能配置
猜你喜欢

「精致店主理人」青年创业孵化营·首期顺德场圆满结束!

Maidong Internet won the bid of Beijing life insurance to boost customers' brand value
2022 Google CTF SEGFAULT LABYRINTH wp

字节P7专业级讲解:接口测试常用工具及测试方法,福利文
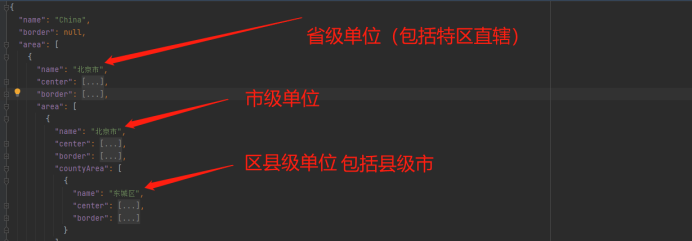
Provincial and urban level three coordinate boundary data CSV to JSON
![[牛客] [NOIP2015]跳石头](/img/9f/b48f3c504e511e79935a481b15045e.png)
[牛客] [NOIP2015]跳石头

迈动互联中标北京人寿保险,助推客户提升品牌价值
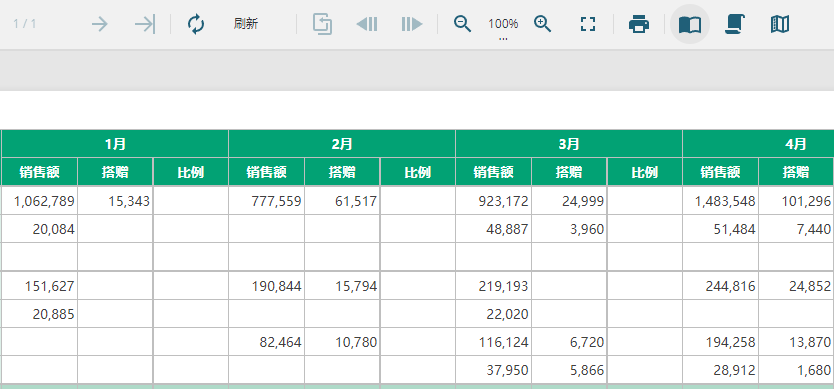
Activereportsjs 3.1 Chinese version | | | activereportsjs 3.1 English version
Build your own website (17)
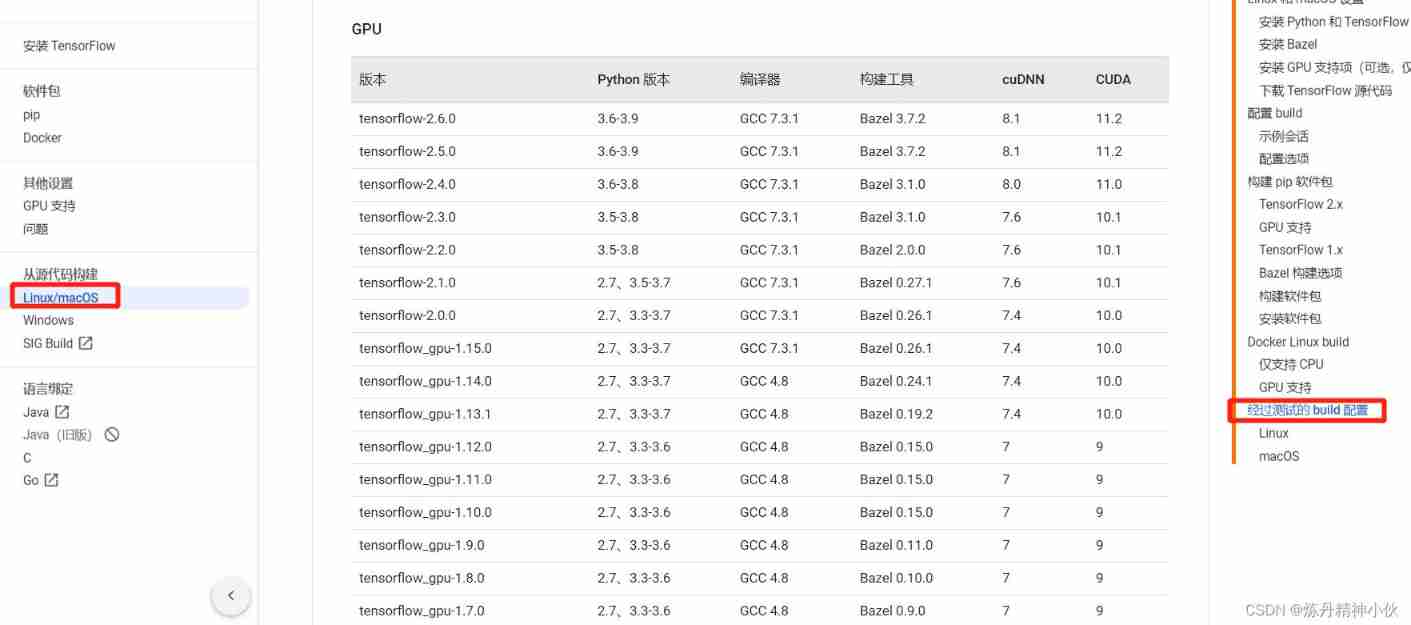
Tensorflow GPU installation
随机推荐
深度学习框架TF安装
How do novices get started and learn PostgreSQL?
golang中的atomic,以及CAS操作
MySQL script batch queries all tables containing specified field types in the database
Receive user input, height BMI, BMI detection small business entry case
Windows installation mysql8 (5 minutes)
Implementation principle of waitgroup in golang
mysql: error while loading shared libraries: libtinfo.so.5: cannot open shared object file: No such
[hfctf2020]babyupload session parsing engine
Neon Optimization: an instruction optimization case of matrix transpose
[Niuke] b-complete square
Make a simple graphical interface with Tkinter
Oracle:CDB限制PDB资源实战
The MySQL database in Alibaba cloud was attacked, and finally the data was found
Mongodb client operation (mongorepository)
Analysis of mutex principle in golang
Openjudge noi 1.7 08: character substitution
Transformation transformation operator
Address information parsing in one line of code
Grc: personal information protection law, personal privacy, corporate risk compliance governance