当前位置:网站首页>动态规划思想《从入门到放弃》
动态规划思想《从入门到放弃》
2022-07-06 17:16:00 【rabbit_zli】
动态规划的定义
将原问题拆解成若干子问题 ,同时保存子问题的答案,使得每个子问题只求解一次,最终获得原问题的答案。
动态规划的一般流程
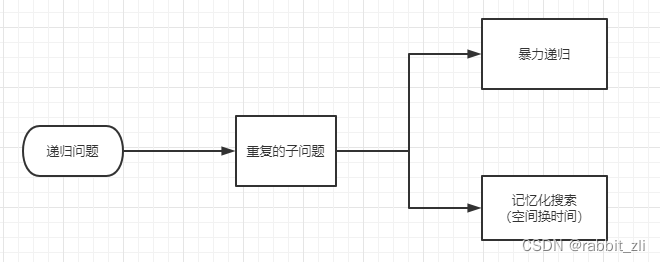
例子1:一维空间的动态规划
题目:求斐波那契数列
- 暴力递归解决
// 使用递归解决
int fibonacci(int i) {
return i <= 1 : i : fibonacci(i - 1) + fibonacci(i - 2);
}
暴力递归的时间复杂度是指数级,我们需要使用记忆化搜索去解决这个问题
- 记忆化搜索(动态规划思想)
// 使用动态规划思想 记忆化搜索
int fibonacci(int fib) {
// 定义一个数组 存储第N项的斐波那契数
int[] cache = new int[fib + 1];
// 遍历
for (int i = 0; i < cache.length; i++) {
if (fib <= 1) {
cache[i] = i;
continue;
}
cache[i] = cache[i - 2] + cache[i - 1];
}
return cache[fib];
}
复杂的动态规划
复杂的动态规划:
- 维度变化了 有可能是二维或三维空间;
- 中间可能会有取舍最优子结构
题目2:不同路径
题目描述:一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?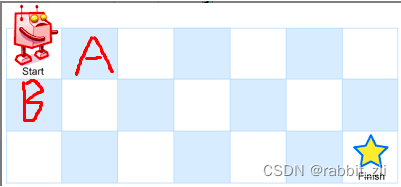
对于上述问题,由于每次只能 向右或向下 走,于是我们可以转变为子问题:
子问题1:对于A如何走到右下角
子问题2:对于B如何走到右下角
所以总共的走法就等于 【A】的子问题的解+【B】的子问题的解
- 解法一:使用常规的递归解法
// 使用递归的解法
int paths(int m, int n) {
// 定义一个二维网格
int[][] table = new int[m][n];
// 调用递归函数
return dfs(table, 0, 0);
}
int dfs(int[][] table, int row, int col) {
// 递归终止条件
// 1.1 处理边界值
if (row < 0 || row >= table.length || col < 0 || col >= table[0].length) {
return 0;
}
// 1.2 若走到目的地 则返回1
if (row == table.length - 1 && col == table[0].length - 1) {
return 1;
}
// 转换成子问题的解
return dfs(table, row + 1, col) + dfs(table, row, col + 1);
}
- 解法二:记忆化搜索
/** 使用动态规划思想解决 可以发现 每一格的路径数量是由其上一格和左边一格的路径总数决定的 */
int paths(int m, int n) {
// 定义一个二维矩阵
int[][] table = new table[m][n];
// 先初始化第一行和第一列
for (int i = 0; i < m; i++) {
table[m][0] = 1;
}
for (int i = 0; i < n; i++) {
table[0][n] = 1;
}
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
table[i][j] = table[i - 1][j] + table[i][j - 1];
}
}
return table[m - 1][n - 1];
}
边栏推荐
- Data processing of deep learning
- Deeply explore the compilation and pile insertion technology (IV. ASM exploration)
- Configuring the stub area of OSPF for Huawei devices
- 随时随地查看远程试验数据与记录——IPEhub2与IPEmotion APP
- Building a dream in the digital era, the Xi'an station of the city chain science and Technology Strategy Summit ended smoothly
- Dell筆記本周期性閃屏故障
- Leetcode(547)——省份数量
- 深度学习简史(一)
- [Batch dos - cmd Command - Summary and Summary] - String search, find, Filter Commands (FIND, findstr), differentiation and Analysis of Find and findstr
- stm32F407-------SPI通信
猜你喜欢

Installation and testing of pyflink
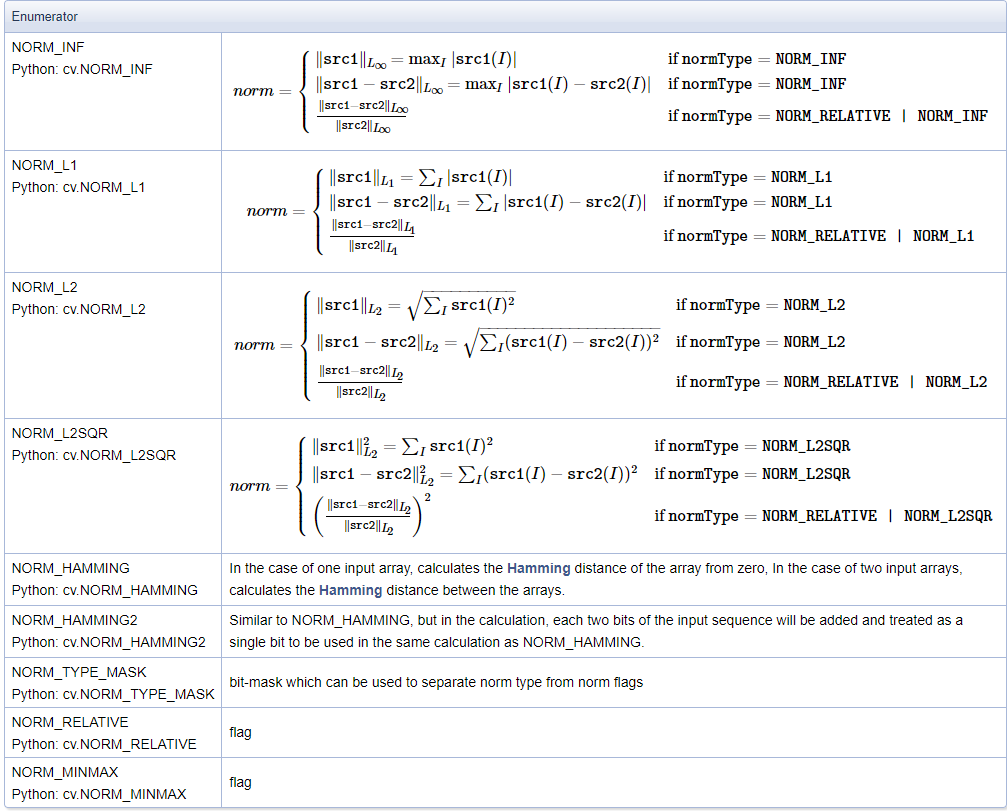
详解OpenCV的矩阵规范化函数normalize()【范围化矩阵的范数或值范围(归一化处理)】,并附NORM_MINMAX情况下的示例代码

随时随地查看远程试验数据与记录——IPEhub2与IPEmotion APP

View remote test data and records anytime, anywhere -- ipehub2 and ipemotion app

Batch obtain the latitude coordinates of all administrative regions in China (to the county level)
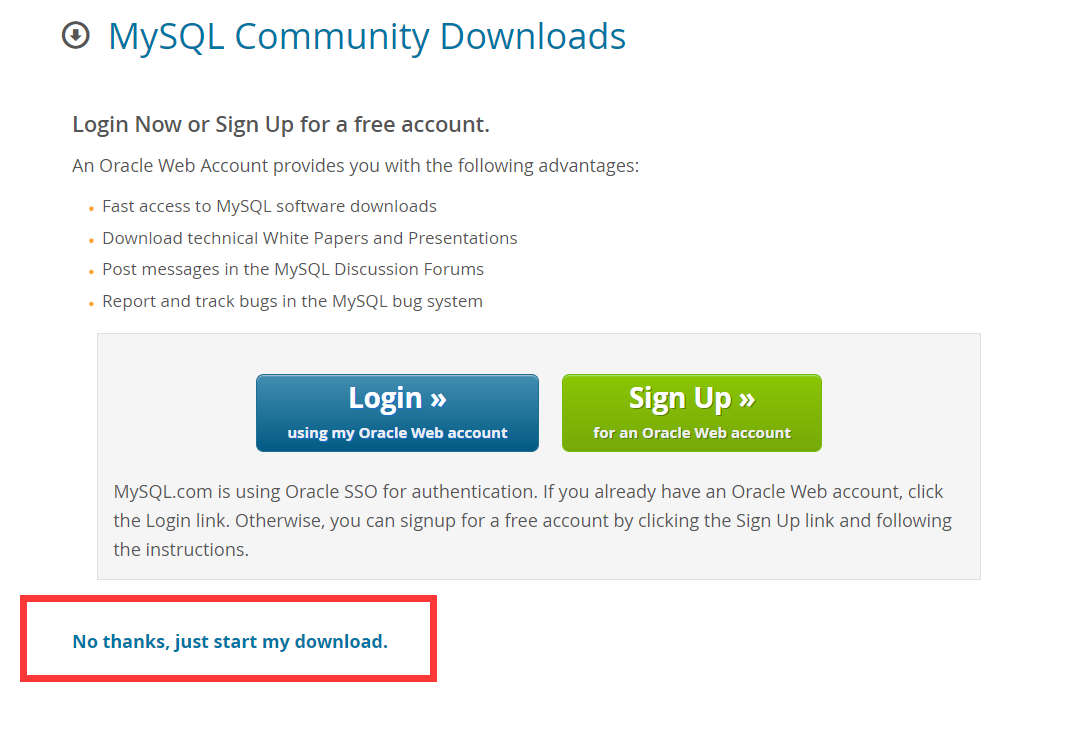
windows安装mysql8(5分钟)
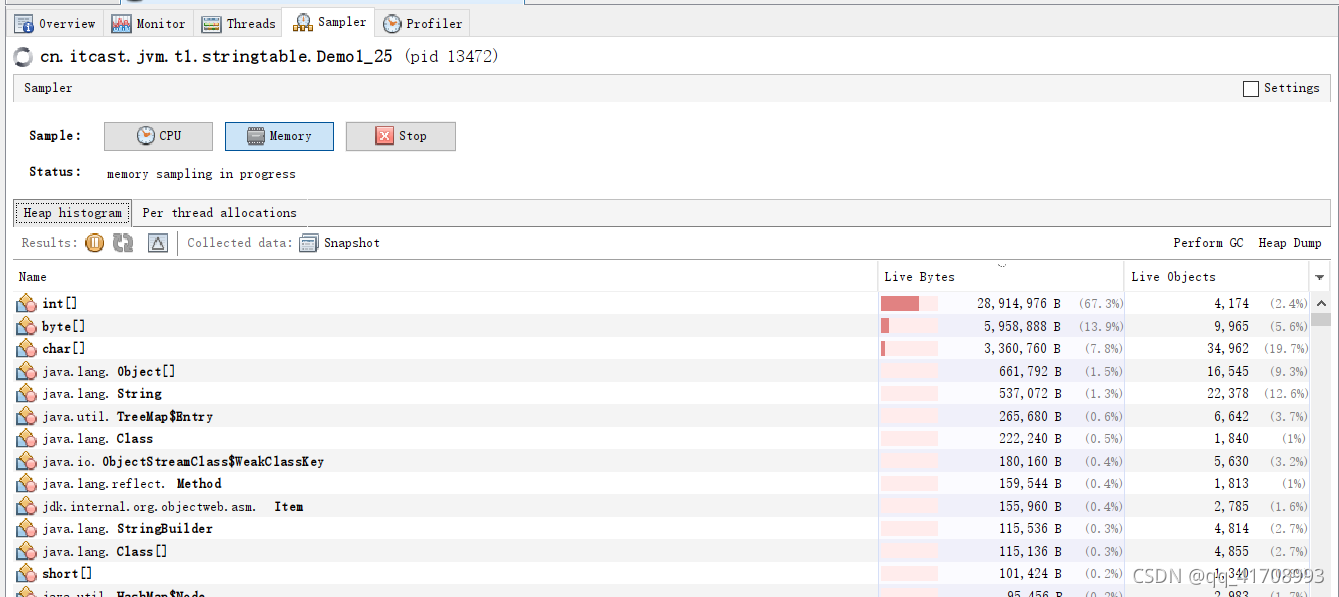
【JVM调优实战100例】04——方法区调优实战(上)
建立自己的网站(17)
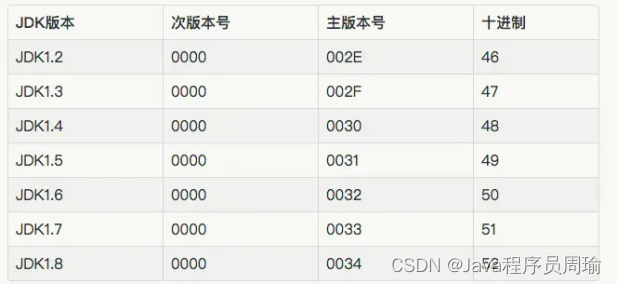
. Bytecode structure of class file
![[user defined type] structure, union, enumeration](/img/a5/d6bcfb128ff6c64f9d18ac4c209210.jpg)
[user defined type] structure, union, enumeration
随机推荐
Notes of training courses selected by Massey school
What is time
【批处理DOS-CMD命令-汇总和小结】-字符串搜索、查找、筛选命令(find、findstr),Find和findstr的区别和辨析
Chenglian premium products has completed the first step to enter the international capital market by taking shares in halber international
迈动互联中标北京人寿保险,助推客户提升品牌价值
Learning notes 5: ram and ROM
Advanced learning of MySQL -- basics -- multi table query -- inner join
深度学习之环境配置 jupyter notebook
【批處理DOS-CMD命令-匯總和小結】-字符串搜索、查找、篩選命令(find、findstr),Find和findstr的區別和辨析
筑梦数字时代,城链科技战略峰会西安站顺利落幕
Levels - UE5中的暴雨效果
threejs图片变形放大全屏动画js特效
Zabbix 5.0:通过LLD方式自动化监控阿里云RDS
stm32F407-------DAC数模转换
Linear algebra of deep learning
windows安装mysql8(5分钟)
Learn to use code to generate beautiful interface documents!!!
ZABBIX 5.0: automatically monitor Alibaba cloud RDS through LLD
Mujoco second order simple pendulum modeling and control
Zynq transplant ucosiii