1123. 最深叶节点的最近公共祖先

1123. 最深叶节点的最近公共祖先

给你一个有根节点 root 的二叉树，返回它 最深的叶节点的最近公共祖先 。

回想一下：

叶节点 是二叉树中没有子节点的节点
树的根节点的 深度 为 0，如果某一节点的深度为 d，那它的子节点的深度就是 d+1
如果我们假定 A 是一组节点 S 的 最近公共祖先，S 中的每个节点都在以 A 为根节点的子树中，且 A 的深度达到此条件下可能的最大值。

示例 1：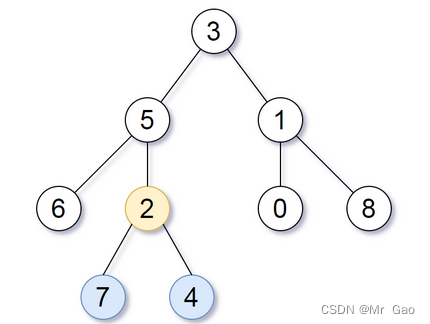

输入：root = [3,5,1,6,2,0,8,null,null,7,4]
输出：[2,7,4]
解释：我们返回值为 2 的节点，在图中用黄色标记。
在图中用蓝色标记的是树的最深的节点。
注意，节点 6、0 和 8 也是叶节点，但是它们的深度是 2 ，而节点 7 和 4 的深度是 3 。

示例 2：

输入：root = [1]
输出：[1]
解释：根节点是树中最深的节点，它是它本身的最近公共祖先。

示例 3：

输入：root = [0,1,3,null,2]
输出：[2]
解释：树中最深的叶节点是 2 ，最近公共祖先是它自己。

/** * Definition for a binary tree node. * struct TreeNode { * int val; * struct TreeNode *left; * struct TreeNode *right; * }; */
 #define size 100
 int f(struct TreeNode* root){
    
     if(root){
    
         int a=f(root->left)+1;
         int b=f(root->right)+1;
         if(a>b){
    
             return a;
         }
         return b;
     }
     else{
    
         return 0;
     }
     
 }


struct TreeNode* lcaDeepestLeaves(struct TreeNode* root){
    
    struct TreeNode *queue[size],*p;
      struct TreeNode *re=NULL;
    int front,rear;
    int h=f(root);
    front=0;
    rear=0;
    queue[rear]=root;
    rear=(rear+1)%size;
     queue[rear]=NULL;
    rear=(rear+1)%size;
    printf("h %d ",h);
    int hz=1;
    if(h==1){
    
        re=root;
    }
    while(front!=rear){
    
        p=queue[front];
      
        front=(front+1)%size;
        if(p==NULL&&front!=rear){
    
            hz++;
             queue[rear]=NULL;
             rear=(rear+1)%size;
             printf("hz %d ",hz);
        }
        else{
    
            if(rear==front){
    
                break;
            }
              printf("%d |",p->val);
            if(hz==h-1){
    
                if(p->left&&p->right){
    
                    re=p;
                }
                if(p->right&&p->left==NULL){
    
                    re=p->right;
                }
                if(p->left&&p->right==NULL){
    
                    re=p->left;
                }
            }

            if(p->left){
    
                 queue[rear]=p->left;
                 rear=(rear+1)%size;
            }
            if(p->right){
    
                 queue[rear]=p->right;
                 rear=(rear+1)%size;
            }
        }
        
    }
    return re;

}

下面这个方法应该更好
1.判断当前节点左右孩子的深度，相等则当前节点为最近公共祖先；
2.左孩子深度大于右孩子深度则公共祖先则必在左子树上；
3.左孩子深度小于右孩子深度则公共祖先则必在右子树上；
遍历树找到一个左右子树深度相等的节点即可。

/** * Definition for a binary tree node. * struct TreeNode { * int val; * struct TreeNode *left; * struct TreeNode *right; * }; */
int getDepth(struct TreeNode* root){
    
    if(!root)return 0;
    return fmax(getDepth(root->left),getDepth(root->right))+1;
}

struct TreeNode* lcaDeepestLeaves(struct TreeNode* root){
    
    struct TreeNode* res=root,*cur=root;
    while(cur){
    
        int left=getDepth(cur->left);
        int right=getDepth(cur->right);
        if(left==right){
    
            res=cur;
            break;
        }else if(left>right){
    
            cur=cur->left;
        }else cur=cur->right;
    }
    return res;
}