当前位置:网站首页>BFS realizes breadth first traversal of adjacency matrix (with examples)
BFS realizes breadth first traversal of adjacency matrix (with examples)
2022-07-07 00:59:00 【Demo Dragon】
1. The establishment of adjacency matrix
#include<iostream>
using namespace std;
#include<queue>
#include<stdbool.h>
// Creation of adjacency matrix
typedef char vextype;// Vertex type customization
typedef int edgetype;// Custom weights on the edge
#define MAXVEX 100// Maximum number of vertices
#define MAXS 66666// Represents infinity
typedef struct
{
vextype vexs[MAXVEX];// Vertex table
edgetype arc[MAXVEX][MAXVEX];// Adjacency matrix
int numNodes;// Current number of vertices
int numEdges;// Current number of sides
}MGraph;
1. The adjacency matrix representation of undirected network graph is established by reference
//1. The adjacency matrix representation of undirected network graph is established by reference
void CreatGraph(MGraph& G)
{
cout << " Please enter the number of vertices and edges :";
cin >> G.numNodes >> G.numEdges;
cout << " Please enter all vertex information :" << endl;
for (int i = 0; i < G.numNodes; i++)
cin >> G.vexs[i];
for (int i = 0; i < G.numNodes; i++)
for (int j = 0; j < G.numNodes; j++)
G.arc[i][j] = 0;
cout << " Please enter the edges composed of vertices and their weights :" << endl;
for (int i = 0; i < G.numEdges; i++)
{
int w, m, n;
cin >> m >> n >> w;
G.arc[m][n] = w;
G.arc[n][m] = G.arc[m][n];
}
}
2. The pointer establishes the adjacency matrix representation of undirected network graph
//2. The pointer establishes the adjacency matrix representation of undirected network graph
void CreatGraph(MGraph* G)
{
cout << " Please enter the number of vertices and edges :";
cin >> G->numNodes >> G->numEdges;
cout << " Please enter all vertex information :" << endl;
for (int i = 0; i < G->numNodes; i++)
cin>>G->vexs[i];
for (int i = 0; i < G->numNodes; i++)
for (int j = 0; j < G->numNodes; j++)
G->arc[i][j] = 0;
cout << " Please enter the edges composed of vertices and their weights :" << endl;
for (int i = 0; i < G->numEdges; i++)
{
int w, m, n;
cin >> m >> n >> w;
G->arc[m][n] = w;
G->arc[n][m] = G->arc[m][n];
}
}
2. Print adjacency matrix
// Print adjacency matrix
void PrintGraph(MGraph G)
{
int len = G.numNodes;
for (int i = 0; i < len; i++)
{
for (int j = 0; j < len; j++)
{
cout << G.arc[i][j] << " ";
}
cout << endl;
}
}
3. Depth first recursive algorithm of adjacency matrix
//3. Depth first recursive algorithm of adjacency matrix
#define MAXVEX 100
int visit[MAXVEX] = {
0 };
void DFS(MGraph G, int i)
{
cout << G.vexs[i] << " ";
visit[i] = 1;
for (int j = 0; j < G.numNodes; j++)
{
if (!visit[j] && G.arc[i][j] != 0)
{
DFS(G, j);
}
}
}
void DFST(MGraph G)
{
for (int i = 0; i < G.numNodes; i++)
visit[i] = 0;
for (int i = 1; i < G.numNodes; i++)
{
if(!visit[i])
DFS(G, i);
}
}
4. Breadth first traversal algorithm of adjacency matrix
// Breadth first traversal algorithm of adjacency matrix
void BFS(MGraph G)
{
queue<vextype> Q;
for (int i = 0; i < G.numNodes; i++)
visit[i] = 0;
for (int i = 0; i < G.numNodes; i++){
if (!visit[i]){
visit[i] = 1;
cout << G.vexs[i] << " ";
Q.push(i);
while (!Q.empty()){
Q.pop();
for (int j = 0; j < G.numNodes; j++)
if (G.arc[i][j] != 0 && visit[j] == 0){
visit[j] = 1;
cout << G.vexs[j] << " ";
Q.push(j);
}
}
}
}
}
5. Test case
#include<iostream>
using namespace std;
#include<queue>
#include<stdbool.h>
// Creation of adjacency matrix
typedef char vextype;// Vertex type customization
typedef int edgetype;// Custom weights on the edge
#define MAXVEX 100// Maximum number of vertices
#define MAXS 66666// Represents infinity
typedef struct
{
vextype vexs[MAXVEX];// Vertex table
edgetype arc[MAXVEX][MAXVEX];// Adjacency matrix
int numNodes;// Current number of vertices
int numEdges;// Current number of sides
}MGraph;
//1. The adjacency matrix representation of undirected network graph is established by reference
void CreatGraph(MGraph& G)
{
cout << " Please enter the number of vertices and edges :";
cin >> G.numNodes >> G.numEdges;
cout << " Please enter all vertex information :" << endl;
for (int i = 0; i < G.numNodes; i++)
cin >> G.vexs[i];
for (int i = 0; i < G.numNodes; i++)
for (int j = 0; j < G.numNodes; j++)
G.arc[i][j] = 0;
cout << " Please enter the edges composed of vertices and their weights :" << endl;
for (int i = 0; i < G.numEdges; i++)
{
int w, m, n;
cin >> m >> n >> w;
G.arc[m][n] = w;
G.arc[n][m] = G.arc[m][n];
}
}
//2. The pointer establishes the adjacency matrix representation of undirected network graph
/*void CreatGraph(MGraph* G) { cout << " Please enter the number of vertices and edges :"; cin >> G->numNodes >> G->numEdges; cout << " Please enter all vertex information :" << endl; for (int i = 0; i < G->numNodes; i++) cin>>G->vexs[i]; for (int i = 0; i < G->numNodes; i++) for (int j = 0; j < G->numNodes; j++) G->arc[i][j] = 0; cout << " Please enter the edges composed of vertices and their weights :" << endl; for (int i = 0; i < G->numEdges; i++) { int w, m, n; cin >> m >> n >> w; G->arc[m][n] = w; G->arc[n][m] = G->arc[m][n]; } }*/
//3. Depth first recursive algorithm of adjacency matrix
#define MAXVEX 100
int visit[MAXVEX] = {
0 };
void DFS(MGraph G, int i)
{
cout << G.vexs[i] << " ";
visit[i] = 1;
for (int j = 0; j < G.numNodes; j++)
{
if (!visit[j] && G.arc[i][j] != 0)
{
DFS(G, j);
}
}
}
void DFST(MGraph G)
{
for (int i = 0; i < G.numNodes; i++)
visit[i] = 0;
for (int i = 1; i < G.numNodes; i++)
{
if(!visit[i])
DFS(G, i);
}
}
// Print adjacency matrix
void PrintGraph(MGraph G)
{
int len = G.numNodes;
for (int i = 0; i < len; i++)
{
for (int j = 0; j < len; j++)
{
cout << G.arc[i][j] << " ";
}
cout << endl;
}
}
// Breadth first traversal algorithm of adjacency matrix
void BFS(MGraph G)
{
queue<vextype> Q;
for (int i = 0; i < G.numNodes; i++)
visit[i] = 0;
for (int i = 0; i < G.numNodes; i++)
{
if (!visit[i])
{
visit[i] = 1;
cout << G.vexs[i] << " ";
Q.push(i);
while (!Q.empty()){
Q.pop();
for (int j = 0; j < G.numNodes; j++)
if (G.arc[i][j] != 0 && visit[j] == 0)
{
visit[j] = 1;
cout << G.vexs[j] << " ";
Q.push(j);
}
}
}
}
}
int main()
{
MGraph G;
CreatGraph(G);
cout << " Print adjacency matrix " << endl;
PrintGraph(G);
cout << " The depth first traversal result of the adjacency matrix is :" << endl;
DFST(G);
cout << "\n The breadth first traversal result of the adjacency matrix is :" << endl;
BFS(G);
}
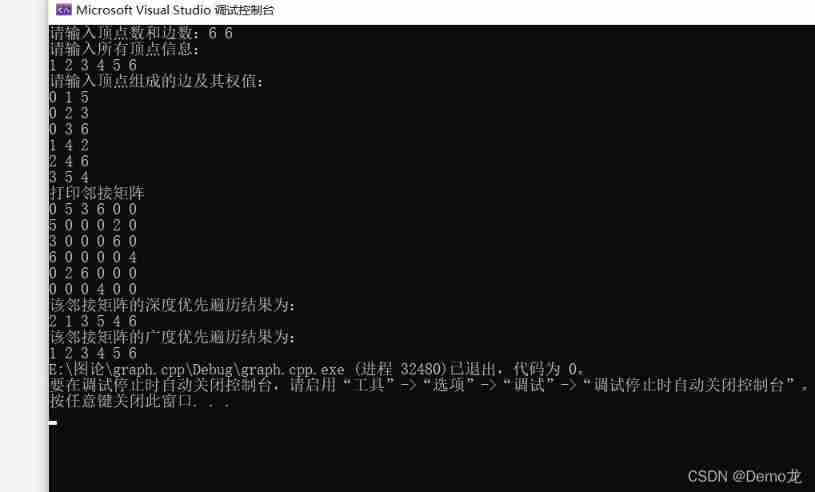
test result 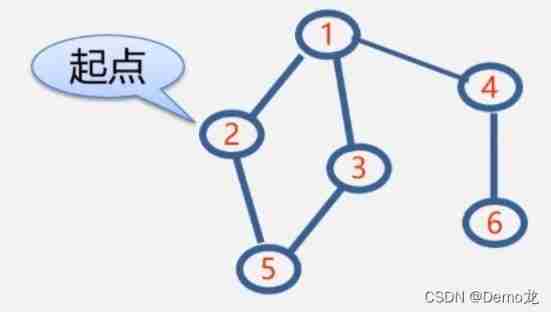
边栏推荐
- String comparison in batch file - string comparison in batch file
- Advanced learning of MySQL -- basics -- multi table query -- subquery
- 代码克隆的优缺点
- 【JokerのZYNQ7020】AXI_ EMC。
- 建立自己的网站(17)
- Learn to use code to generate beautiful interface documents!!!
- Use mujoco to simulate Cassie robot
- 在jupyter中实现实时协同是一种什么体验
- Chapter II proxy and cookies of urllib Library
- ActiveReportsJS 3.1中文版|||ActiveReportsJS 3.1英文版
猜你喜欢
How to judge whether an element in an array contains all attribute values of an object
Lombok 同时使⽤ @Data 和 @Builder 的坑,你中招没?
![[software reverse automation] complete collection of reverse tools](/img/72/d3e46a820796a48b458cd2d0a18f8f.png)
[software reverse automation] complete collection of reverse tools
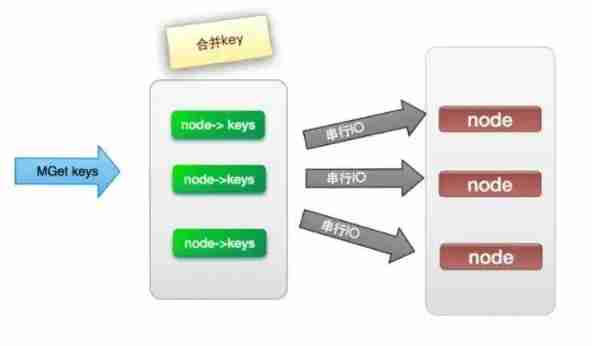
Deep understanding of distributed cache design
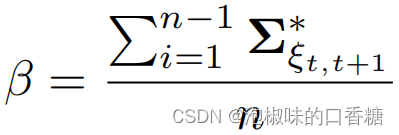
Attention SLAM:一種從人類注意中學習的視覺單目SLAM
做微服务研发工程师的一年来的总结
Dell Notebook Periodic Flash Screen Fault
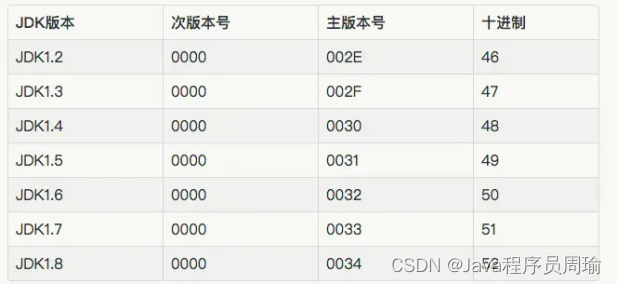
.class文件的字节码结构

迈动互联中标北京人寿保险,助推客户提升品牌价值

Mujoco second order simple pendulum modeling and control
随机推荐
新手如何入门学习PostgreSQL?
Cross-entrpy Method
Part IV: STM32 interrupt control programming
Stm32f407 ------- SPI communication
Learning notes 5: ram and ROM
paddlehub应用出现paddle包报错的问题
【软件逆向-求解flag】内存获取、逆变换操作、线性变换、约束求解
英雄联盟|王者|穿越火线 bgm AI配乐大赛分享
迈动互联中标北京人寿保险,助推客户提升品牌价值
[software reverse automation] complete collection of reverse tools
城联优品入股浩柏国际进军国际资本市场,已完成第一步
Leetcode(547)——省份数量
JS+SVG爱心扩散动画js特效
筑梦数字时代,城链科技战略峰会西安站顺利落幕
第七篇,STM32串口通信编程
ZABBIX 5.0: automatically monitor Alibaba cloud RDS through LLD
Advantages and disadvantages of code cloning
Zynq transplant ucosiii
【批处理DOS-CMD命令-汇总和小结】-查看或修改文件属性(ATTRIB),查看、修改文件关联类型(assoc、ftype)
stm32F407-------DAC数模转换