当前位置:网站首页>1.线性回归
1.线性回归
2022-07-07 23:11:00 【booze-J】
代码运行平台为jupyter-notebook,文章中的代码块,也是按照jupyter-notebook中的划分顺序进行书写的,运行文章代码,直接分单元粘入到jupyter-notebook即可。
1.导入第三方库
import keras
import numpy as np
import matplotlib.pyplot as plt
# Sequential 按顺序构成的模型
from keras.models import Sequential
# Dense 全连接层
from keras.layers import Dense
2.随机生成数据集
# 使用numpy生成100个随机点
x_data = np.random.rand(100)
# 噪音的形状和x_data的形状是一样的
noise = np.random.normal(0,0.01,x_data.shape)
# 设置w=0.1 b=0.2
y_data = x_data*0.1+0.2+noise
# y_data_no_noisy = x_data*0.1+0.2
# 显示随机点
plt.scatter(x_data,y_data)
# plt.scatter(x_data,y_data_no_noisy)
运行效果:
这是添加噪声的情况下y_data = x_data*0.1+0.2+noise: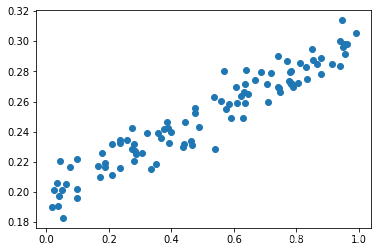
不添加噪声的情况下y_data_no_noisy = x_data*0.1+0.2(w=0.1,b=0.2):
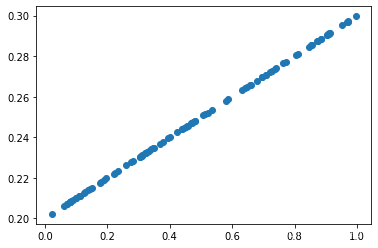
线性回归就是要根据添加噪声的散点图,拟合出一条与不添加噪声的散点图近似的直线。
3.线性回归
# 构建一个顺序模型
model = Sequential()
# 在模型中添加一个全连接层 在jupyter-notebook中,按shift+tab可以显示参数
model.add(Dense(units=1,input_dim=1))
# sgd:Stochastic gradient descent , 随机梯度下降法
# mse:Mean Squared Error , 均方误差
model.compile(optimizer='sgd',loss='mse')
# 训练3001个批次
for step in range(3001):
# 每次训练一个批次 的损失
cost = model.train_on_batch(x_data,y_data)
# 每500个batch打印一次cost
if step%500==0:
print("cost:",cost)
# 打印权值和批次值
W,b = model.layers[0].get_weights()
print("W:",W)
print("b:",b)
# x_data输入网络中得到预测值
y_pred = model.predict(x_data)
# 显示随机点
plt.scatter(x_data,y_data)
# 显示预测结果
plt.plot(x_data,y_pred,"r-",lw=3)
plt.show()
运行效果: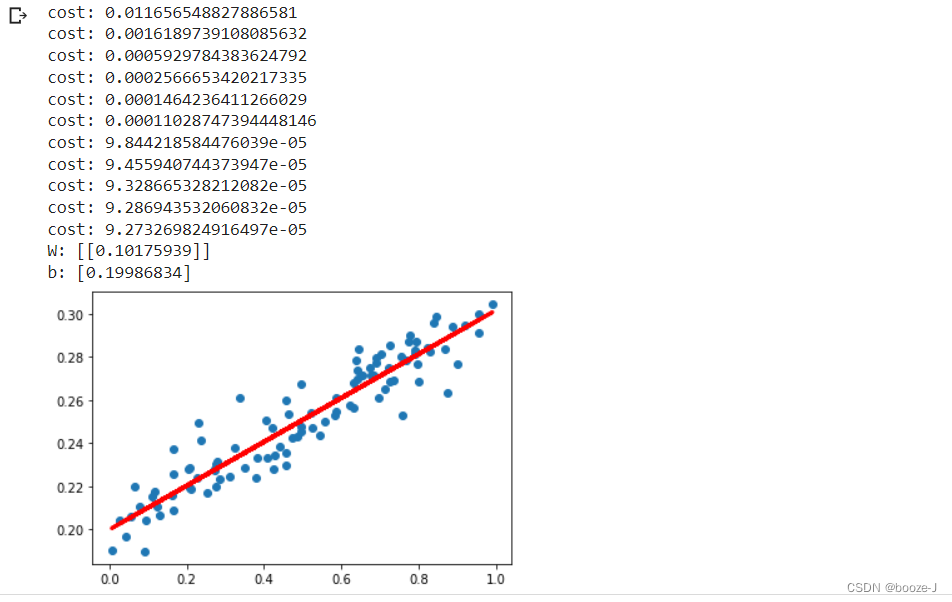
可以看到预测出来的w和b都十分接近我们设置的w和b。
注意
- 在jupyter-notebook中,按shift+tab可以显示参数
- train_on_batch的使用
- compile的使用
边栏推荐
- Basic principle and usage of dynamic library, -fpic option context
- Hotel
- Deep dive kotlin synergy (XXII): flow treatment
- What does interface testing test?
- Fofa attack and defense challenge record
- Vscode software
- NVIDIA Jetson test installation yolox process record
- Implementation of adjacency table of SQLite database storage directory structure 2-construction of directory tree
- Redis, do you understand the list
- 【愚公系列】2022年7月 Go教学课程 006-自动推导类型和输入输出
猜你喜欢
赞!idea 如何单窗口打开多个项目?
ThinkPHP kernel work order system source code commercial open source version multi user + multi customer service + SMS + email notification

fabulous! How does idea open multiple projects in a single window?
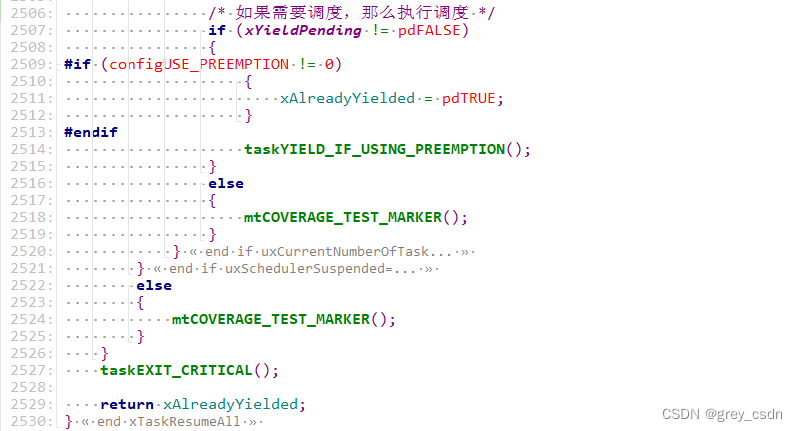
1293_FreeRTOS中xTaskResumeAll()接口的实现分析
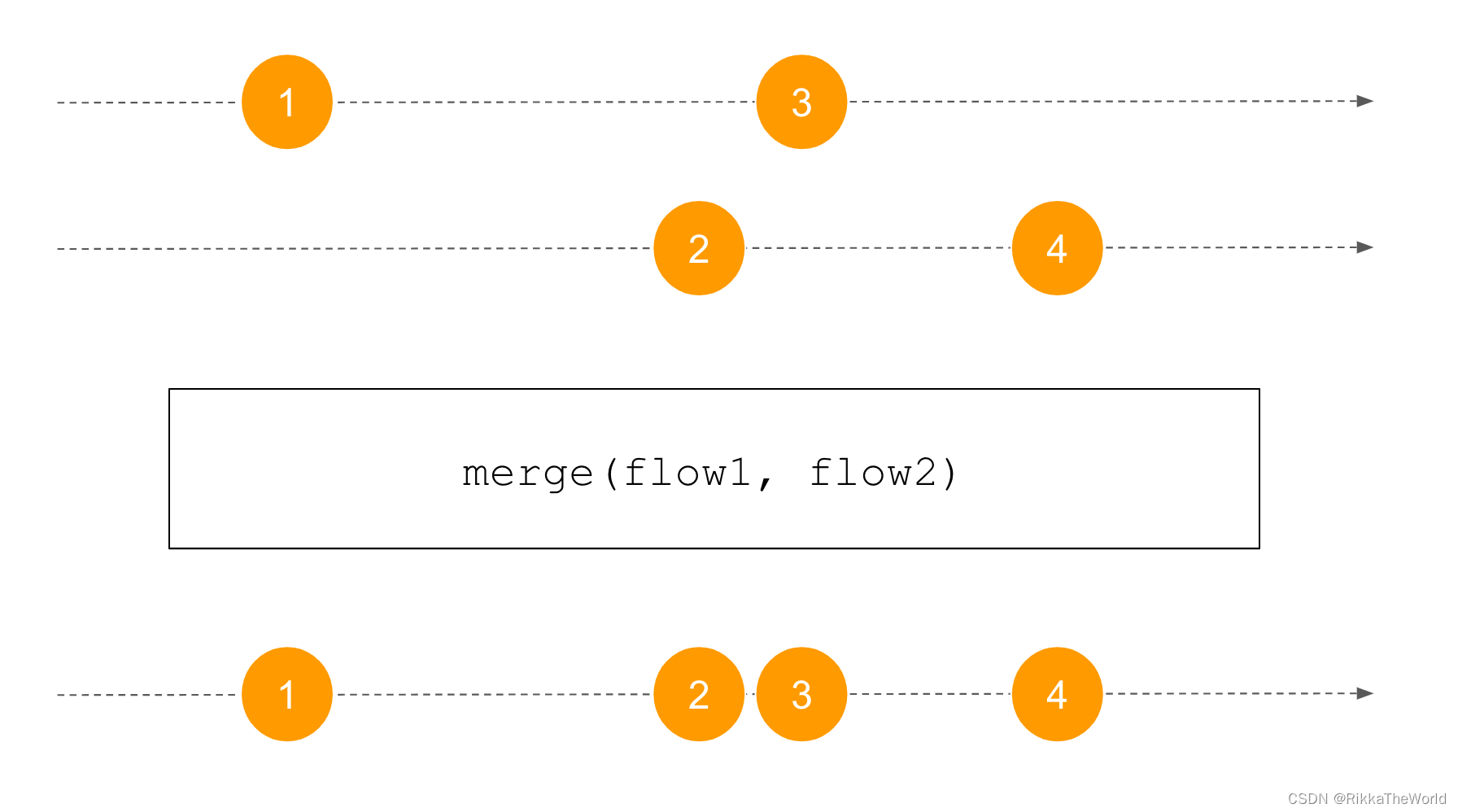
深潜Kotlin协程(二十二):Flow的处理
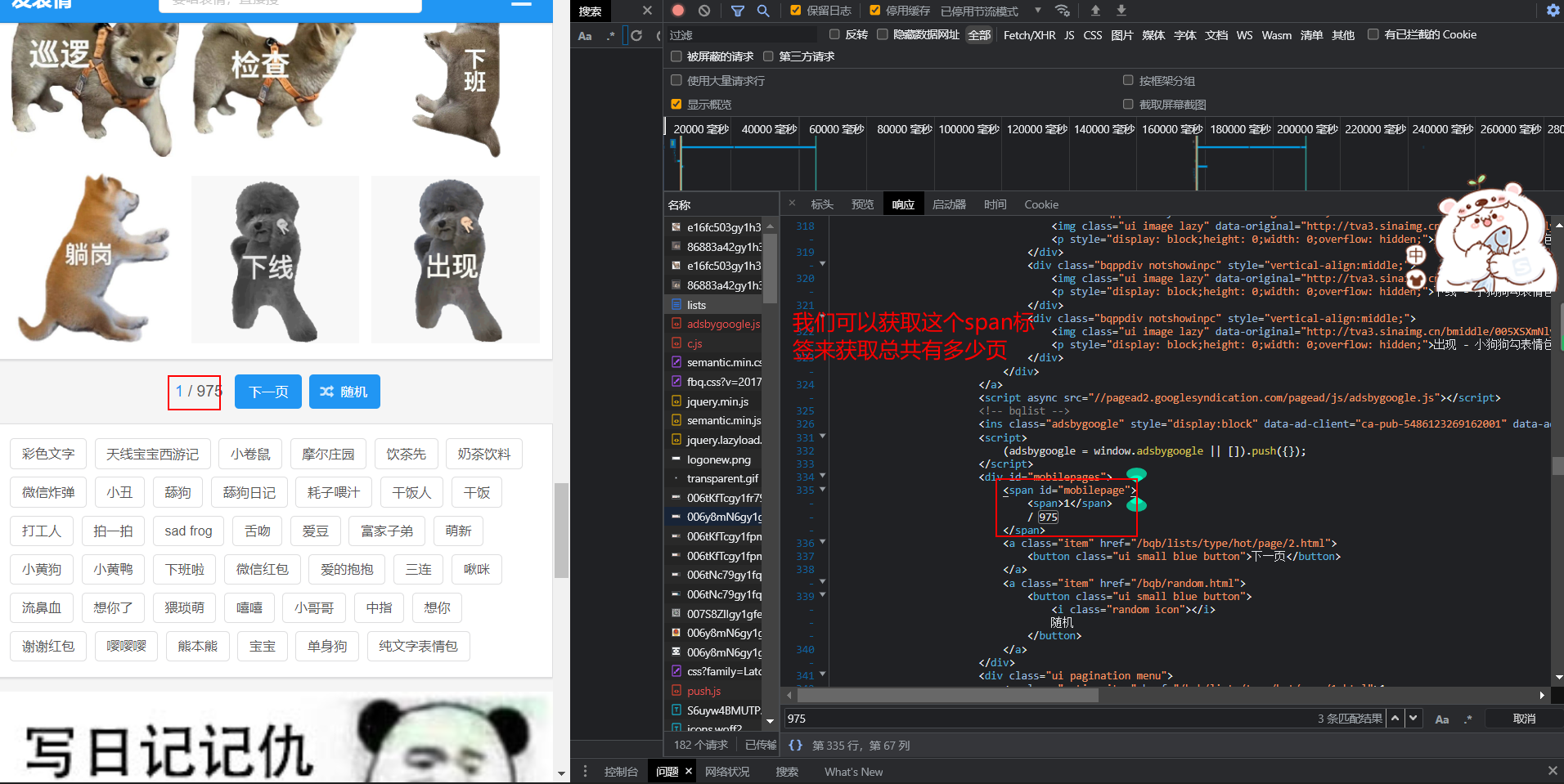
Reptile practice (VIII): reptile expression pack
Qt不同类之间建立信号槽,并传递参数
What does interface testing test?

《因果性Causality》教程,哥本哈根大学Jonas Peters讲授
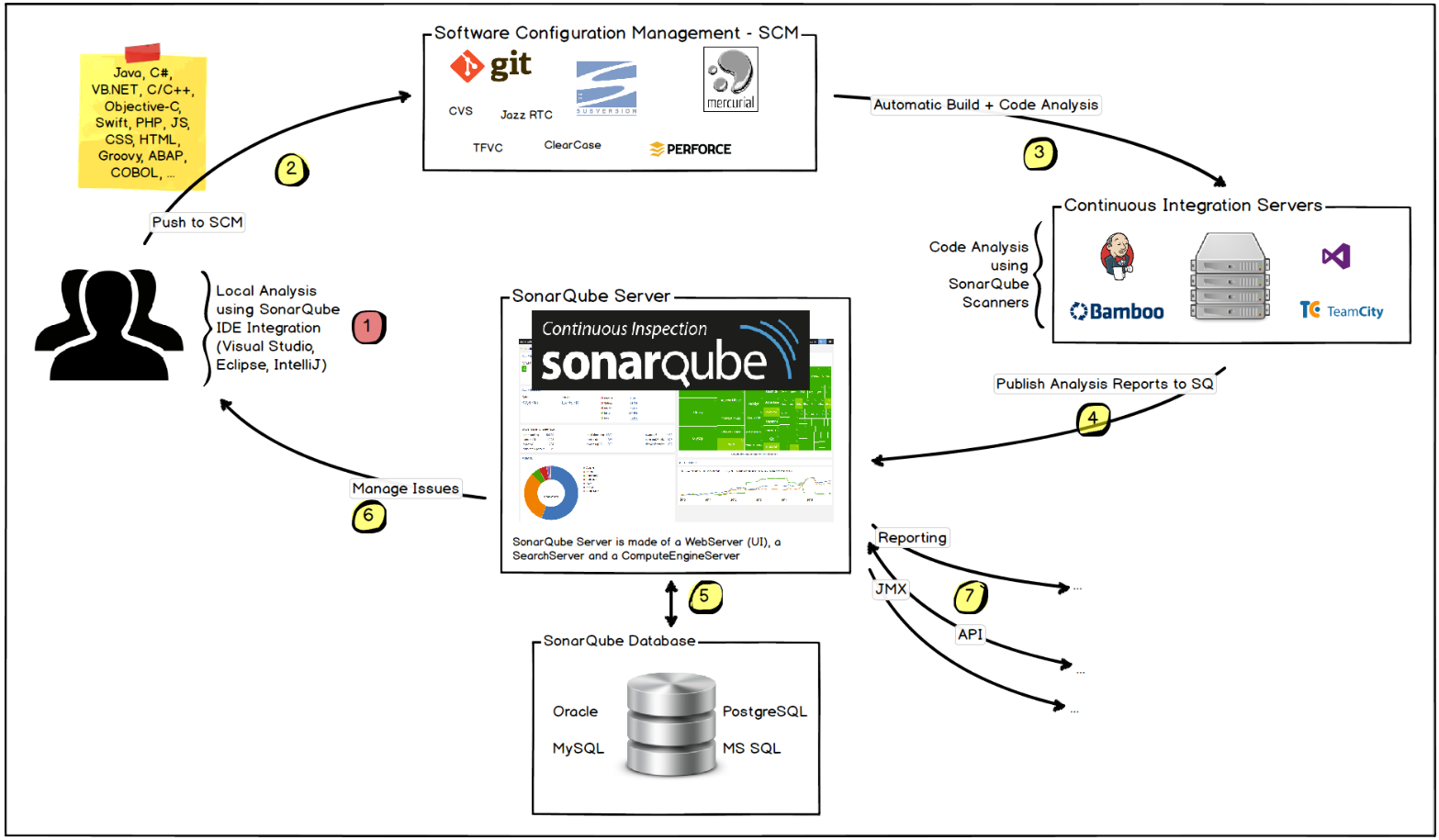
Play sonar
随机推荐
9. Introduction to convolutional neural network
Password recovery vulnerability of foreign public testing
What does interface testing test?
What is load balancing? How does DNS achieve load balancing?
Cause analysis and solution of too laggy page of [test interview questions]
2022-07-07: the original array is a monotonic array with numbers greater than 0 and less than or equal to K. there may be equal numbers in it, and the overall trend is increasing. However, the number
tourist的NTT模板
Reentrantlock fair lock source code Chapter 0
第四期SFO销毁,Starfish OS如何对SFO价值赋能?
Su embedded training - Day3
After going to ByteDance, I learned that there are so many test engineers with an annual salary of 40W?
Cancel the down arrow of the default style of select and set the default word of select
基于微信小程序开发的我最在行的小游戏
接口测试要测试什么?
1293_FreeRTOS中xTaskResumeAll()接口的实现分析
Reptile practice (VIII): reptile expression pack
letcode43:字符串相乘
[Yugong series] go teaching course 006 in July 2022 - automatic derivation of types and input and output
手写一个模拟的ReentrantLock
Summary of weidongshan phase II course content