4.交叉熵

交叉熵（cross-entropy）

1.二次代价函数（quadratic cost）

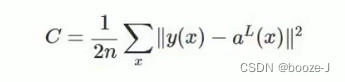
其中，c表示代价函数，x表示样本，y表示实际值，a表示输出值，n表示样本的总数。为简单起见，使用一个样本为例进行说明，此时二次代价函数为：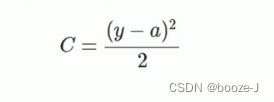

假如我们使用梯度下降法（Gradient descent）来调整权值参数的大小，权值w和偏置b的梯度推导如下：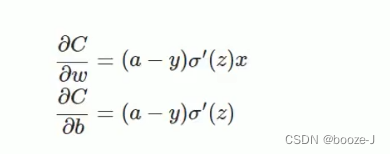

其中，z表示神经元的输入，$\alpha$表示激活函数。w和b的梯度跟激活函数的梯度成正比，激活函数的梯度越大，w和b的大小调整得越快，训练收敛得就越快。假设我们的激活函数是sigmoid函数：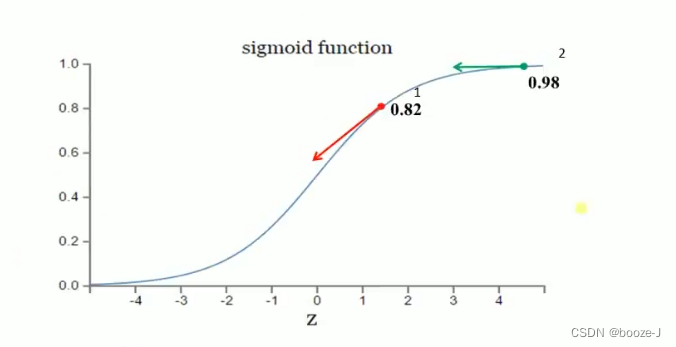

假设我们目标是收敛到1.0。1点为0.82离目标比较远，梯度比较大，权值调整比较大。2点为0.98离目标比较近，梯度比较小，权值调整比较小。调整方案合理。
假如我们目标是收敛到0.1点为0.82目标比较近，梯度比较大，权值调整比较大。2点为0.98离目标比较远，梯度比较小，权值调整比较小。调整方案不合理。

2.交叉熵代价函数（cross-entropy）

换一个思路，我们不改变激活函数，而是改变代价函数，改用交叉熵代价函数：

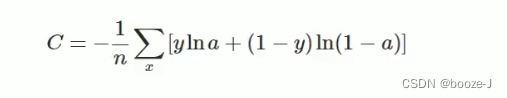
其中，C表示代价函数，x表示样本，y表示实际值，a表示输出值，n表示样本的总数。

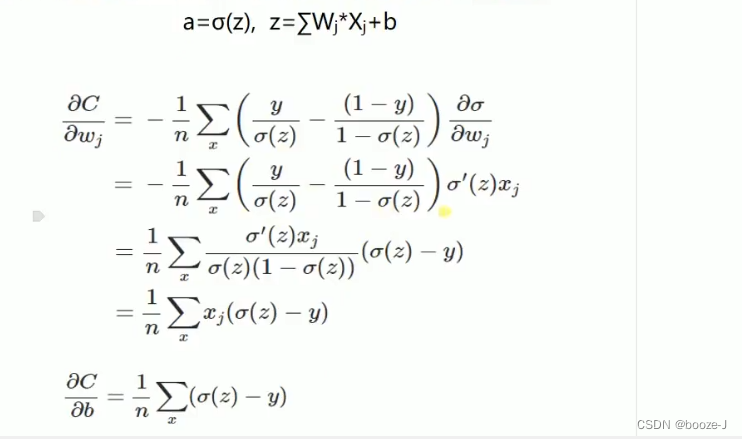
如果输出神经元是线性的，那么二次代价函数就是一种合适的选择。如果输出神经元是S型函数，那么比较适合用交叉熵代价函数。

3.对数释然代价函数（log-likelihood cost）

对数释然函数常用来作为softmax回归的代价函数，然后输出层神经元是sigmoid函数，可以采用交叉熵代价函数。而深度学习中更普遍的做法是将softmax作为最后一层，此时常用的代价函数是对数释然代价函数。
对数似然代价函数与softmax的组合和交叉熵与sigmoid函数的组合非常相似。对数释然代价函数在二分类时可以化简为交叉滴代价函数的形式。
在tensorflow中用：tf.nn.sigmoid_cross_entropy_with_logits()来表示跟sigmoid搭配使用的交叉嫡。
tf.nn.softmax_cross_entropy with_logits()来表示跟softmax搭配使用的交叉嫡。

简单使用

我们应用在3.MNIST数据集分类中的代码中，只需要修改简单的一句话。
将3.训练模型中的

# 定义优化器，loss_function,训练过程中计算准确率
model.compile(
    optimizer=sgd,
    loss="mse",
    metrics=['accuracy']
)

修改为

# 定义优化器，loss_function,训练过程中计算准确率
model.compile(
    optimizer=sgd,
    loss="categorical_crossentropy",
    metrics=['accuracy']
)

再运行整体代码：

对比3.MNIST数据集分类的运行结果，可以发现分类的模型使用交叉熵作为损失函数可以使得模型收敛更快，效果更佳。

完整代码

代码运行平台为jupyter-notebook，文章中的代码块，也是按照jupyter-notebook中的划分顺序进行书写的，运行文章代码，直接分单元粘入到jupyter-notebook即可。
1.导入第三方库

import numpy as np
from keras.datasets import mnist
from keras.utils import np_utils
from keras.models import Sequential
from keras.layers import Dense
from tensorflow.keras.optimizers import SGD

2.加载数据及数据预处理

# 载入数据
(x_train,y_train),(x_test,y_test) = mnist.load_data()
# (60000, 28, 28)
print("x_shape:\n",x_train.shape)
# (60000,) 还未进行one-hot编码 需要后面自己操作
print("y_shape:\n",y_train.shape)
# (60000, 28, 28) -> (60000,784) reshape()中参数填入-1的话可以自动计算出参数结果 除以255.0是为了归一化
x_train = x_train.reshape(x_train.shape[0],-1)/255.0
x_test = x_test.reshape(x_test.shape[0],-1)/255.0
# 换one hot格式
y_train = np_utils.to_categorical(y_train,num_classes=10)
y_test = np_utils.to_categorical(y_test,num_classes=10)

3.训练模型

# 创建模型 输入784个神经元，输出10个神经元
model = Sequential([
        # 定义输出是10 输入是784,设置偏置为1,添加softmax激活函数
        Dense(units=10,input_dim=784,bias_initializer='one',activation="softmax"),
])
# 定义优化器
sgd = SGD(lr=0.2)

# 定义优化器，loss_function,训练过程中计算准确率
model.compile(
    optimizer=sgd,
    loss="categorical_crossentropy",
    metrics=['accuracy']
)
# 训练模型
model.fit(x_train,y_train,batch_size=32,epochs=10)

# 评估模型
loss,accuracy = model.evaluate(x_test,y_test)

print("\ntest loss",loss)
print("accuracy:",accuracy)