Codeforces Round ＃804 (Div. 2)（A~D）

A. The Third Three Number Problem

Give a number n, Find three numbers a,b,c, Make these three numbers exclusive or to each other to get the sum of the three numbers equal n.

Ideas ： In fact, my idea is to see the first example to explain ,,

  Then I thought that two numbers could be the same , In this way, the sum of three numbers can be transformed into the sum of two numbers , And for even numbers , Direct use n/2 and 0 Exclusive or ; For odd numbers , In the example 1 dissatisfaction , Then I guess that odd numbers cannot meet the condition , Facts have proved that this can be proved ： Suppose the last bit of binary has k individual 1 and 3-k individual 0, that n The parity of the last bit of binary and k*(3-k) identical , that n The last bit of the binary should always be 0.

AC Code：

#include <bits/stdc++.h>

#define INF 0x3f3f3f3f
typedef long long ll;
const int mod=1e9+7;
const int N=55;
int t,n;

int main(){
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    std::cin>>t;
    while(t--){
    	std::cin>>n;
    	if(n&1){
    		std::cout<<-1<<'\n';
    		continue;
    	}
    	std::cout<<n/2<<' '<<n/2<<' '<<0<<'\n';
    }
    return 0;
}

B. Almost Ternary Matrix

Give two even numbers , Construct a 01 matrix , The number of squares around each square that is different from it is 2.

Ideas ： Try drawing it yourself , We will find that we can find one 4*4 Element matrix of , According to this unit matrix, you can output circularly , The identity matrix is as follows ：

 

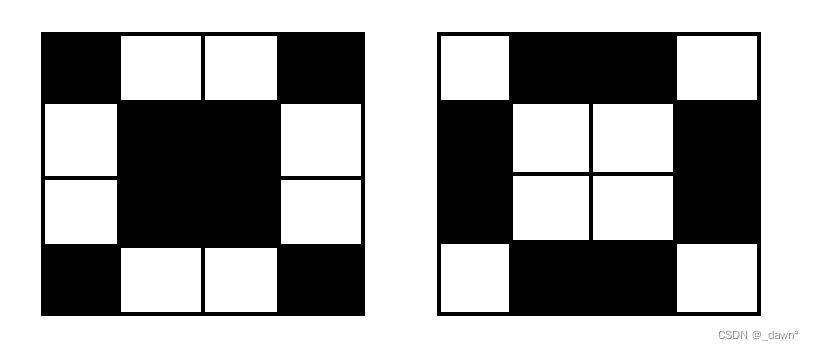
Of course ,01 interchangeable , So the code is very simple . 

 AC Code：

#include <bits/stdc++.h>

#define INF 0x3f3f3f3f
typedef long long ll;
const int mod=1e9+7;
const int N=55;
int t,n,m;
int ans[4][4]={1,0,0,1,0,1,1,0,0,1,1,0,1,0,0,1};

int main(){
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    std::cin>>t;
    while(t--){
    	std::cin>>n>>m;
    	for(int i=0;i<n;i++){
    		for(int j=0;j<m;j++){
    			std::cout<<ans[i%4][j%4]<<" \n"[j==m-1];
    		}
    	}
    }
    return 0;
}

os： At first, I thought about how to write code for a long time hhhhh

C. The Third Problem

Give a permutation, But from 0~n-1, Ask how many ways to rearrange these numbers , Make the reordered array for each interval MEX The values are equal .

Ideas ： See this question , It's probably a problem similar to permutation and combination . According to our observation, we can find that , For each number , As long as this number goes forward and backward, there are elements smaller than this number , Then this number can move within this range , Examples 4：

1 3 7 2 5 0 6 4    

Than 2 The small ones are just 0 and 1, that 2 You can do it on the 2 Move to the fifth position ;3 It can only move within this range , Because than 3 The smallest number can only reach 0 and 1 The location of ; And for the number around the number smaller than yourself , Their position is immovable , such as 4, Smaller than it 0,1,2,3 It's all in front , It's easy to understand if its position changes , There must be an interval MEX The value has changed. . According to this property , We can sort by number , Enumerate from small to large , Constantly update the maximum range of numbers smaller than the current number , There are several ways to choose the position for calculating each number , Multiply by . Of course ,0 and 1 As the initial interval range ,0 and 1 The position of must not move .

AC Code：

#include <bits/stdc++.h>

#define INF 0x3f3f3f3f
typedef long long ll;
const int mod=1e9+7;
const int N=1e5+5;
int t,n;
int a[N];

struct node{
	int id,num;
	bool operator<(const node &a) const{
		return num<a.num;
	}
} e[N];

int main(){
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    std::cin>>t;
    while(t--){
    	std::cin>>n;
    	for(int i=1;i<=n;i++){
    		std::cin>>a[i];
    		e[i].id=i;
    		e[i].num=a[i];
    	}
    	std::sort(e+1,e+1+n);
    	int r=-1,l=1e9;
    	ll ans=1;
    	for(int i=1;i<=n;i++){
    		r=std::max(r,e[i].id);
    		l=std::min(l,e[i].id);
    		if(i>2&&e[i].id>l&&e[i].id<r){
    			ans*=(r-l-1-i+3);
    			ans%=mod;
    		}
    	}
    	std::cout<<ans<<'\n';
    }
    return 0;
}

os： Finish the first two questions in more than 20 minutes , I kept thinking C, In the last five minutes hhhh

D. Almost Triple Deletions

Give an array , If two adjacent numbers are different , Then you can delete these two numbers . After the final operation is completed, the remaining numbers in the array are equal , Ask how many numbers you can keep at most .

Ideas ： Study Big guy's idea , That's too much

We can think that the final result of the operation is to delete some continuous intervals , And for an interval [l,r] Come on , If and only if the following conditions are met , You can delete ： The interval length is even ; The maximum number of elements that appear most frequently in the interval is (r-l+1)/2.

The necessity must , Proof of sufficiency ：

For the most frequent number , There must be a way , Delete one and another number , Then the number of occurrences remaining t<=(r-l+1)/2-1; If you delete , This number is still the most frequent , Then it still meets the initial conditions , You can still delete one number and another number ; If it doesn't appear the most after deletion , Then there must be another number that satisfies the initial condition of the largest number of occurrences , You can delete one of the numbers and another number , This is the mutual transformation between elements in this interval , At last, when the equilibrium is reached, the occurrence times of the two elements are equal , All equal to l/2, This must be deleted , Make the interval as long as 0, Certificate completion .

So we can first deal with sub intervals that can be deleted ,cel[l][r]=1, We define DP Array f[i] It means from the first to i Number , Delete some numbers until all numbers are equal to a[i] after , The maximum number of remaining ,f[i] To f[j] The transformation equation of can be expressed as deleting interval [j,i], bring f[i]=f[j]+1.

The final answer is not necessarily f[n], Because the last remaining numbers are not necessarily equal to a[n], So you need to scan it once to get the maximum value .

Data range n<=5000,O(n^2) Yes .

AC Code：

#include <bits/stdc++.h>

#define INF 0x3f3f3f3f
typedef long long ll;
const int mod=1e9+7;
const int N=5e3+5;
int t,n;
int a[N];

int main(){
	std::ios::sync_with_stdio(false);
	std::cin.tie(0);
	std::cout.tie(0);
	std::cin>>t;
	while(t--){
		std::cin>>n;
		for(int i=1;i<=n;i++){
			std::cin>>a[i];
		}
		int cel[n+1][n+1]={0};
		for(int l=1;l<=n;l++){
			int cnt[n+1]={0},max=0;
			for(int r=l;r<=n;r++){
				cnt[a[r]]++;
				max=std::max(max,cnt[a[r]]);
				if((r-l+1)%2==0&&max*2<=r-l+1)
					cel[l][r]=1;
			}
		}
		int f[n+1]={0};
		int ans=0;
		for(int i=1;i<n;i++){
			if(cel[1][i])
				f[i+1]=1;
		}
		f[1]=1;
		for(int i=1;i<=n;i++){
			for(int j=1;j<i;j++){
				if((j+1>i-1||cel[j+1][i-1]==1)&&a[j]==a[i]&&f[j]>0)
					f[i]=std::max(f[i],f[j]+1);
			}
			if(i==n||cel[i+1][n]) ans=std::max(ans,f[i]);
		}
		std::cout<<ans<<'\n';
	}
	return 0;
}

os： blame , This question card memset

Hey, hey, hey , Qingla qingla ！

  If there is any mistake, please advise , thank you ！