当前位置:网站首页>Overview of three core areas of Mathematics: geometry
Overview of three core areas of Mathematics: geometry
2022-07-06 06:03:00 【Zhan Miao】
Mathematics has developed to the present , It has become owned in the scientific world 100 A large number of major sub disciplines “ republic ”. Generally speaking, mathematics has three core areas :
The part of mathematics that studies numbers belongs to the category of algebra ;
Study the part of form , It belongs to the fan Chou of geometry ;
The part that communicates form and number and involves limit operation , It belongs to the scope of analysis .
These three kinds of mathematics constitute the ontology and core of the whole mathematics . Around this core , Because mathematics passes the two concepts of number and shape , Permeate with other sciences , And there are many marginal and interdisciplinary disciplines . This paper briefly introduces the historical development of more than ten main branches of mathematics in the three core fields .
1. Elementary Geometry
In Greek ,“ geometry ” By “ The earth ” And “ measurement ” It came from the merger , It originally has the meaning of measuring land , Paraphrase is “ Geodesy ”.“ geometry ” The term , It was translated by mathematicians in Ming Dynasty according to pronunciation , Still in use today .
Now elementary geometry mainly refers to Euclidean geometry , It is about graphics ( spot 、 Line 、 Noodles 、 horn 、 Circle, etc. ) Science of unchanging nature under motion . for example , The distance between two points in Euclidean geometry , The intersection angle of two straight lines , Radius is r The area of a circle of is some motion invariants .
Elementary geometry as a course , Arranged after elementary algebra ; But in history , The development of geometry once took precedence over algebra , It is mainly considered to be the contribution of the ancient Greeks .
Geometry discards all other properties of matter , Only the spatial form and relationship are reserved as the objects of my own research , So it is abstract . This abstraction determines the thinking method of geometry , It is necessary to use the method of reasoning , Derive some new conclusions from some conclusions . The theorem is proved by deduction , The representative work of this argumentation geometry , It is Euclid in the third century BC 《 Original 》, It starts from definition and axiom , Deduce various geometric theorems .
Now middle school 《 Plane triangle 》 The theory of trigonometric function in is 15 Developed and perfected in the 21st century , But some of its most basic concepts , However, it has been formed as early as the ancient study of right triangle . therefore , Trigonometry can be classified under the heading of elementary geometry .
Ancient Egypt 、 Babylon 、 China 、 Greece has studied the knowledge of spherical trigonometry . B.c. 2 century , Hippachas made a string watch , It can be said to be the founder of triangle . Later, Indians made sine tables ; Arab al · Batani calculated sinθ Value method to solve the equation , He is also with arbour · Wofa jointly derived the tangent 、 Cotangent 、 Secant 、 The concept of cosecant ; Ricius made a more accurate sine table , And connect trigonometric functions with arcs .
Because a right triangle is the simplest straight line , It also has very important practical value , Therefore, all ancient civilizations attach great importance to its research . In our country 《 Zhou Bi Suan Jing 》 The early years of the Zhou Dynasty were recorded at the beginning ( B.c. 1100 About years ago ) The dialogue between Duke Zhou and scholar Shang Gao , Among them “ Hook three strands, four strings and five ”, That is, the special form of Pythagorean theorem ; It also records Chen Zi after the Duke of Zhou , I used Pythagorean theorem and the proportional relationship of similar figures , Calculated the distance between the earth and the sun and the diameter of the sun , At the same time, there are dozens of illustrations for Pythagorean theorem . Beyond seas , Traditionally, Pythagorean theorem is called Pythagorean theorem , It is believed that the first proof of consistency comes from the Pythagorean School ( B.c. 6 century ), Although the Babylonians used to 1000 This theorem has been discovered for many years . Until now, people have at least provided the Pythagorean theorem 370 Kind of proof .
19 Since the 20th century , People are interested in elementary comprehensive geometry about triangles and circles , And conducted in-depth research . So far, this research field has not come to an end , Many data have been extended to tetrahedron and accompanying points 、 Line 、 Noodles 、 The ball .
2. Projective geometry
Projective geometry is a study of projecting points onto a line or plane , A geometry of the invariant properties of graphs . Points on the slide 、 Line , After the illumination projection of the slide projector , There are corresponding dots and lines in the pictures on the screen , After a finite number of perspectives, such a group of figures , Become another set of graphics , This is called projective correspondence in Mathematics . Projective geometry in aviation 、 Photography and surveying are widely used .
Projective geometry is where deshag and Pascal are 1639 Opened in . Deshag published — This very original pamphlet about circular dimensional curves , Start with Kepler's continuity principle , We have derived a lot about involution 、 Harmonic range 、 transmission 、 Polar axis 、 The pole and the basic principle of perspective , These topics are familiar to those who study projective geometry today . Years old 16 Pascal, 19, came up with some new 、 A profound theorem , And in 9 Years later, he wrote a manuscript with rich content .18 In the late 20th century , Mengri proposed a method to express three-dimensional objects by appropriate projection on two-dimensional plane , Therefore, the position of artillery positions can be quickly calculated from the data provided , Avoid lengthy 、 Troublesome arithmetic operation .
The truly independent study of projective geometry was initiated by penseller .1822 year , He published 《 On the projective properties of figures 》 One article , It will greatly promote the research in this field . Many of his concepts were further developed by Steiner .1847 year , Stout published 《 Positional geometry 》 A Book , Finally, projective geometry is liberated from the basis of measurement .
Later it turned out that , Adopt a projective definition with appropriate metrics , Be able to study metric geometry within the scope of projective geometry . Add an invariant conic to projective geometry on a plane , You can get the traditional non Euclidean geometry . stay 19 The late 19th century and 20 At the beginning of the century , Projective geometry has been treated with various postulates , And finite projective geometry has also been found . The fact proved that , Gradually add and change public facilities , You can transition from projective geometry to Euclidean geometry , During this period, I experienced many other important geometries .
3. Analytic geometry
Analytic geometry is coordinate geometry , It includes plane analytic geometry and solid analytic geometry . Analytic geometry passes through plane rectangular coordinate system and space rectangular coordinate system , Establish a one-to-one correspondence between points and real pairs , Thus, a one-to-one correspondence between the curve or surface and the equation is established , Therefore, we can study geometric problems with algebraic methods , Or use geometric methods to study algebraic problems .
In Elementary Mathematics , Geometry and algebra are two independent branches ; On the way , They are also basically irrelevant . Establishment of analytic geometry , Not only because of the introduction of variable research in the content, but also created variable Mathematics , Moreover, it also combines geometric methods with algebraic methods .
While dishag and Pascal developed projective geometry , Descartes and Fermat began to conceive the concept of modern analytic geometry . There is a fundamental difference between the two studies : The former is a branch of geometry , The latter is a method of geometry .
1637 year , Descartes published 《 methodology 》 And its three appendices , His contribution to analytic geometry , In the third appendix 《 geometry 》 in , He proposed several new curves generated by mechanical motion . stay 《 Introduction to plane and solid trajectories 》 in , Fermat analytically defines many new curves . For the most part , Descartes starts from the track , Then find its equation ; Fermat starts from the equation , Then study the trajectory . These are exactly two opposite aspects of the basic principles of analytic geometry ,“ Analytic geometry ” The name of is decided later .
This course reaches the familiar form in current textbooks , yes 100 Years later . Use coordinates like today 、 Abscissa 、 The terms of ordinate , It was Leibniz in 1692 Put forward in .1733 year , Years old 18 The year-old crallo published 《 Research on double curvature curve 》 A Book , This is the earliest work on analytic geometry of space .1748 year , Written by Euler 《 Summary of infinite analysis 》, It can be said to be the first course of analytic geometry in line with modern significance .1788 year , Lagrange began to study the theory of directed line segments .1844 year , Glassman put forward the concept of multidimensional space , And introduce the notation of vector . So multidimensional analytic geometry appeared .
The development of analytic geometry in modern times , It produces some branches of infinite dimensional analytic geometry and algebraic geometry . Ordinary analytic geometry is just a part of algebraic geometry , The development of algebraic geometry is closely related to abstract algebra .
4. Non Euclidean geometry
Non Euclidean geometry has three different meanings : The narrow sense , One finger Roche ( Robachevsky ) The geometric ; The generalized , It refers to everything and Euclidean ( Euclid ) Geometrically different geometries ; In the usual sense , Refers to Roche geometry and Riemann geometry .
Euclid's first 5 Public establishment ( Parallel public establishment ) It occupies a special position in the history of Mathematics , It's the same as before 4 Compared with the postulate , The nature is too complicated . It's in 《 Original 》 The first application of is to prove that 29 When there is a theorem , And it always seems to try to avoid using it . Therefore, people doubt the axiomatic status of the fifth postulate , And explore other axioms to prove it , To make it a theorem . For more than 3000 years , More than 2000 people have made such explorations and have records , Including many famous mathematicians , But they all failed .
Robachevsky in 1826 year , Bowyer in 1832 In, he published epoch-making research results , Created non Euclidean geometry . In this geometry , They assume that “ Pass a point that is not on a known straight line , At least two lines can be drawn parallel to the known line ”, To replace the fifth postulate , At the same time, other postulates of Euclidean geometry are preserved .
1854 year , Riemann introduced another kind of non Euclidean geometry . In this geometry , He assumes that “ Pass a point beyond a known straight line , There is no straight line parallel to the known straight line to lead ”, Used instead of 5 Public establishment , At the same time, other postulates of Euclidean geometry are preserved .1871 year , Klein put this 3 Kind of geometry : Robachevsky — Bowyer's 、 Euclidean and Riemannian are respectively named hyperbolic geometry 、 Parabolic geometry and elliptic geometry .
The discovery of non Euclidean geometry not only finally solves the problem of parallel postulates —— The parallel postulate is proved to be independent of other postulates of Euclidean geometry , And liberate geometry from its traditional model , The path of geometry that created many different systems was opened .
1854 year , Riemann published “ A lecture on assumptions as the basis of geometry ”. He pointed out that : Each of them is different ( Two infinitely close points ) The distance formula determines the properties of the resulting space and geometry .1872 year , Klein established a classification method of various geometric systems according to different transformation group invariants .
19 After the century , Another direction of the development of the concept of geometric space , It is a classification according to the differential geometric principles of the manifold studied , Every geometry corresponds to a system of theorems .1899 year , Hilbert published 《 Geometric basis 》 A Book , A complete system of geometric axioms is proposed , The rigorous foundation of Euclidean geometry is established , The compatibility of an axiom system is proved ( No contradiction )、 The universal principles of independence and completeness . According to his point of view , Different geometric spaces are sets of elements that are subordinate to the requirements of different geometric axioms . Euclidean geometry and non Euclidean geometry , In a large number of geometric systems , It's just an extremely special situation .
5. Topology
1736 year , Euler published a paper , Discuss the problem of the Seven Bridges in gunnysburg . He also proposed that spherical triangles divide graph vertices 、 edge 、 Euler formula of the relationship between faces , This can be said to be the beginning of topology .
Poincare in 1895~1904 Topology was established in , Topological properties are studied by algebraic combination . He extended Euler's formula to Euler — Poincare formula , The theories related to this are now called homology theory and homotopy theory . Later topology developed mainly according to Poincare's ideas .
Topology began as a branch of geometry , In the 20th century, it has been greatly promoted .1906 year , Frecher published his doctoral thesis , Take the function as a “ spot ” Look at , Describe the function convergence as the convergence of points , This connects Cantor's point set theory with the abstraction of analysis . He introduced the concept of distance into the set of functions , Form a distance space , Expand the theory of linear distance space . On this basis , Produces point set topology . In Hausdorf's 《 Outline of point set theory 》 In a Book , The complete idea of more general point set topology has emerged . After the Second World War , Introduce analysis into topology , Developed differential topology .
Now topology can be roughly defined as the mathematical study of continuity . The set of everything can form a topological space in a sense , The concepts and theories of topology have been basically completed and become one of the basic theories of Mathematics , Infiltrate into all branches , And it has been successfully applied to the research of electromagnetism and Physics .
边栏推荐
猜你喜欢
MPLS test report

【课程笔记】编译原理
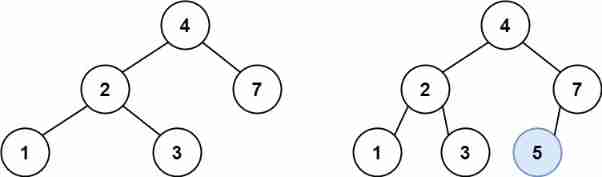
Leetcode 701 insertion operation in binary search tree -- recursive method and iterative method
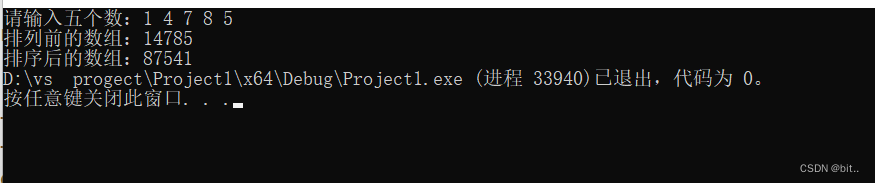
c语言——冒泡排序
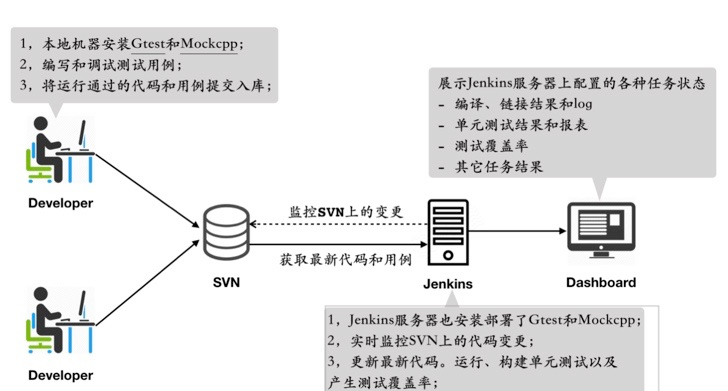
单元测试的意义
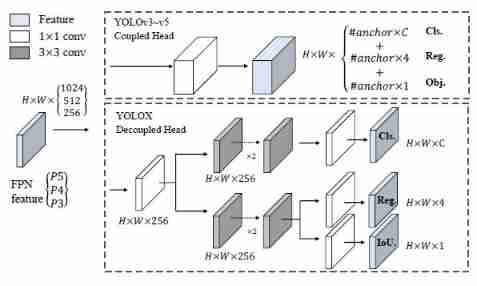
Construction of yolox based on paste framework

Report on market depth analysis and future trend prediction of China's arsenic trioxide industry from 2022 to 2028
Web service connector: Servlet
![[happy Spring Festival] if you feel happy, dance](/img/b5/faa4cb94ef5fb45b8bb98ecb69962f.jpg)
[happy Spring Festival] if you feel happy, dance
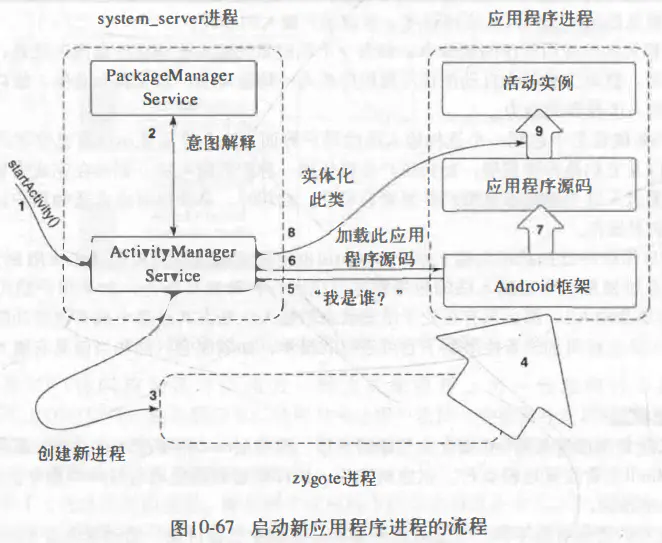
进程和线程
随机推荐
Embedded interview questions (I: process and thread)
Luogu p1460 [usaco2.1] healthy Holstein cows
Linux regularly backs up MySQL database
Baidu online AI competition - image processing challenge: the 8th program of handwriting erasure
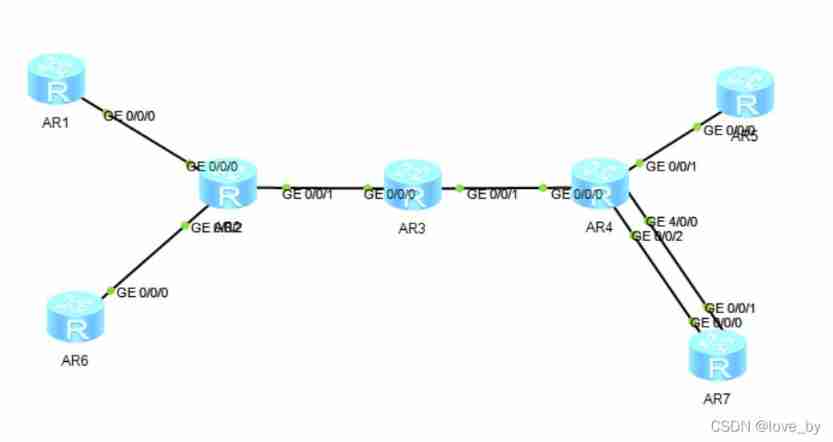
How Huawei routers configure static routes
P2802 go home
ContentType的作用
Dynamic programming -- knapsack problem
Eigen稀疏矩阵操作
数学三大核心领域概述:几何
假设检验学习笔记
IPv6 comprehensive experiment
[Baiwen smart home] first day of the course_ Learn Embedded and understand the development mode of bare metal and RTOS
Sqlmap tutorial (III) practical skills II
华为路由器如何配置静态路由
Cognitive introspection
Raised a kitten
isam2运行流程
Expose the serial fraudster Liu Qing in the currency circle, and default hundreds of millions of Cheng Laolai
异常检测方法总结