当前位置:网站首页>VINS-Mono: A Robust and Versatile Monocular Visual-Inertial State Estimator
VINS-Mono: A Robust and Versatile Monocular Visual-Inertial State Estimator
2022-07-06 05:58:00 【瞻邈】
港科大的VINS-Mono作为目前state of the art的开源VIO项目,是研究视觉与IMU紧耦合的必读算法,网上的论文解读与代码实现也非常丰富(感谢!)。为更好地进行学习,本人在几篇VINS论文解读与翻译的参考与改进下,完成了自己对全文的阅读与翻译,以后将逐步更新自己对算法的解读,欢迎大家一起讨论。
原文:VINS-Mono A Robust and Versatile Monocular Visual-Inertial State Estimator
VINS代码地址:https://github.com/HKUST-Aerial-Robotics/VINS-Mono
VINS-Mono:一种鲁棒且通用的单目视觉惯性状态估计器
摘要:由一个相机和一个低成本惯性测量单元(IMU)组成的单目视觉惯性系统(VINS),构成了用于度量六自由度状态估计的最小传感器套件。然而,由于缺乏直接距离测量,在IMU处理、估计器初始化、外部标定和非线性优化等方面提出了重大挑战。本文提出了VINS-Mono:一种具有鲁棒性和通用性的单目视觉惯性状态估计器。该方法从用于估计器初始化和故障恢复的鲁棒的程序开始。采用一种基于紧耦合、非线性优化的方法,通过融合预积分后的IMU测量值和特征观测值,获得高精度的视觉惯性里程计。结合紧耦合方法,回环检测模块能够以最小的计算代价实现重定位。此外,我们还进行四自由度位姿图优化,以加强全局一致性。我们验证了该系统在公共数据集和真实环境实验的性能,并与其他最先进的算法进行了比较。我们还在MAV平台上执行机载闭环自主飞行,并将算法移植到基于iOS的demo中。特别强调的是,本文提出的工作是一个可靠、完整和通用的系统,适用于需要高精度定位的不同应用。我们为PC和iOS移动设备开源了我们的实现方法。
关键词:单目视觉惯性系统,状态估计,传感器融合,SLAM
I. 引言
状态估计无疑是机器人导航、自主驾驶、虚拟现实(VR)和增强现实(AR)等广泛应用中最基本的模块。仅使用单目摄像机的方法由于其体积小、成本低和硬件设置简单而获得了社会的极大兴趣[1]-[5]。然而,单目视觉系统无法恢复度量尺度,因此限制了它们在实际机器人中的应用。近年来,我们看到了一种发展趋势,即用低成本惯性测量单元(IMU)辅助单目视觉系统。这种单目视觉-惯性系统(VINS)的主要优点是具有可观测的度量尺度,以及翻滚角(roll)和俯仰角(pitch)。这让需要有尺度的状态估计的导航任务成为可能。此外,对IMU测量值的积分可以显著提高运动跟踪性能,弥补光照变化、缺少纹理的区域或运动模糊的视觉轨迹损失的差距。事实上,单目VINS不仅广泛应用于移动机器人、无人机和移动设备上,还是满足充分自我感知和环境感知的最小传感器。
然而,所有这些优点都是有代价的。对于单目VINS,众所周知,需要加速度激励以测量尺度。这意味着单目VIN估计器不能从静止状态启动,而是从未知的移动状态发动。同时要认识到视觉惯性系统高度非线性的事实,在估计器初始化方面还有重大挑战。两个传感器的存在也使得摄像机-IMU的外部校准至关重要。最后,为了消除在可接受的处理窗口内的长期漂移,提出了一个完整的系统,包括视觉惯性里程计、回环检测、重定位和全局优化。
为了解决所有这些问题,我们提出了VINS-Mono,一个鲁棒且通用的单目视觉惯性状态估计器。我们的解决方案开始于即时估计初始化。这个初始化模块也用于故障恢复。我们的解决方案的核心是一个鲁棒的基于紧耦合的滑动窗非线性优化的单目视觉惯性里程计(VIO)。单目VIO模块不仅提供精确的局部姿态、速度和方位估计,而且还以在线方式执行摄像机IMU外部校准和IMU偏置校正。使用DBoW2[6]进行回环检测。重新定位是在对单目VIO进行特征级别融合的紧耦合设置中完成。这使得重新定位具有鲁棒性和精确性且有最小的计算代价。最后,几何验证的回环被添加到位姿图中,并且由于来自单目VIO的可观测的翻滚角和俯仰角,生成四自由度(DOF)位姿图以确保全局一致性。
VINS-Mono结合并改进了我们先前在单目视觉-惯性融合方面的工作[7]-[10]。它建立在我们紧耦合、基于优化的单目VIO的公式之上[7][8],并结合了[9]中引入的改进初始化过程。[10]中给出了移植到移动设备的第一次尝试。与我们以前的工作相比,VINS-Mono的进一步改进包括改进的含偏置校正的IMU预积分、紧耦合重定位、全局位姿图优化、广泛的实验评估以及鲁棒和通用的开源实现。
整个系统完整且易于使用。它已经被成功应用于小规模AR场景、中型无人机导航和大规模状态估计任务。与其他最先进的方法相比具有优异的性能。为此,我们总结了我们的贡献,如下所示:
1. 一个鲁棒的初始化过程,它能够从未知的初始状态引导系统。
2. 一个紧耦合、基于优化的单目视觉惯性里程计,具有相机-IMU外部校准和IMU偏置估计。
3. 在线回环检测与紧耦合重定位。
4. 四自由度全局位姿图优化。
5. 用于无人机导航、大规模定位和移动AR应用的实时性能演示。
6. 完全集成于ros的pc版本以及可在iphone 6或更高版本上运行的IOS版本的开源代码。
论文的其余部分如下:在第二节中,我们讨论了相关的文献。在第三节中,我们对完整的系统框架进行了概述。在第四节中,给出了视觉的预处理和IMU测量值的预积分步骤。在第五节中,我们讨论了估计器的初始化过程。在第六节中提出了一种紧耦合、自标定、非线性优化的单目VIO。第七节和第八节分别给出了紧耦合重定位和全局位姿图优化。实施细节和实验结果见第九节。最后,第十节本文对研究方向进行了探讨和展望。
II. 相关工作
关于基于单目视觉的状态估计/里程计SLAM的学术工作非常广泛。值得注意的方法包括PTAM[1]、SVO[2]、LSD-SLAM[3]、DSO[5]和ORB-SLAM[4]。显然,尝试对任何方法进行全面回顾都无法完整。然而,在这一节中,我们跳过了关于只使用视觉的方法的讨论,而只专注于关于单目视觉惯性状态估计的最相关的结果。
处理视觉和惯性测量的最简单的方法是松耦合的传感器融合[11][12],其中IMU被视为一个独立的模块,用于辅助运动的视觉结构(sfm)获得的纯视觉位姿估计。融合通常由扩展卡尔曼滤波(EKF)完成,其中IMU用于状态传播,而视觉位姿用于更新。进一步说,紧耦合视觉惯性算法要么基于EKF[13]-[15],要么基于图优化[7][8][16][17],其中相机和IMU测量值是从原始测量水平联合优化的。一种流行的基于EKF的VIO方法是MSCKF[13][14]。MSCKF在状态向量中维护以前的几个摄像机位姿,并使用多个摄像机视图中相同特征的视觉测量来形成多约束更新。SR-ISWF[18][19]是MSCKF的扩展。它采用squareroot形式[20]实现单精度表示,避免了较差的数值性质。该方法采用逆滤波器进行迭代再线性化,使其与基于优化的算法相当。批量图优化或集束调整技术(BA)维护和优化所有测量值以获得最优状态估计。为了达到恒定的处理时间,流行的基于图的VIO方法[8][16][17]通常采用边缘化过去的状态和测量来优化最近状态的有界滑动窗口。由于对非线性系统迭代求解的计算要求很高,很少有基于图的非线性系统能够在资源受限的平台(如手机上)实现实时性能。
对于视觉测量处理,根据视差模型的定义,算法可分为直接法和间接法。直接法[2][3][21]最小化光度误差,而间接法最小化几何位移。直接法因其吸引区域小,需要很好的初始估计,而间接法在提取和匹配特征时需要额外的计算资源。间接法由于其成熟性和鲁棒性,在实际工程部署中得到了广泛的应用。然而,直接法更容易扩展到稠密建图,因为它们是直接在像素级别上操作的。
在实践中,IMU通常以比摄像机更高的速率获取数据。不同的方法被提出来处理高速率的IMU测量值。最简单的方法是在基于EKF的方法中使用IMU进行状态传播[11][13]。在图优化公式中,为了避免重复的IMU重复积分,提出了一种有效的方法,即IMU预积分(IMU pre-integration)。这种方法在[22]中首次提出的,它用欧拉角来参数化旋转误差。在我们先前的工作中[7],我们提出了一种流形上的IMU预积分旋转公式,利用连续IMU误差状态动力学推导了协方差传递方程。然而IMU偏置被忽略了。在[23]中通过增加后验IMU偏置校正,进一步改进了预积分理论。
精确的初始值对于引导任何单目VINS是至关重要的。在[8][24]中提出了一种利用短期IMU预积分相对旋转的线性估计器初始化方法。但是,该方法不对陀螺仪偏置进行建模,无法在原始投影方程中对现代传感器噪声进行建模。在实际应用中,当视觉特性远离传感器套件时,这会导致不可靠的初始化。在[25]中给出了单目视觉惯性初始化问题的一种封闭解。随后,在[26]中提出了对这种封闭形式的解决方案的扩展,增加了陀螺仪的偏置校准。这些方法依赖于长时间内IMU测量的双重积分,无法模拟惯性积分的不确定性。在[27]中,提出了一种基于SVO的重初始化和故障恢复算法。这是一种基于松耦合融合框架的实用方法。然而,需要额外的朝下的距离传感器来恢复度量尺度。在[17]中引入了一种建立在ORB-SLAM[4]上的初始化算法。给出了一组ORB-SLAM的关键帧,计算了视觉惯性全局BA的尺度、重力方向、速度和IMU偏置的初步估计。然而,尺度收敛所需的时间可能超过10秒。这可能会给需要在一开始就进行尺度估计的机器人导航任务带来问题。
VIO方法,不管它们所依赖的基本数学公式,在全局的平移和旋转中长期受到漂移的影响。为此,回环检测在长期操作中起着重要的作用。ORB-SLAM[4] 利用了词袋模型能够闭合回环并重用地图。回环检测之后进行7自由度(位置、方向和尺度)的位姿图优化。相对于单目VINS,由于IMU的加入,漂移只发生在4自由度,即三维平移,和围绕重力方向的旋转(偏航角)。因此,本文选择在最小四自由度设定下,优化具有回环约束的位姿图。
III. 概述
提出的单目视觉惯性状态估计器的结构如图2所示。该系统从测量预处理(IV)开始,在其中提取和跟踪特征,对两个连续帧间的IMU测量值进行预积分。初始化过程(V)提供了所有必要的值,包括姿态、速度、重力向量、陀螺仪偏置和三维特征位置,用于引导随后的基于非线性优化的VIO。VIO(VI)与重定位(VII)模块紧密地融合了预先积分的IMU测量、特征观测和回环重新检测到的特征。最后,位姿图优化模块(VIII)接受几何验证的重定位结果,并进行全局优化以消除漂移。VIO、重新定位和位姿图优化模块在多线程设置中同时运行。每个模块有不同的运行速度和实时保证,以确保在任何时候可靠运行。
我们现在对整篇论文中使用的符号和坐标系进行定义。我们认为 是世界坐标系(world frame)。重力方向与世界坐标系z轴对齐。
是世界坐标系(world frame)。重力方向与世界坐标系z轴对齐。 是本体坐标系(body frame),我们把它定义为与IMU坐标系相同。
是本体坐标系(body frame),我们把它定义为与IMU坐标系相同。 是相机坐标系(camera frame)。我们同时使用旋转矩阵R和Hamilton四元数q来表示旋转。我们主要在状态向量中使用四元数,也用旋转矩阵来表示三维向量的旋转。
是相机坐标系(camera frame)。我们同时使用旋转矩阵R和Hamilton四元数q来表示旋转。我们主要在状态向量中使用四元数,也用旋转矩阵来表示三维向量的旋转。 ,
, 表示从本体坐标系到世界坐标系的旋转和平移。
表示从本体坐标系到世界坐标系的旋转和平移。 表示获取第k个图像时的本体坐标系。
表示获取第k个图像时的本体坐标系。 表示获取第k个图像时的相机坐标系。⊗表示两个四元数之间的乘法运算。
表示获取第k个图像时的相机坐标系。⊗表示两个四元数之间的乘法运算。![g_w = [ 0 , 0 , g ]^T](http://img.inotgo.com/imagesLocal/202207/06/202207060557471394_36.gif) 是世界坐标系上的重力向量。最后,我们将(^)表示为某一具体量的噪声测量值或估计值。
是世界坐标系上的重力向量。最后,我们将(^)表示为某一具体量的噪声测量值或估计值。
IV. 测量预处理
本节介绍VIO的预处理步骤。对于视觉测量,我们跟踪连续帧之间的特征,并在最新帧中检测新特征。对于IMU测量,我们在两个连续帧之间做预积分。请注意,我们使用的低成本IMU的测量值受到偏置和噪声的影响。因此,我们在IMU预积分过程中特别考虑偏置。
A. 视觉处理前端
对于每一幅新图像,KLT稀疏光流算法对现有特征进行跟踪[29]。同时,检测新的角点特征[30]以保证每个图像特征的最小数目(100-300)。该检测器通过设置两个相邻特征之间像素的最小间隔来执行均匀的特征分布。二维特征首先是不失真的,然后在通过外点剔除后投影到一个单位球面上。利用基本矩阵模型的RANSAC算法进行外点剔除。
在此步骤中还选择了关键帧。我们有两个关键帧选择标准。第一是与上一个关键帧的平均视差。如果在当前帧和最新关键帧之间跟踪的特征点的平均视差超出某个特定阈值,则将该帧视为新的关键帧。请注意,不仅平移,旋转也会产生视差。然而,特征点无法在纯旋转运动中三角化。为了避免这种情况,在计算视差时我们使用陀螺仪测量值的短时积分来补偿旋转。请注意,此旋转补偿仅用于关键帧选择,而不涉及VINS公式中的旋转计算。为此,即使陀螺仪含有较大的噪声或存在偏置,也只会导致次优的关键帧选择结果,不会直接影响估计质量。另一个标准是跟踪质量。如果跟踪的特征数量低于某一阈值,我们将此帧视为新的关键帧。这个标准是为了避免跟踪特征完全丢失。
B. IMU预积分
IMU预积分是在[22]中首次提出的,它将欧拉角的旋转误差参数化。在我们先前的工作中[7],我们提出了一个流形上的IMU预积分旋转公式。该文利用连续时间的IMU误差状态动力学推导协方差传递函数,但忽略了IMU偏置。文[23]通过增加后验IMU偏置校正,进一步改进了预积分理论。本文通过引入IMU偏置校正,扩展了我们在前面工作[7]中提出的IMU预积分。
IMU的原始陀螺仪和加速度计测量结果 和
和 如下:
如下:
IMU测量值是在本体坐标系中测量的,它是平衡重力和平台动力的合力,并受到加速度偏置ba、陀螺仪偏置bw和附加噪声的影响。假设加速度计和陀螺仪测量值中的附加噪声为高斯噪声, ,
, 。加速度计偏置和陀螺仪偏置被建模为随机游走,其导数为高斯性的,
。加速度计偏置和陀螺仪偏置被建模为随机游走,其导数为高斯性的,  ,
, 。
。
给定对应于体坐标系 和
和 的两个时刻,位置、速度和方向状态可以在时间间隔
的两个时刻,位置、速度和方向状态可以在时间间隔![[t_k,t_{k+1}]](http://img.inotgo.com/imagesLocal/202207/06/202207060557471394_6.gif) 间,在世界坐标系下中通过惯性测量值传递:
间,在世界坐标系下中通过惯性测量值传递:
 是
是![[t_k,t_{k+1}]](http://img.inotgo.com/imagesLocal/202207/06/202207060557471394_6.gif) 时间间隔之间的持续时间。
时间间隔之间的持续时间。
可见,IMU状态传递需要坐标系bk的旋转、位置和速度。当这些起始状态改变时,我们需要重新传递IMU测量值。特别是在基于优化的算法中,每次调整位姿时,都需要在它们之间重新传递IMU测量值。这种传递策略在计算上要求很高。为了避免重新传递,我们采用了预积分算法。
将参考坐标系从世界坐标系转变为局部坐标系bk后,我们只能对线性的加速度 和角速度
和角速度 相关的部分进行预积分,如下所示:
相关的部分进行预积分,如下所示:

可以看出预积分项(6)能通过将bk视为参考帧的IMU测量值单独得到。  ,
, ,
, 只与
只与 和
和 中的IMU偏置有关,与其他状态无关。当偏置估计发生变化时,若偏置变化很小,我们将
中的IMU偏置有关,与其他状态无关。当偏置估计发生变化时,若偏置变化很小,我们将  ,
, ,
, 按其对偏置的一阶近似来调整,否则就进行重新传递。这种策略为基于优化的算法节省了大量的计算资源,因为我们不需要重复传递IMU测量值。
按其对偏置的一阶近似来调整,否则就进行重新传递。这种策略为基于优化的算法节省了大量的计算资源,因为我们不需要重复传递IMU测量值。
对于离散时间的实现,可以采用不同的数值积分方法,如欧拉积分、中点积分、RK4积分等。这里选择了欧拉积分来演示易于理解的过程(我们在代码中使用了中点积分)。
在开始时, ,
, 是0,
是0, 是单位四元数。α,β,γ在(6)中的平均值是如下逐步传递的。注意,增加的噪声项
是单位四元数。α,β,γ在(6)中的平均值是如下逐步传递的。注意,增加的噪声项 ,
, 是未知的,在实现中被视为零。这得到了预积分的估计值,标记为
是未知的,在实现中被视为零。这得到了预积分的估计值,标记为 :
:
i是在![[t_k, t_{k+1}]](http://img.inotgo.com/imagesLocal/202207/06/202207060557471394_6.gif) 中IMU测量值对应的离散时刻,δt是IMU测量值i和i+1之间的时间间隔。
中IMU测量值对应的离散时刻,δt是IMU测量值i和i+1之间的时间间隔。
然后讨论协方差传递问题。由于四维旋转四元数 被过参数化,我们将其误差项定义为围绕其平均值的扰动:
被过参数化,我们将其误差项定义为围绕其平均值的扰动:
其中 是三维小扰动。
是三维小扰动。
我们可以导出误差项的连续时间线性化方程(6):
 可以通过初始协方差
可以通过初始协方差 的一阶离散时间协方差更新递归计算:
的一阶离散时间协方差更新递归计算:
其中Q是噪声的对角线协方差矩阵 。
。
同时,  的一阶雅可比矩阵
的一阶雅可比矩阵 相对于
相对于 也可以用初始雅可比矩阵
也可以用初始雅可比矩阵 递归计算。
递归计算。
利用这个递推公式,得到协方差矩阵 和雅可比矩阵
和雅可比矩阵 。
。  、
、  、
、  关于偏置的一阶近似可以写为:
关于偏置的一阶近似可以写为:
其中 是
是 中的子块矩阵,其位置对应于
中的子块矩阵,其位置对应于 。
。 、
、 、
、 、
、 也使用同样的含义。当偏置估计发生轻微变化时,我们使用(12)近似校正预积分结果,而不重新传递。
也使用同样的含义。当偏置估计发生轻微变化时,我们使用(12)近似校正预积分结果,而不重新传递。
现在我们可以写下IMU测量模型所其对应的协方差 :
:
V.估计器初始化
单目紧耦合VIO是一个高度非线性的系统。由于单目相机无法直接观测到尺度,因此,如果没有良好的初始值,很难直接将这两种测量结果融合在一起。可以假设一个静止的初始条件来启动单目VINS估计器。然而,这种假设是不合适的,因为在实际应用中经常会遇到运动下的初始化。当IMU测量结果被大偏置破坏时,情况就变得更加复杂了。事实上,初始化通常是单目VINS最脆弱的步骤。需要一个鲁棒的初始化过程以确保系统的适用性。
我们采用松耦合的传感器融合方法得到初始值。我们发现纯视觉SLAM,或从运动中恢复结构(SfM),具有良好的初始化性质。在大多数情况下,纯视觉系统可以通过从相对运动方法(如八点法[32]或五点法[33]或估计单应性矩阵)中导出初始值来引导自己。通过对齐IMU预积分与纯视觉SfM结果,我们可以粗略地恢复尺度、重力、速度,甚至偏置。这足以引导非线性单目VINS估计器,如图4所示。
与在初始阶段同时估计陀螺仪和加速度计偏置的[17]相比,我们在初始阶段选择忽略加速度计偏置项。加速度计偏置与重力耦合,且由于重力向量相对于平台动力学的大量级,以及初始阶段相对较短,这些偏置项很难被观测到。我们以前的工作对加速度计偏置标定进行了详细的分析[34]。
A. 滑动窗口(Sliding Window)纯视觉SfM
初始化过程从纯视觉SfM估计相机尺度位姿(up-to-scale)和特征位置图开始。
我们保持了一个帧的滑动窗口来限制计算复杂度。首先,我们检查了最新帧与之前所有帧之间的特征对应。如果我们能在滑动窗口中的最新帧和任何其他帧之间,找到稳定的特征跟踪(超过30个跟踪特征)和足够的视差(超过20个的旋转补偿像素),我们使用五点法[33]恢复这两个帧之间的相对旋转和尺度平移。否则,我们将最新的帧保存在窗口中,并等待新的帧。如果五点算法成功的话,我们任意设置尺度,并对这两个帧中观察到的所有特征进行三角化。基于这些三角特征,采用PnP[35]来估计窗口中所有其他帧的姿态。最后,应用全局光束平差法(BA)[36]最小化所有特征观测的重投影误差。由于我们还没有任何世界坐标系的知识,我们将第一个相机坐标系 设置为SfM的参考坐标系。所有帧的位姿
设置为SfM的参考坐标系。所有帧的位姿 和特征位置表示相对于
和特征位置表示相对于 。假设摄像机和IMU之间有一个粗略测量的外部参数
。假设摄像机和IMU之间有一个粗略测量的外部参数 ,我们可以将姿态从相机坐标系转换到物体(IMU)坐标系。
,我们可以将姿态从相机坐标系转换到物体(IMU)坐标系。
其中s是匹配视觉结构与距离尺度的尺度参数,解出尺度参数是实现成功初始化的关键。
B. 视觉惯性校准
1)陀螺仪偏置标定:考虑窗口中连续两帧 和
和 ,我们从视觉sfM中得到旋转
,我们从视觉sfM中得到旋转 和
和 ,从IMU预积分得到的相对约束
,从IMU预积分得到的相对约束 。我们对陀螺仪偏置求IMU预积分项的线性化,并最小化以下代价函数:
。我们对陀螺仪偏置求IMU预积分项的线性化,并最小化以下代价函数:
其中B代表窗口的所有帧。利用第四部分导出的偏置雅可比,给出了 对陀螺仪偏置的一阶近似。这样,我们得到了陀螺仪偏置bw的初始校准。然后我们用新的陀螺仪偏置重新传递所有的IMU预积分项
对陀螺仪偏置的一阶近似。这样,我们得到了陀螺仪偏置bw的初始校准。然后我们用新的陀螺仪偏置重新传递所有的IMU预积分项 、
、 、
、 。
。
2)速度、重力向量和尺度初始化:在陀螺仪偏置初始化后,我们继续初始化导航的其他基本状态,即速度、重力向量和尺度:
其中, 是第k帧图像本体坐标系的速度,
是第k帧图像本体坐标系的速度, 是
是 坐标系中的重力向量,s是单目SfM到公制单位的尺度。
坐标系中的重力向量,s是单目SfM到公制单位的尺度。
考虑窗口中两个连续帧bk和bk+1,那么(5)可以写成:
我们可以将(14)和(17)合并成以下线性测量模型:
可以看出 ,
, ,
, ,
,  是从带尺度的单目视觉中得到的,
是从带尺度的单目视觉中得到的, 是两个连续帧之间的时间间隔。通过求解线性最小二乘问题:
是两个连续帧之间的时间间隔。通过求解线性最小二乘问题:
我们可以得到窗口中每一帧的本体坐标系速度,视觉参照系(·)c0的重力向量,以及尺度参数。
3)重力细化:通过约束量值,可以对原线性初始化步骤得到的重力向量进行细化。在大多数情况下,重力向量的大小是已知的。这导致重力向量只剩2个自由度。因此,我们在其切线空间上用两个变量重新参数化重力。参数化将重力向量表示为
其中g是已知的重力大小, 是表示重力方向的单位向量,b1和b2是跨越切平面的两个正交基,如图5所示,w1和w2分别是在b1和b2上的对应位移。通过算法1的叉乘运算,可以找到一组b1、b2。然后用
是表示重力方向的单位向量,b1和b2是跨越切平面的两个正交基,如图5所示,w1和w2分别是在b1和b2上的对应位移。通过算法1的叉乘运算,可以找到一组b1、b2。然后用
代替(17)中的g,并与其它状态变量一起求解w1和w2。此过程迭代到 收敛为止。
收敛为止。


4)完成初始化:经过对重力向量的细化,通过将重力旋转到z轴上,得到世界坐标系与摄像机坐标系c0之间的旋转 。然后我们将所有变量从参考坐标系
。然后我们将所有变量从参考坐标系 旋转到世界坐标系
旋转到世界坐标系 。本体坐标系的速度也将被旋转到世界坐标系。视觉SfM的变换矩阵将被缩放到度量单位。此时,初始化过程已经完成,所有这些度量值都将被输入到一个紧耦合的单目VIO中。
。本体坐标系的速度也将被旋转到世界坐标系。视觉SfM的变换矩阵将被缩放到度量单位。此时,初始化过程已经完成,所有这些度量值都将被输入到一个紧耦合的单目VIO中。
VI. 紧耦合单目VIO
在估计器初始化后,我们采用基于滑动窗口的紧耦合单目VIO进行高精度和鲁棒的状态估计。图3显示了滑动窗口的图示。
A. 公式
滑动窗口中的完整状态向量定义为:
其中 是捕获第k图像时的IMU状态。它包含了IMU在世界坐标系中的位置、速度和方向,以及在IMU本体坐标系中的加速度计偏置和陀螺仪偏置。n是关键帧的总数,m是滑动窗口中的特征总数,λl是第一次观测到第l个特征的逆深度。
是捕获第k图像时的IMU状态。它包含了IMU在世界坐标系中的位置、速度和方向,以及在IMU本体坐标系中的加速度计偏置和陀螺仪偏置。n是关键帧的总数,m是滑动窗口中的特征总数,λl是第一次观测到第l个特征的逆深度。
我们使用视觉惯性BA。我们最小化所有测量残差的先验和Mahalanobis范数之和,得到最大后验估计:
其中Huber范数[37]被定义为:
 和
和 分别是IMU和视觉测量的残差。残差的详细定义将在第六节的B和C中提出。B是所有IMU测量的集合,C是在当前滑动窗口中至少观察到两次的一组特征。
分别是IMU和视觉测量的残差。残差的详细定义将在第六节的B和C中提出。B是所有IMU测量的集合,C是在当前滑动窗口中至少观察到两次的一组特征。 是来自边缘化的先验信息。Ceres Solver[38]被用来解决这个非线性问题。
是来自边缘化的先验信息。Ceres Solver[38]被用来解决这个非线性问题。
B. IMU测量残差
考虑滑动窗口中连续两个帧 和
和 内的IMU测量,根据(13)中定义的IMU测量模型,预积分IMU测量的残差可以定义为:
内的IMU测量,根据(13)中定义的IMU测量模型,预积分IMU测量的残差可以定义为:
其中,![[\cdot ]_{xyz}](http://img.inotgo.com/imagesLocal/202207/06/202207060557471394_61.gif) 是提取四元数q的向量部分,以进行误差状态表示。
是提取四元数q的向量部分,以进行误差状态表示。  是四元数的三维误差状态表示。
是四元数的三维误差状态表示。![[\hat \alpha_{b_{k+1}}^{b_k}, \hat \beta_{b_{k+1}}^{b_k},\hat \gamma_{b_{k+1}}^{b_k}]^T](http://img.inotgo.com/imagesLocal/202207/06/202207060557471394_37.gif) 是在两个连续图像帧的间隔时间内使用仅包含噪声的加速度计和陀螺仪测量值预积分的IMU测量项。加速度计和陀螺仪偏置也包括在在线校正的剩余项中。
是在两个连续图像帧的间隔时间内使用仅包含噪声的加速度计和陀螺仪测量值预积分的IMU测量项。加速度计和陀螺仪偏置也包括在在线校正的剩余项中。
C. 视觉测量残差
与在广义图像平面上定义重投影误差的传统针孔相机模型相比,我们在单位球面上定义摄像机的测量残差。几乎所有类型相机的光学,包括广角、鱼眼或全向相机,都可以模拟为连接单位球体表面的单位射线。假设第l个特征在第i幅图像中被第一次观察到,第j幅图像中的特征观测的残差定义为:
其中![[u_l^{c_i},v_l^{c_i}]](http://img.inotgo.com/imagesLocal/202207/06/202207060557471394_58.gif) 是第一次观测到出现在第i图像中的第l个特征。
是第一次观测到出现在第i图像中的第l个特征。![[\hat u_l^{c_j},\hat v_l^{c_j}]](http://img.inotgo.com/imagesLocal/202207/06/202207060557471394_76.gif) 是在第j图像中对相同特征的观察。
是在第j图像中对相同特征的观察。 是利用摄像机内参将像素位置转换成单位向量的反投影函数。由于视觉残差的自由度是2,所以我们将残差向量投影到切平面上。如图6所示,b1、b2是在切平面
是利用摄像机内参将像素位置转换成单位向量的反投影函数。由于视觉残差的自由度是2,所以我们将残差向量投影到切平面上。如图6所示,b1、b2是在切平面 上的两个任意选择的正交基。我们可以很容易地找到一组b1、b2,如算法1所示。在(22)中使用的
上的两个任意选择的正交基。我们可以很容易地找到一组b1、b2,如算法1所示。在(22)中使用的 是正切空间中固定长度的标准协方差。
是正切空间中固定长度的标准协方差。

D. 边缘化
为了限制基于优化的VIO的计算复杂度,本文引入了边缘化。我们有选择地从滑动窗口中将IMU状态xK和特征λ1边缘化,同时将对应于边缘状态的测量值转换为先验。
如图7所示,当倒数第二帧是关键帧时,它将停留在窗口中,而最旧的帧与其相应的测量值被边缘化。但如果倒数第二帧是非关键帧,我们丢掉视觉测量值,保留连接到这个非关键帧的IMU测量值。为了保持系统的稀疏性,我们不会边缘化非关键帧的所有测量值。我们的边缘化方案旨在保持窗口中空间分离的关键帧。这确保了特征三角化有足够的视差,并且最大化了在大激励下获得加速度计测量值的概率。
边缘化是利用Schur补[39]进行的。我们基于与移除状态相关的所有边缘化测量值构造一个新的先验。新的先验项被添加到现有的先验项中。
我们确实注意到,边缘化导致了线性化点的早期固定,这可能导致次优估计结果。然而,由于小型漂移对于VIO来说是可以接受的,我们认为边缘化所造成的负面效果并不重要。
E. 摄像机速率状态估计的纯运动视觉惯性BA
对于计算能力较低的设备如手机,由于对非线性优化的计算要求很高,紧耦合单目VIO无法实现摄像机速率输出。为此,我们采用了一种轻量级的纯运动视觉惯性BA,以提升状态估计速率到相机速率(30Hz)。
纯运动单目视觉惯性BA的代价函数与(22)中单目VIO的代价函数相同。然而我们只对固定数量的最新IMU状态的姿态和速度进行了优化,而不是对滑动窗口中的所有状态进行优化。我们将特征深度、外部参数、偏置和旧的IMU状态这些不希望优化的状态作为常量来处理。我们使用所有的视觉和惯性测量来进行纯运动的BA。这导致了比单帧PnP方法更平滑的状态估计。图8显示了提出方法的插图。与在最先进的嵌入式计算机上可能导致超过50ms的完全紧耦合单目VIO不同,这种纯运动的视觉惯性BA只需大约5ms来计算。这使得低延迟的相机频率进行位姿估计对无人机和AR应用特别有利。
F. IMU前向传递以达到IMU速率状态估计
IMU测量的速度远高于视觉测量。虽然我们的VIO频率受到图像捕获频率的限制,但是我们仍然可以通过最近的IMU测量来直接传递最新的VIO估计,以达到IMU速率的性能。高频状态估计可以作为回环检测的状态反馈。利用这种IMU速率状态估计进行的自主飞行实验在第九节的D中给出。
G. 故障检测与恢复
虽然我们紧耦合的单目视觉对各种具有挑战性的环境和运动是鲁棒的。由于强烈的光照变化或剧烈的运动,故障仍然是不可避免的。主动故障检测和恢复策略可以提高系统的实用性。故障检测是一个独立的模块,它检测估计器的异常输出。我们目前使用以下标准进行故障检测:
1. 在最新帧中跟踪的特征数小于某一阈值;
2. 最近两个估计器输出之间的位置或旋转有较大的不连续性;
3. 偏置或外部参数估计有较大的变化;
一旦检测到故障,系统将切换回初始化阶段。一旦单目VIO被成功初始化,将新建一个独立的位姿图。
VII. 重定位
我们的滑动窗口和边缘化方案限制了计算的复杂性,但也给系统带来了累积漂移。更确切地说,漂移发生在全局三维位置(x,y,z)和围绕重力方向的旋转(yaw)。为了消除漂移,提出了一种与单目VIO无缝集成的紧耦合重定位模块。重定位过程从一个循环检测模块开始,该模块识别已经访问过的地方。然后建立回环检测候选帧和当前帧之间的特征级连接。这些特征的对应关系紧密地集成到单目VIO模块中,从而以最小计算代价得到无漂移状态估计。多个特征的多个观测直接用于重定位,从而提高了定位的精度和状态估计的平滑性。重定位过程如图9(a)所示。
A. 回环检测
我们利用DBoW2[6],一种最先进的词袋位置识别方法来进行回环检测。除了用于单目VIO的角点特征外,另外500个角点被检测并由BRIEF描述子[40]描述。额外的角点特征用于在回环检测中实现更好的召回率。描述子被视为用于查询可视化数据库的可视单词。DBoW 2在时间和空间一致性检查后返回回环检测候选帧。我们保留所有用于特征检索的BRIEF描述子,丢弃原始图像以减少内存消耗。
我们注意到,我们的单目VIO可以观测到滚动和俯仰角。因此,我们不需要依赖旋转不变性,例如ORB SLAM中使用的ORB特性。
B. 特征恢复
当检测到回路时,通过检索特征对应关系建立局部滑动窗口与回环候选帧之间的连接。通过BRIEF描述子匹配找到对应关系。直接描述子匹配可能会造成大量异常值。为此,我们使用两步进行几何异常值剔除,如图10所示。
1. 2D-2D:RANSAC[31]的基本矩阵检验。我们利用当前图像中检索到的特征的二维观测和回环候选图像进行基本矩阵检验。
2. 3D-2D:RANSAC的PNP检验。基于特征在局部滑动窗口中已知的三维位置,以及回环候选图像中的二维观测,进行PNP检验。
当内点超过一定阈值时,我们将该候选帧视为正确的循环检测并执行重定位。
C. 紧耦合重定位
重定位过程有效地使单目VIO(VI)维持的当前滑动窗口与过去的位姿图对齐。在重定位过程中,我们将所有回环帧的位姿作为常量。利用所有IMU测量值、局部视觉测量和从回环中提取特征对应值,共同优化滑动窗口。我们可以轻松地为回环帧v观察到的检索特征编写视觉测量模型,使其与VIO中的视觉测量相同,如(25)所示。唯一的区别是,从位姿图(VIII)或直接从上一个里程计的输出(如果这是第一次重定位)获得的回环帧的姿态 被视为常数。为此,我们可以在(22)中稍微修改非线性代价函数,增加回环项:
被视为常数。为此,我们可以在(22)中稍微修改非线性代价函数,增加回环项:
其中L是回环帧中检索到的特征的观测集。(l,v) 是指在回环帧v中观察到的第l个特征。虽然代价函数与(22)略有不同,但待解状态的维数保持不变,因为回环帧的构成被视为常数。当用当前滑动窗口建立多个回环时,我们同时使用来自所有帧的所有回环特征对应进行优化。这就为重定位提供了多视角的约束,从而提高了定位的精度和平滑性。请注意,过去的姿态和回环帧的全局优化发生在重定位之后,将在第八节中讨论。
VIII. 全局位姿图优化
重新定位后,局部滑动窗口移动并与过去的位姿对齐。利用重定位结果,开发了额外的位姿图优化步骤,以确保过去位姿集注册到全局一致的配置中。
由于视觉惯性的建立使翻滚角和俯仰角完全可观测,累积漂移只发生在四个自由度(x,y,z和yaw)。为此,我们忽视对无漂移翻滚和俯仰状态的估计,只进行了四自由度位姿图的优化。
A. 在位姿图中添加关键帧
当关键帧从滑动窗口被边缘化时,它将被添加到位姿图中。这个关键帧在位姿图中作为顶点,它通过两种类型的边与其他顶点连接:
1)顺序边(Sequential Edge):关键帧将建立与之前关键帧的若干顺序边。顺序边表示局部滑动窗口中两个关键帧之间的相对转换,其值直接从VIO中获取。考虑到新边缘化的关键帧i及其先前的一个关键帧j,顺序边只包含相对位置和偏航角。
2)回环边(Loop Closure Edge):如果新边缘化的关键帧有一个回环连接,它将与回环帧通过一个回环边在位姿图图中连接。同样,闭环边缘只包含与(27)相同定义的四自由度相对位姿变换。回环边的值由重定位结果得出。
B. 4自由度位姿图优化
我们将帧i和j之间边的残差定义为:
其中,  ,
, 是直接从单目VIO中得到的翻滚角和俯仰角的估计。
是直接从单目VIO中得到的翻滚角和俯仰角的估计。
通过最小化以下代价函数,对顺序边和回环边的整个图进行优化:
其中S是所有顺序边的集合,L是回环边的集合。尽管紧耦合的重定位已经有助于消除错误的回环,但我们添加了另一个Huber范数 ρ(·),以进一步减少任何可能的错误回环的影响。相反,我们不对顺序边使用任何鲁棒范数,因为这些边是从VIO中提取出来的,VIO已经包含了足够多的外点排除机制。
位姿图优化和重定位(VII-C)异步运行在两个独立的线程中。以便在需要重定位时,能立即使用最优化的位姿图。同样,即使当前的位姿图优化尚未完成,仍然可以使用现有的位姿图配置进行重新定位。这一过程如图9(b)所示。
C. 位姿图管理
随着行程距离的增加,位姿图的大小可能会无限增长,从而限制了长时间系统的实时性。为此,我们实行了一个下采样过程,将位姿图数据库保持在有限的大小。所有具有回环约束的关键帧都将被保留,而其他与相邻帧过近或方向非常相似的关键帧可能会被删除。关键帧被移除的概率和其相邻帧的空间密度成正比。
IX. 实验结果
我们进行了三个实验和两个应用,以评估所提出的VINS-Mono系统。在第一个实验中,我们将提出的算法与另一种最先进算法在公共数据集上进行比较。我们通过数值分析以验证了系统的精度。然后在室内环境中测试我们的系统,以评估在重复场景中的性能。通过大量的实验验证了系统的长期实用性。此外,我们还将所提出的系统应用于两个应用。对于空中机器人的应用,我们使用VINS-Mono作为位置反馈来控制无人机跟踪预定的轨迹。然后我们将我们的方法移植到iOS移动设备上,并与Google Tango进行比较。
A. 数据集比较
我们使用EuRoC MAV视觉-惯性数据集[41]评估我们提出的VINS-Mono。这个数据集是在一架微型飞行器上收集的,它包含立体图像(Aptina MT9V034全局快门、WVGA单色、20 FPS)、同步IMU测量(ADIS 16448、200 Hz)和地面真实状态(Vicon和Leica MS 50)。我们只使用左边相机的图像。在这数据集中会观察到较大的IMU偏置和光照变化。
在这些实验中,我们将VINS-Mono和OKVIS进行了比较,这是一种最先进的单目和立体相机VIO。OKVIS是另一种基于优化的滑动窗口算法。我们的算法与OKVIS在许多细节上是不同的,如技术部分所示。我们的系统具有良好的初始化和回环功能。我们使用MH_03_median和MH_05_difficult两组序列来证明该方法的性能。为了简化表示,我们使用VINS来表示我们只使用单目VIO的方法,而VINS_loop表示含重定位和位姿图优化的完全版本。我们分别用OKVIS_Mono和OKVIS_stereo表示OKVIS使用单目和立体图像的结果。为了进行公平的比较,我们丢弃前100个输出,并使用接下来的150个输出对齐地面真值,并比较其余的估计器输出。
MH_03_median序列轨迹如图11所示。我们只比较平移误差,因为旋转运动在这个序列中是可以忽略的。图12显示了x、y、z误差与时间的关系,以及平移误差与距离的关系。在误差图中,具有回环的VINS-Mono具有最小的平移误差。我们在MH_05_difficult上观察到类似的结果。该方法具有最小的平移误差。平移和旋转误差如图14所示。由于该序列运动平稳,偏角变化不大,只发生位置漂移。显然,回环闭合有效地约束了累积漂移。OKVIS在翻滚角和俯仰角估计方面表现更好。一个可能的原因是VINS-Mono采用了预积分技术,即IMU传递的一阶近似,以节省计算资源。
VINS-Mono在所有Euroc数据集中都表现良好,即使在最具挑战性的序列V1_03_difficult中,它具有剧烈性的运动、纹理较少的区域和显著的光照变化。由于采用了专用的初始化过程,该方法可以在V1_03_difficult快速初始化。
对于纯VIO,VINS-Mono和OKVIS具有相似的精度,很难区分哪个比较好。然而,VINS-Mono在系统级别上优于OKVIS。它是一个完整的系统,具有鲁棒的初始化和回环闭合功能来辅助单目视觉。

B. 室内实验
在室内实验中,我们选择实验室环境作为实验区域。我们使用的传感器套件如图15所示。它搭载在DJI A3控制器上,包含一个单目照相机(20Hz)和一个IMU(100 Hz)。我们手握传感器套件,在实验室以正常的速度行走。如图16所示,我们遇到行人,光线较弱的位置,纹理较少的区域,玻璃和反射。多媒体附件中可以找到视频。

我们将我们的结果与OKVIS进行了比较,如图17所示。图17(a)是OKVIS的VIO输出。图17(b)是所提出的无回环方法的VIO结果。图17是所提出的具有重定位和回环闭合的方法的结果。当我们在室内转圈时,会出现明显的漂移。OKVIS和只有VIO版本的VINS-Mono在x、y、z和偏航角上积累了大量漂移。我们的重定位和回环闭合模块有效地消除了所有这些漂移。
C. 大范围环境
1)走出实验室:我们在室内和室外混合环境中测试VINS-Mono。传感器套件与图15所示的相同。我们从实验室的一个座位上开始,在室内空间里走来走去。然后我们下楼,在大楼外的操场上走来走去。接下来,我们回到楼里并上楼。最后,我们回到了实验室的同一个座位。整个轨迹超过700米,持续约10分钟。在多媒体附件中可以找到实验的视频。
轨迹如图19所示。图19(a)是OKVIS的轨迹。当我们上楼时,OKVIS显示出不稳定的特征跟踪,导致估计错误。我们看不到红色街区楼梯的形状。VINS-Mono的纯VIO结果如图19(b)所示。有闭环的轨迹如图19所示。该方法的楼梯形状清晰。为验证其准确性,将闭环轨迹与谷歌地图对齐,如图18所示。

OKVIS的 x、y和z轴的最终漂移为[13.80,-5.26,7.23]米。VINS-Mono无环闭路的最终漂移为[-5.47,2.76,-0.29]m,占整个轨迹长度的0.88%,小于OKVIS的2.36%。经回环修正,最终漂移上界为[-0.032,0.09,-0.07]m,与整个轨迹长度相比这是微不足道的。虽然我们没有地面真值,但我们仍然可以直观地检查优化后的轨迹是否平滑并能精确地与卫星地图对齐。
2)环游校园:这张环绕整个科大校园的非常大规模的数据集是用一个手持的VI-Sensor 4记录下来的。该数据集覆盖的地面长度约为710米,宽度为240米,高度变化为60米。总路径长度为5.62km。数据包含25Hz图像和200Hz IMU,持续1小时34分钟。对VINS-Mono的稳定性和耐久性进行测试是一个非常有意义的实验。
在这个大规模的测试中,我们将关键帧数据库的大小设置为2000,以提供足够的回环信息并达到实时性。我们运行此数据集时,采用英特尔i7-4790 CPU运行在3.60GHz。时间统计数据显示在表I中。如图20,估计的轨迹与谷歌地图一致。与谷歌地图相比,我们的结果在这个非常长时间的测试中几乎没有漂移。

D. 应用1:航空机器人的反馈控制
如图21(a)所示,我们将VINS-Mono应用于航空机器人的自主反馈控制。我们使用了一个具有752×480分辨率的前向全局曝光相机(MatrixVisionMvBlueFOXMLC200w),并配备了190度鱼眼镜头。DJIA3飞行控制器用于IMU测量和姿态稳定控制。机载计算资源是Intel i7-5500 U CPU运行在3.00GHz。传统的针孔摄像机模型不适用于大视场摄像机。我们使用MEI[42]模型,由[43]介绍的工具包进行校准。
在本实验中,我们测试使用VINS_Mono的状态估计来进行自主轨迹跟踪的性能。实验中回环检测被禁止。四旋翼被命令跟踪一个八字形图案,每个圆圈半径为1.0米,如图21(b)所示。在轨迹周围设置了四个障碍物,以验证VINS-Mono无闭环的准确性。在实验过程中,四旋翼连续四次跟踪这一轨迹。100 Hz机载状态估计(VI-F)支持对四旋翼的实时反馈控制。
地面真值是用OptiTrack 5获得的。总轨迹长度为61.97 m。最终漂移为[0.08,0.09,0.13]m,为0.29%的位置漂移。平移和旋转的细节以及它们相应的误差如图23所示。


E. 应用2:移动设备
我们将VINS-Mono移植到移动设备上,并提供一个简单的AR应用程序来展示其准确性和鲁棒性。我们将我们的移动实现命名为VINS-Mobile6,并将其与Google Tango Device 7进行了比较,后者是移动平台在商业上最好的增强现实解决方案之一。
VINS-Mono运行在iPhone7 Plus上。我们使用iPhone采集的30 Hz、分辨率为640×480的图像,以及内置InvenSense MP67B 6轴陀螺仪和加速度计获得的100 Hz 的IMU数据。如图24所示,我们将iPhone与一个启用Tango功能的联想Phab 2 Pro一起安装。Tango设备使用全局快门、鱼眼相机和同步IMU进行状态估计。首先,我们在从估计的视觉特征中提取出来的平面上插入一个虚拟立方体,如图25(a)所示。然后,我们拿着这两个装置,以正常的速度在房间内外行走。当检测到回环时,我们使用四自由度位姿图优化(VIII-B),以消除x,y,z和yaw漂移。

有趣的是,当我们打开一扇门时,Tango的偏航角估计会跳转到一个很大的角度,如图25(b)所示。其原因可能是由于不稳定的特征跟踪或主动故障检测和恢复而导致的估计器崩溃。然而,VINS-Mono在这个具有挑战性的情况中仍然表现很好。行走了大约264米后我们回到起点。最后的结果可以在图25( c)中看到,Tango的轨迹在最后一圈会漂移,而我们的VINS会回到起点。四自由度位姿图的优化消除了总轨迹的漂移。这与开始相比,立方体被标记到图像上的同一位置也印证了这一点。
诚然,尤其是对局部状态的估计,Tango比我们的实现更准确。但是实验结果表明,我们的方法可以在通用移动设备上运行,并且具有媲美特殊工程设备的潜力。实验还证明了该方法的鲁棒性。视频可以在多媒体附件中找到。
X. 结论和未来工作
本文提出了一种鲁棒、通用的单目视觉惯性估计器。我们的方法在IMU预积分,估计器初始化和故障恢复,在线外部校准,紧耦合视觉惯性里程计,重定位和有效的全局优化上,具有最先进的和新颖的解决方案。我们通过与最先进的开源实现和高度优化的行业解决方案进行比较,显示出更好的性能。我们开源了PC和iOS的实现,以造福社会。
虽然基于特征的VINS估计器已经达到了实际使用的成熟程度,我们仍然看到了未来研究的许多方向。单目VINS可能会根据运动和环境而达到较难观测甚至退化的状态。我们最感兴趣的是在线方法来评估单目VINS的可观测性,以及在线生成运动计划来恢复可观测性。另一个研究方向是在大量消费设备上大规模部署单目VINS,例如移动电话。这一应用要求在线校准几乎所有传感器的内参和外参,以及在线鉴定校准质量。最后,我们感兴趣的是制作由单目VINS给出的稠密地图。我们在[44]中首次给出了用于无人机导航的单目视觉-惯性稠密地图的结果。然而,仍需进行广泛的研究以进一步提高系统的精度和鲁棒性。
边栏推荐
- Web服务连接器:Servlet
- Jushan database appears again in the gold fair to jointly build a new era of digital economy
- Detailed explanation of BF and KMP
- CoDeSys note 2: set coil and reset coil
- 清除浮动的方式
- Zoom through the mouse wheel
- As3013 fire endurance test of cable distribution system
- HCIA review
- Rustdesk builds its own remote desktop relay server
- 授予渔,从0开始搭建一个自己想要的网页
猜你喜欢
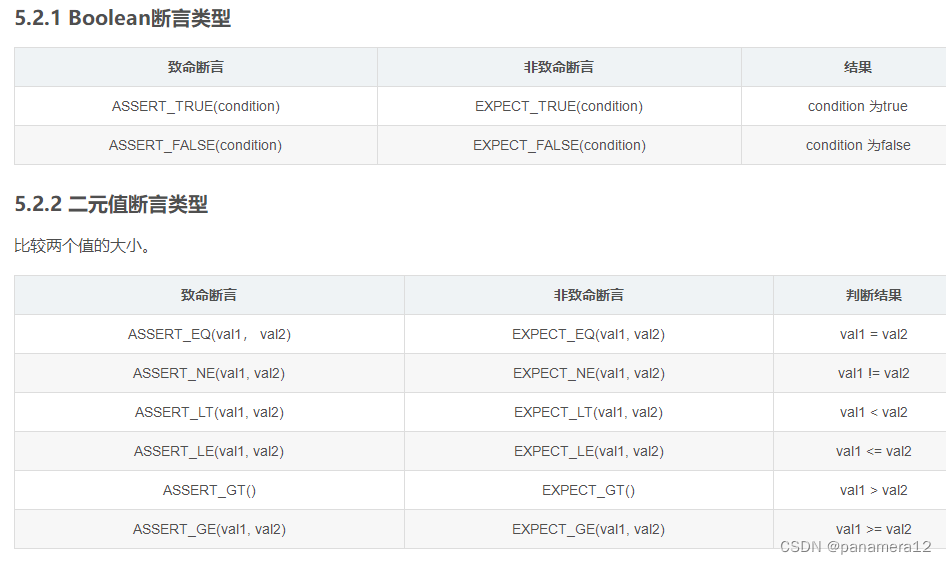
Usage of test macro of GTEST

LAN communication process in the same network segment

The ECU of 21 Audi q5l 45tfsi brushes is upgraded to master special adjustment, and the horsepower is safely and stably increased to 305 horsepower
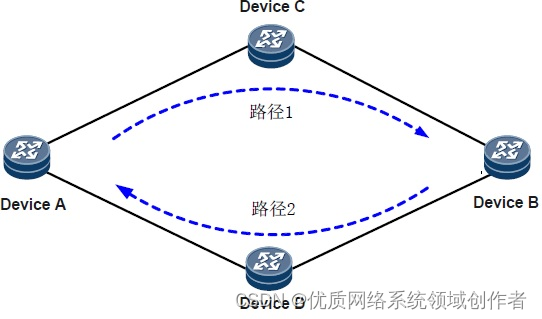
Huawei BFD configuration specification
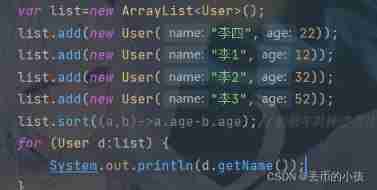
Arrays and collections

Li Chuang EDA learning notes 12: common PCB board layout constraint principles
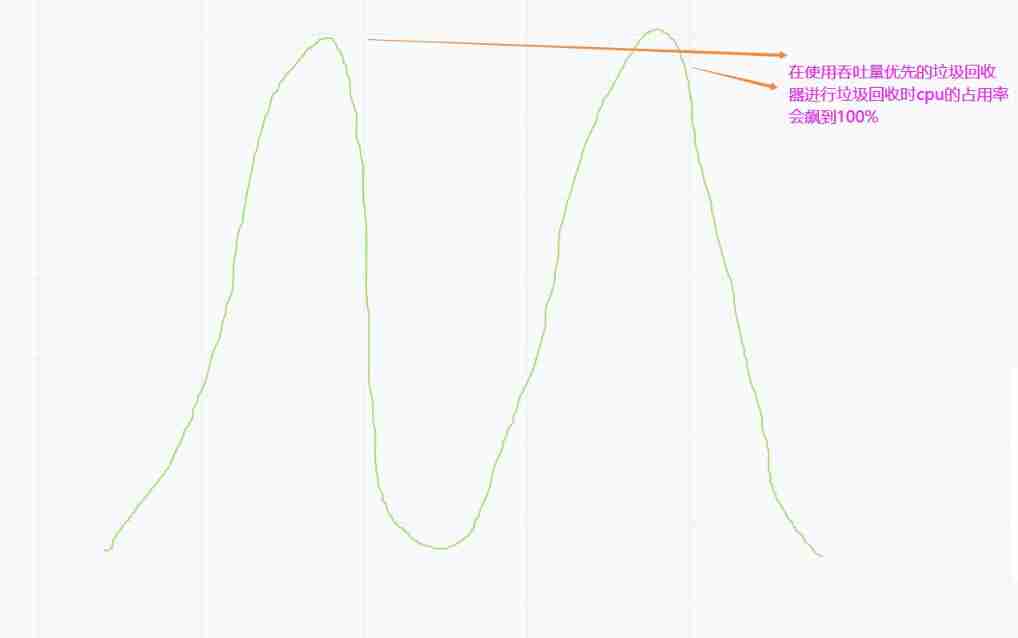
Garbage collector with serial, throughput priority and response time priority
C language bubble sort
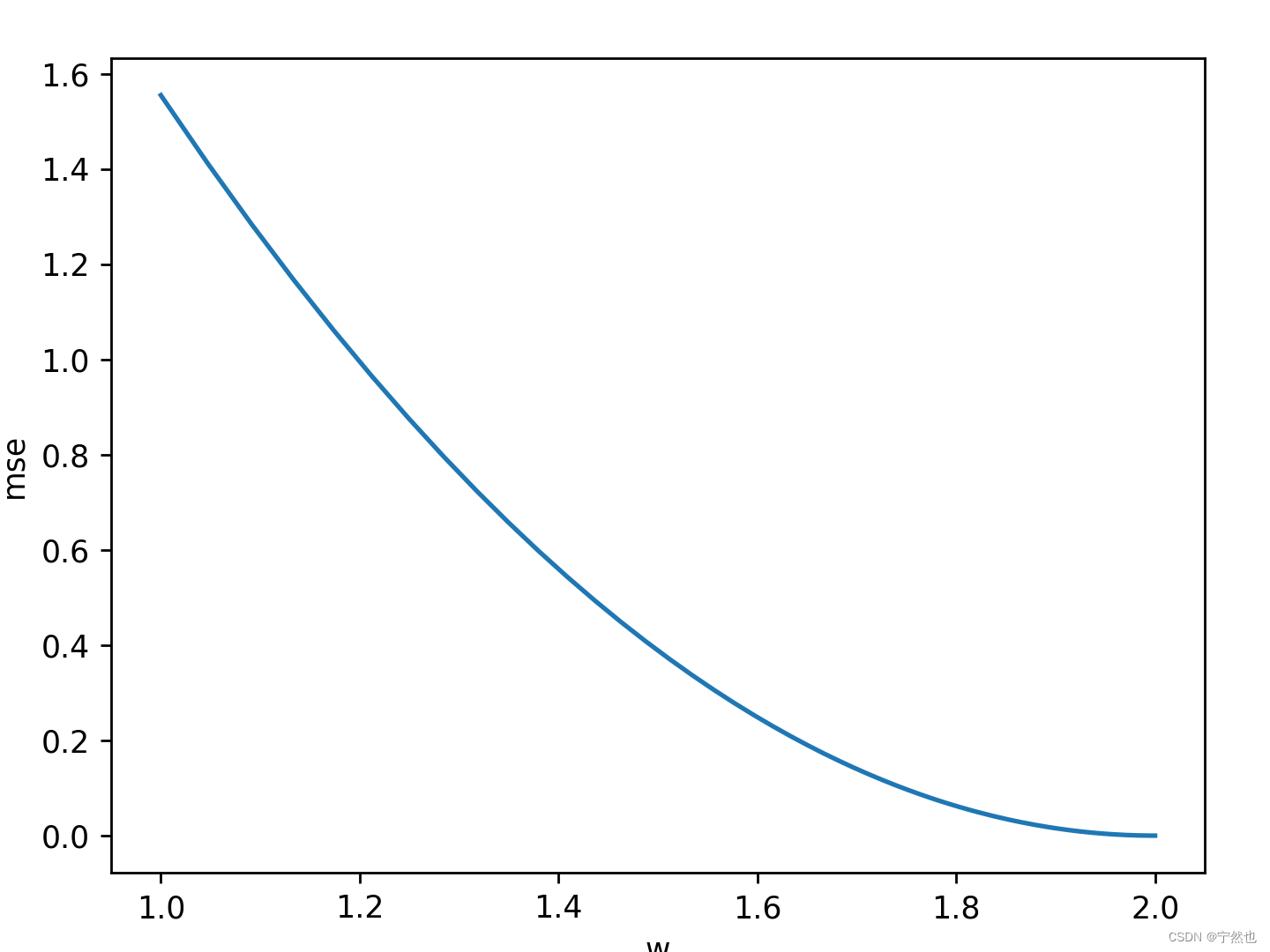
B站刘二大人-线性回归及梯度下降
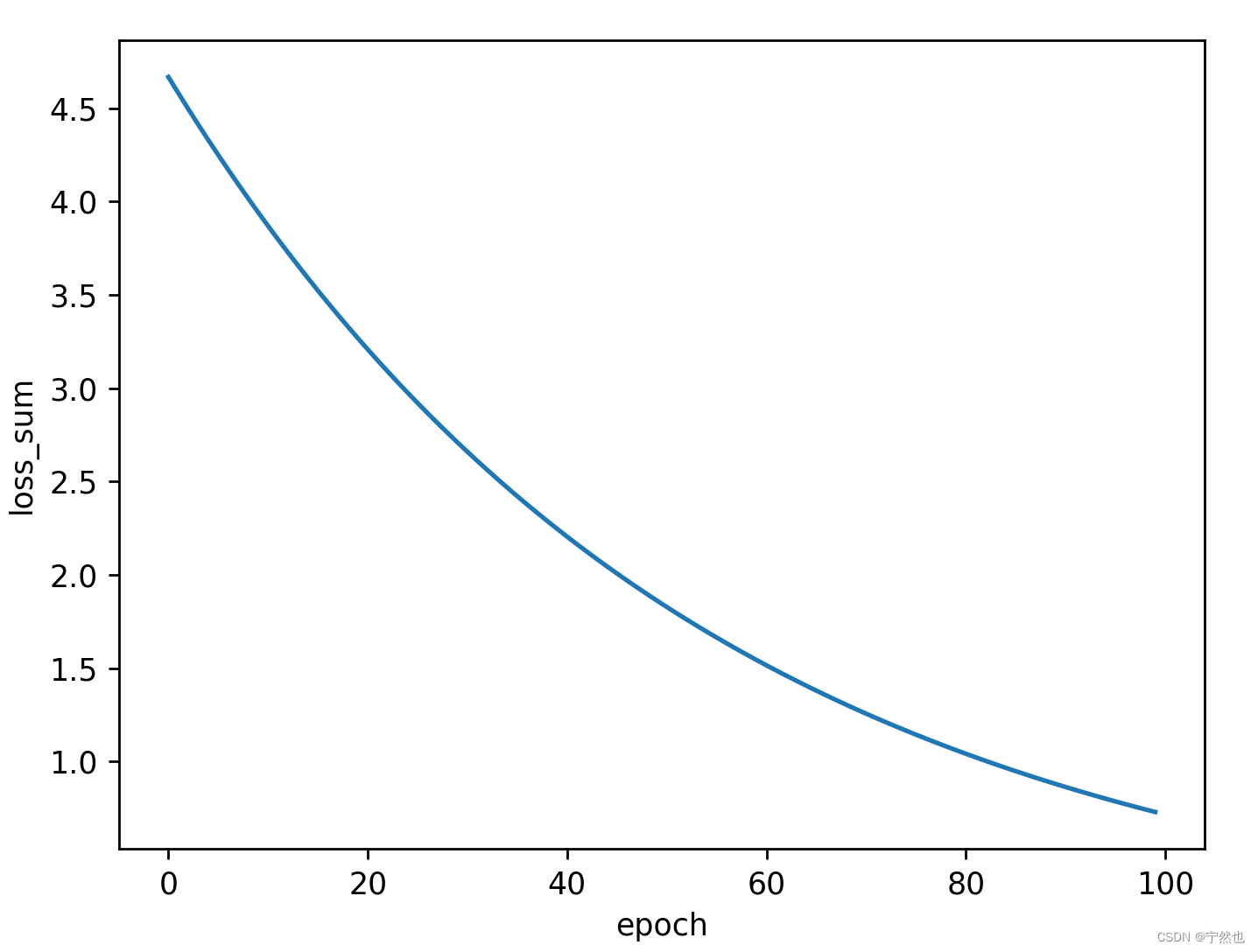
Station B, Master Liu Er - back propagation
随机推荐
Garbage collector with serial, throughput priority and response time priority
The usage and difference between strlen and sizeof
養了只小猫咪
ArcGIS application foundation 4 thematic map making
Baidu online AI competition - image processing challenge: the 8th program of handwriting erasure
LTE CSFB process
A master in the field of software architecture -- Reading Notes of the beauty of Architecture
The ECU of 21 Audi q5l 45tfsi brushes is upgraded to master special adjustment, and the horsepower is safely and stably increased to 305 horsepower
YYGH-11-定时统计
如何在业务代码中使用 ThinkPHP5.1 封装的容器内反射方法
通讯录管理系统链表实现
Gtest之TEST宏的用法
AUTOSAR从入门到精通番外篇(十)-嵌入式S19文件解析
MIT6.s081-2020 Lab2 System Calls
Hongliao Technology: how to quickly improve Tiktok store
[Jiudu OJ 07] folding basket
[experience] install Visio on win11
c语言——冒泡排序
入侵检测领域数据集总结
【SQL server速成之路】——身份驗證及建立和管理用戶賬戶