当前位置:网站首页>Tree-LSTM的一些理解以及DGL代码实现
Tree-LSTM的一些理解以及DGL代码实现
2022-07-06 10:26:00 【Icy Hunter】
前言
Tree-LSTM其实在好久之前就研究过了,那也应该是我第一次学DGL的时候。因为树就是一种特殊的图,也算是我入门图神经网络的基础操作,依稀记得当时搞着模型也是弄了蛮久的…
Tree-LSTM
Tree-LSTM是一种树形结构的LSTM,能够提高LSTM计算的并行速度,同时能够融入依存树或者句法树的相关信息,从而达到比较好的句子建模的效果。
Tree-LSTM有两种形式,一种是N-ary Tree-LSTM还有一种是Child-sum Tree-LSTM,前者能够记录时序信息但对孩子节点的个数有特点限制,后者会失去位置信息,但是对孩子节点的个数没有要求。
LSTM
在理解两种Tree-LSTM前,可以回顾一下我们经典的LSTM: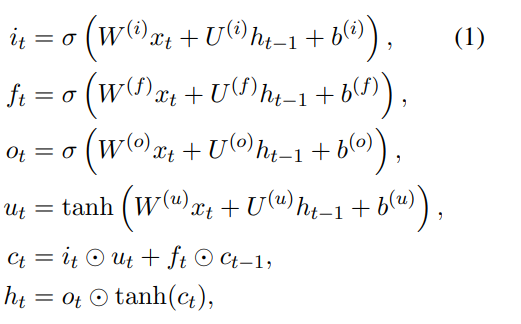
其中:
σ()、tanh()是激活函数
it是输入们得到的信息,xt 是输入的特征,W(i) 是对应输入门输入特征的变换矩阵,ht-1是前一个状态的隐藏层 U(i) 是输入门隐藏层的变换矩阵,b(i) 为输入门的偏置
ft是遗忘门得到的信息,xt 是输入的特征,W(f) 是对应遗忘门输入特征的变换矩阵,ht-1是前一个状态的隐藏层 U(f) 是遗忘门隐藏层的变换矩阵,b(f) 为遗忘门的偏置
ot是输出门得到的信息,xt 是输入的特征,W(o) 是对应输出门输入特征的变换矩阵,ht-1是前一个状态的隐藏层 U(o) 是输出门隐藏层的变换矩阵,b(o) 为遗忘门的偏置
ct为当前的细胞状态,⨀代表点积,即矩阵对应元素相乘
ht则是更新后的隐藏层
总的来说,公式还是比较简单的,因为没有Σ求和符号什么的,读懂公式的计算过程还是很容易的。
N-ary Tree-LSTM
N-ary Tree-LSTM即有N个孩子节点的Tree-LSTM,特点是能够较好的保留时序信息,不过对孩子节点的个数有限制要求,因此这种一般都为二叉树结构的输入,因为计算起来比较简单。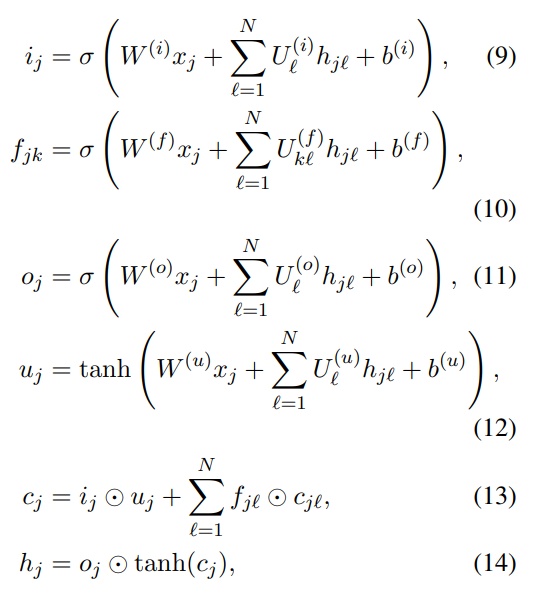
N-ary Tree-LSTM和经典的LSTM就是多了几个Σ求和符号。
如果N=2,那么意味着每个父节点的孩子节点数都为2,那么输入门、输出门、遗忘门中各自有两个U来对前一时刻对应两个孩子节点的隐藏层进行线性变换,然后求和,因为这操作分别对应左右两个孩子,因此是能够记录时序信息的。因为N=2是事先设定的,如果你的数据里出现了三个孩子节点的情况,那么就要报错了。
还是举个例子比较形象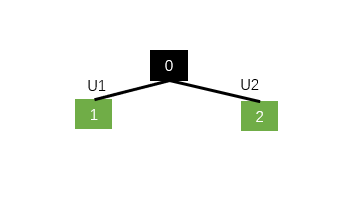
例如N=2,0为父节点,那么N-ary Tree-LSTM会在子节点1和2的位置中的三种门中分别设置一个隐藏层变换矩阵U1和U2,左节点就和U1计算,右节点就和U2计算,这样就保证位置信息能够得以保留,但是不能够解决数据中含有三叉及以上的情况。
Child-sum Tree-LSTM
Child-sum Tree-LSTM就比较简单了,顾名思义,他就是将子节点的隐藏层都求和然后再去更新父节点的隐藏层。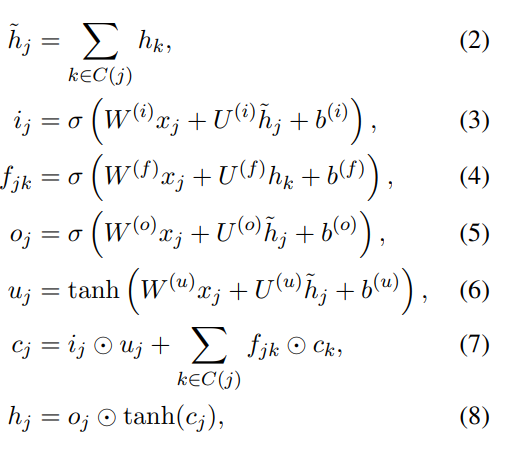
对比N-ary Tree-LSTM可以发现三个门中的Σ求和符号没了,因为(2)中将孩子节点的隐藏层直接求和,记为 h ~ \widetilde{h} hj,然后用它进去三门进行计算即可。因为这里是求和操作,那么孩子节点的个数就不受限制了,因为求和之后就相当于只有一个了,三门中只需要设置一个对应的U即可,但是缺点就是,求和之后,孩子节点的位置信息就失去了。
以及这里遗忘门是对每个孩子节点各自求一个遗忘信息,不过是共享参数U(f)
同样可以举个例子,例如此时N=3
如果是N-ary Tree-LSTM: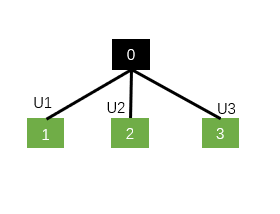
就要对应分别三组。
如果是Child-sum Tree-LSTM:
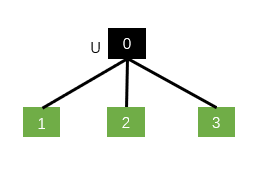
只需要一个就可以了,因为子节点都求和了。
DGL代码实现
N-ary Tree-LSTM
这个代码完全来自DGL官网。这里是一个对每个节点做预测的情感分类任务。
from collections import namedtuple
import dgl
from dgl.data.tree import SSTDataset
SSTBatch = namedtuple('SSTBatch', ['graph', 'mask', 'wordid', 'label'])
# Each sample in the dataset is a constituency tree. The leaf nodes
# represent words. The word is an int value stored in the "x" field.
# The non-leaf nodes have a special word PAD_WORD. The sentiment
# label is stored in the "y" feature field.
trainset = SSTDataset(mode='tiny') # the "tiny" set has only five trees
tiny_sst = trainset.trees
num_vocabs = trainset.num_vocabs
num_classes = trainset.num_classes
vocab = trainset.vocab # vocabulary dict: key -> id
inv_vocab = {
v: k for k, v in vocab.items()} # inverted vocabulary dict: id -> word
a_tree = tiny_sst[0]
for token in a_tree.ndata['x'].tolist():
if token != trainset.PAD_WORD:
print(inv_vocab[token], end=" ")
import torch as th
import torch.nn as nn
class TreeLSTMCell(nn.Module):
def __init__(self, x_size, h_size):
super(TreeLSTMCell, self).__init__()
self.W_iou = nn.Linear(x_size, 3 * h_size, bias=False)
self.U_iou = nn.Linear(2 * h_size, 3 * h_size, bias=False)
self.b_iou = nn.Parameter(th.zeros(1, 3 * h_size))
self.U_f = nn.Linear(2 * h_size, 2 * h_size)
def message_func(self, edges):
return {
'h': edges.src['h'], 'c': edges.src['c']}
def reduce_func(self, nodes):
# concatenate h_jl for equation (1), (2), (3), (4)
h_cat = nodes.mailbox['h'].view(nodes.mailbox['h'].size(0), -1)
# equation (2)
f = th.sigmoid(self.U_f(h_cat)).view(*nodes.mailbox['h'].size())
# second term of equation (5)
c = th.sum(f * nodes.mailbox['c'], 1)
return {
'iou': self.U_iou(h_cat), 'c': c}
def apply_node_func(self, nodes):
# equation (1), (3), (4)
iou = nodes.data['iou'] + self.b_iou
i, o, u = th.chunk(iou, 3, 1)
i, o, u = th.sigmoid(i), th.sigmoid(o), th.tanh(u)
# equation (5)
c = i * u + nodes.data['c']
# equation (6)
h = o * th.tanh(c)
return {
'h' : h, 'c' : c}
class TreeLSTM(nn.Module):
def __init__(self,
num_vocabs,
x_size,
h_size,
num_classes,
dropout,
pretrained_emb=None):
super(TreeLSTM, self).__init__()
self.x_size = x_size
self.embedding = nn.Embedding(num_vocabs, x_size)
if pretrained_emb is not None:
print('Using glove')
self.embedding.weight.data.copy_(pretrained_emb)
self.embedding.weight.requires_grad = True
self.dropout = nn.Dropout(dropout)
self.linear = nn.Linear(h_size, num_classes)
self.cell = TreeLSTMCell(x_size, h_size)
def forward(self, batch, h, c):
"""Compute tree-lstm prediction given a batch. Parameters ---------- batch : dgl.data.SSTBatch The data batch. h : Tensor Initial hidden state. c : Tensor Initial cell state. Returns ------- logits : Tensor The prediction of each node. """
g = batch.graph
# to heterogenous graph
g = dgl.graph(g.edges())
# feed embedding
embeds = self.embedding(batch.wordid * batch.mask)
g.ndata['iou'] = self.cell.W_iou(self.dropout(embeds)) * batch.mask.float().unsqueeze(-1)
g.ndata['h'] = h
g.ndata['c'] = c
# propagate
dgl.prop_nodes_topo(g,
message_func=self.cell.message_func,
reduce_func=self.cell.reduce_func,
apply_node_func=self.cell.apply_node_func)
# compute logits
h = self.dropout(g.ndata.pop('h'))
logits = self.linear(h)
return logits
from torch.utils.data import DataLoader
import torch.nn.functional as F
device = th.device('cpu')
# hyper parameters
x_size = 256
h_size = 256
dropout = 0.5
lr = 0.05
weight_decay = 1e-4
epochs = 10
# create the model
model = TreeLSTM(trainset.num_vocabs,
x_size,
h_size,
trainset.num_classes,
dropout)
print(model)
# create the optimizer
optimizer = th.optim.Adagrad(model.parameters(),
lr=lr,
weight_decay=weight_decay)
def batcher(dev):
def batcher_dev(batch):
batch_trees = dgl.batch(batch)
return SSTBatch(graph=batch_trees,
mask=batch_trees.ndata['mask'].to(device),
wordid=batch_trees.ndata['x'].to(device),
label=batch_trees.ndata['y'].to(device))
return batcher_dev
train_loader = DataLoader(dataset=tiny_sst,
batch_size=5,
collate_fn=batcher(device),
shuffle=False,
num_workers=0)
# training loop
for epoch in range(epochs):
for step, batch in enumerate(train_loader):
g = batch.graph
n = g.number_of_nodes()
h = th.zeros((n, h_size))
c = th.zeros((n, h_size))
logits = model(batch, h, c)
logp = F.log_softmax(logits, 1)
loss = F.nll_loss(logp, batch.label, reduction='sum')
optimizer.zero_grad()
loss.backward()
optimizer.step()
pred = th.argmax(logits, 1)
acc = float(th.sum(th.eq(batch.label, pred))) / len(batch.label)
print("Epoch {:05d} | Step {:05d} | Loss {:.4f} | Acc {:.4f} |".format(
epoch, step, loss.item(), acc))
Child-sum Tree-LSTM
可以看懂了N-ary再来看Child-sum的,差不太多。
import torch as th
import torch.nn as nn
class ChildSumTreeLSTMCell(nn.Module):
def __init__(self, x_size, h_size):
super(ChildSumTreeLSTMCell, self).__init__()
self.W_iou = nn.Linear(x_size, 3 * h_size, bias=False)
self.U_iou = nn.Linear(h_size, 3 * h_size, bias=False)
self.b_iou = nn.Parameter(th.zeros(1, 3 * h_size))
self.U_f = nn.Linear(h_size, h_size)
def message_func(self, edges):
return {
'h': edges.src['h'], 'c': edges.src['c']}
def reduce_func(self, nodes):
h_tild = th.sum(nodes.mailbox['h'], 1)
f = th.sigmoid(self.U_f(nodes.mailbox['h']))
c = th.sum(f * nodes.mailbox['c'], 1)
return {
'iou': self.U_iou(h_tild), 'c': c}
def apply_node_func(self, nodes):
iou = nodes.data['iou'] + self.b_iou
i, o, u = th.chunk(iou, 3, 1)
i, o, u = th.sigmoid(i), th.sigmoid(o), th.tanh(u)
c = i * u + nodes.data['c']
h = o * th.tanh(c)
return {
'h': h, 'c': c}
class TreeLSTM(nn.Module):
def __init__(self,
num_vocabs,
x_size,
h_size,
num_classes,
dropout,
pretrained_emb=None):
super(TreeLSTM, self).__init__()
self.x_size = x_size
self.embedding = nn.Embedding(num_vocabs, x_size)
if pretrained_emb is not None:#这里可以使用预训练词向量
print('Using glove')
self.embedding.weight.data.copy_(pretrained_emb)
self.embedding.weight.requires_grad = True
self.dropout = nn.Dropout(dropout)
self.linear = nn.Linear(h_size, num_classes)
self.cell = ChildSumTreeLSTMCell(x_size, h_size)
def forward(self, batch, h, c):
"""Compute tree-lstm prediction given a batch. Parameters ---------- batch : dgl.data.SSTBatch The data batch. h : Tensor Initial hidden state. c : Tensor Initial cell state. Returns ------- logits : Tensor The prediction of each node. """
# print("batch", batch)
g = batch.graph
# print("g", g)
# to heterogenous graph
g = dgl.graph(g.edges())
# feed embedding
embeds = self.embedding(batch.wordid * batch.mask)
#叶子节点没有入度,因此message_func和reduce_func都可以忽略,直接apply_node_func
g.ndata['iou'] = self.cell.W_iou(self.dropout(embeds)) * batch.mask.float().unsqueeze(-1)
g.ndata['h'] = h
g.ndata['c'] = c
g.ndata['node_pos'] = batch.node_pos
# print(type(batch.wordid))
# prop_nodes_topo是根据我们指定的拓扑顺序来进行消息传递
dgl.prop_nodes_topo(g,
message_func=self.cell.message_func,
reduce_func=self.cell.reduce_func,
apply_node_func=self.cell.apply_node_func)
# compute logits
# print("after_prop_nodes_topo", g)
h = self.dropout(g.ndata.pop('h'))
pos = g.ndata["node_pos"]
pos_sen = torch.nonzero(pos==0).squeeze() # 0的位置为根节点
sen_hidden = h[pos_sen]
logits = self.linear(sen_hidden)
return logits
child_sum_Tree_LSTM = TreeLSTM(100, 50, 50, 2, 0.2)
print(child_sum_Tree_LSTM)
参考
2015-Tree-LSTM-Improved Semantic Representations From Tree-Structured Long Short-Term Memory Networks
https://docs.dgl.ai/tutorials/models/2_small_graph/3_tree-lstm.html#sphx-glr-tutorials-models-2-small-graph-3-tree-lstm-py
边栏推荐
- win10系统下插入U盘有声音提示却不显示盘符
- TOP命令详解
- MSF horizontal MSF port forwarding + routing table +socks5+proxychains
- 二分(整数二分、实数二分)
- 2022 Summer Project Training (III)
- Stealing others' vulnerability reports and selling them into sidelines, and the vulnerability reward platform gives rise to "insiders"
- 【Swoole系列2.1】先把Swoole跑起来
- 华为0基金会——图片整理
- Principle and usage of extern
- node の SQLite
猜你喜欢

Recursive way
Olivetin can safely run shell commands on Web pages (Part 1)
Easy to use PDF to SVG program
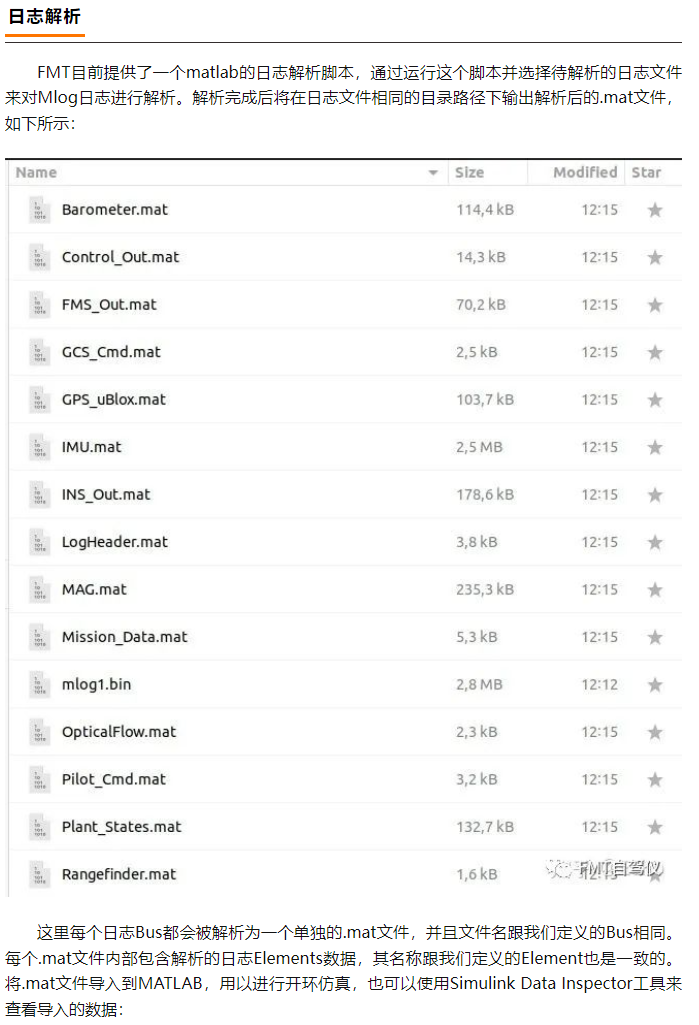
FMT open source self driving instrument | FMT middleware: a high real-time distributed log module Mlog
C language exchanges two numbers through pointers
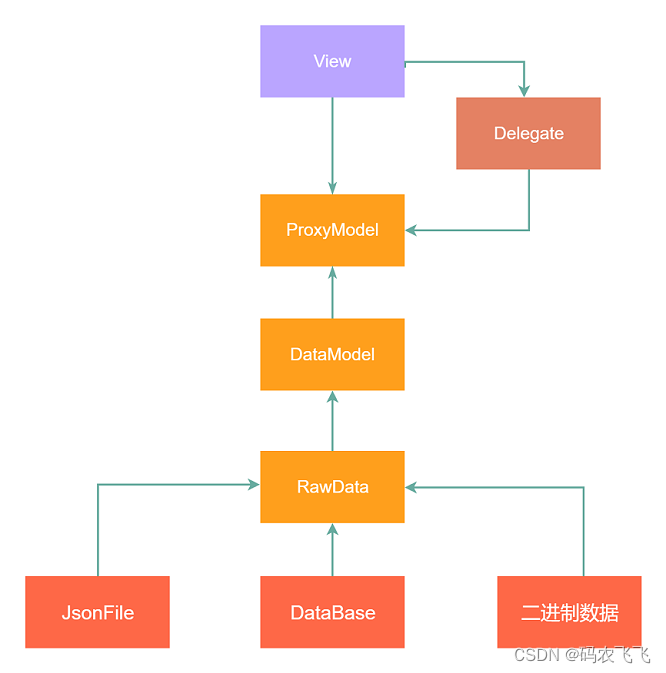
QT中Model-View-Delegate委托代理机制用法介绍
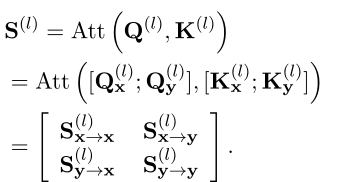
从交互模型中蒸馏知识!中科大&美团提出VIRT,兼具双塔模型的效率和交互模型的性能,在文本匹配上实现性能和效率的平衡!...
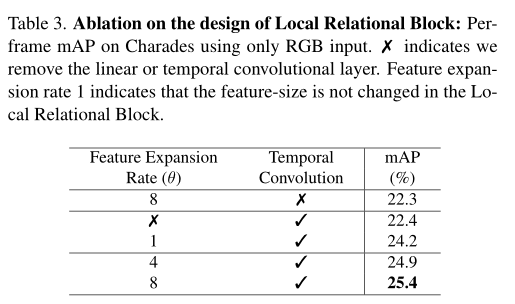
Ms-tct: INRIA & SBU proposed a multi-scale time transformer for motion detection. The effect is SOTA! Open source! (CVPR2022)...
【Swoole系列2.1】先把Swoole跑起来
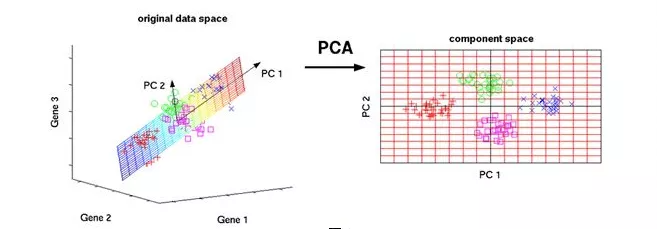
30 分钟看懂 PCA 主成分分析
随机推荐
Declval of template in generic programming
Insert dial file of Jerry's watch [chapter]
Take you through ancient Rome, the meta universe bus is coming # Invisible Cities
编译原理——自上而下分析与递归下降分析构造(笔记)
TOP命令详解
STM32+ESP8266+MQTT协议连接OneNet物联网平台
STM32+MFRC522完成IC卡号读取、密码修改、数据读写
重磅硬核 | 一文聊透对象在 JVM 中的内存布局,以及内存对齐和压缩指针的原理及应用
30 分钟看懂 PCA 主成分分析
Principle and usage of extern
2022暑期项目实训(二)
Jerry's access to additional information on the dial [article]
UDP protocol: simple because of good nature, it is inevitable to encounter "city can play"
华为0基金会——图片整理
Interview shock 62: what are the precautions for group by?
[Android] kotlin code writing standardization document
【.NET CORE】 请求长度过长报错解决方案
Declval (example of return value of guidance function)
Markdown grammar - better blogging
测试1234