当前位置:网站首页>PAT Grade A 1143 Lowest Common Ancestor
PAT Grade A 1143 Lowest Common Ancestor
2022-08-02 17:04:00 【Keyboard sonata】
The lowest common ancestor (LCA) of two nodes U and V in the tree is the deepest node that has both U and V as descendants.
A binary search tree (BST) is recursively defined as a binary tree with the following properties:
If its left subtree is not empty, the value of all nodes in the left subtree is less than the value of its root node
If its right subtree is not empty, then all nodes in the right subtreeThe value of a point is greater than or equal to the value of its root node
Its left and right subtrees are also binary search trees
Now given any two nodes in the BST, please find outtheir lowest common ancestor.Input format
The first line contains two integers M and N, which represent the number of query node pairs and the number of nodes in the binary search tree, respectively.The second line contains N distinct integers representing the sequence of preorder traversal of the binary search tree.
The next M lines, each containing two integers U and V, represent a set of queries.
All node weights are in the range of int.
Output format
For each given pair of U and V, output one line of results.If the LCA of U and V is A, and A is not U or V, output LCA of U and V is A.
If the LCA of U and V is A, and A is one of U or V, output X is an ancestor of Y., where X represents A and Y represents the other node.
If U or V is not found in BST, output ERROR: U is not found. or ERROR: V is not found. or ERROR: U and V are not found..
Data Range
1≤M≤1000,
1≤N≤10000
Input example:
6 8
6 3 1 2 5 4 8 7
2 5
8 7
1 9
12 -3
0 8
99 99
Sample output:
LCA of 2 and 5 is 3.
8 is an ancestor of 7.
ERROR: 9 is not found.
ERROR: 12 and -3 are not found.
ERROR: 0 is not found.
ERROR: 99 and 99 are not found.
My solution:
#include using namespace std;const int N = 1000010;int m, n;int pre[N], in[N], f[N], dep[N];unordered_map pos;int build(int il, int ir, int pl, int pr, int d){int root = pre[pl];int k = pos[root];dep[root] = d;if(il < k) f[build(il, k - 1, pl + 1, pl + 1 + k - 1 - il, d + 1)] = root;if(k < ir) f[build(k + 1, ir, pl + 1 + k - il, pr, d + 1)] = root;return root;}int main(){cin >> m >> n;for(int i = 0; i < n; i ++ ){cin >> pre[i];in[i] = pre[i];}sort(in, in + n);for(int i = 0; i < n; i ++ ){pos[in[i]] = i;}int d = 0;build(0, n - 1, 0, n - 1, d);while(m -- ){int u, v;cin >> u >> v;if(pos.count(u) && pos.count(v)){int a = u, b = v;while(a != b){if(dep[a] > dep[b]) a = f[a];else b = f[b];}if(a != u && a != v) printf("LCA of %d and %d is %d.\n", u, v, a);else if(u == a) printf("%d is an ancestor of %d.\n", a, v);else printf("%d is an ancestor of %d.\n", a, u);}else if(pos.count(u) == 0 && pos.count(v) == 0)printf("ERROR: %d and %d are not found.\n", u, v);else if(pos.count(u) == 0)printf("ERROR: %d is not found.\n", u);else if(pos.count(v) == 0)printf("ERROR: %d is not found.\n", v);}return 0;} Harvest:
To build a binary tree, it is not necessary to build the tree completely. According to the required conditions, you can create f [ ] -> save the parent node of each node, or you can create l [ ] r[ ] -> save each nodeleft and right children.(The same applies to multi-fork trees)
边栏推荐
猜你喜欢
Wigner-Ville distribution for time-frequency analysis

2022-07-25 第六小组 瞒春 学习笔记

只出现一次的数字||| —— 哈希映射、异或位运算+分治思想
集成电路实践----D触发器

2022年安全员-A证考试试题及模拟考试
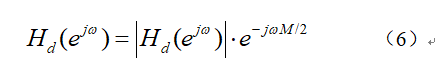
Window function method for FIR filter design
Servlet运行原理_API详解_请求响应构造进阶之路(Servlet_2)

MySQL 视图(详解)
【无标题】
2021 Huawei Cup Mathematical Modeling Contest E question - Ultra-Wideband (UWB) precise positioning problem under signal interference
随机推荐
PAT Class A 1145 Hash - Average Lookup Time
(数学基础)第三章-3.2-标准记号和常用函数
类加载过程
C语言的基本程序结构详细讲解
加载事件的用法
Selenium元素定位方法总结
MySQL (2)
2022年低压电工考试试题及在线模拟考试
集成电路实践----D触发器
DOM - Event Delegate
DOM - Event Mechanism and Event Chain
【无标题】
IPtables 和binlog
机械键盘失灵
XGBoost 和随机森林在表格数据上优于深度学习?
2022-07-09 第五小组 瞒春 学习笔记
A status code, and access baidu process
Based on the SVM regression forecast 】 【 LibSVM realize the prediction of a characteristic data
软件代码签名证书怎么申请
【无标题】