（数学基础）第三章-3.2-标准记号和常用函数

1、单调性

若 m <= n，有f(m) <= f(n)，那么f(n)单调递增。

若 m >= n，有f(m) >= f(n)，那么f(n)单调递减。

若 m < n，有f(m) < f(n)，那么f(n)严格递增。

若 m > n，有f(m) > f(n)，那么f(n)严格递减。

2、向下取整和向上取整

可以从字面意思理解，两者分别对应小于这个数的最大整数和大于这个数的最小整数

（1）对所有实数x

（2）对任意整数n

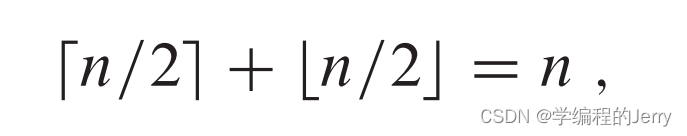
（3） 对任意实数x >= 0和整数a,b > 0

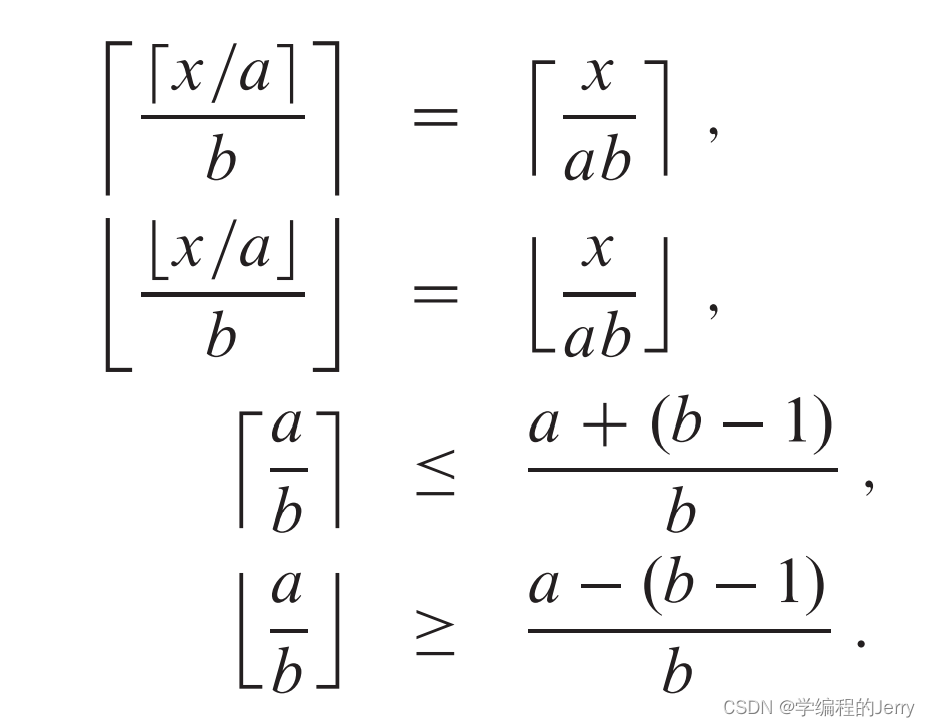
3、模运算

a mod n 就是a除以n所得的余数。

比如7 mod 5 = 2

4、多项式

n的d次多项式表达式为以下形式

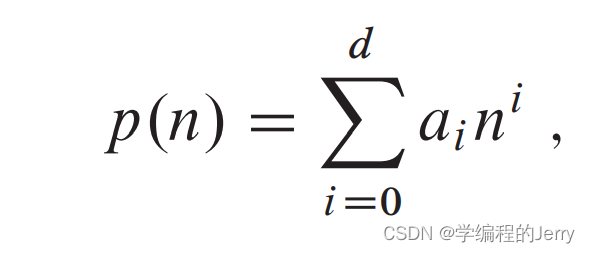
其中ai为系数，如果对某个常量k，有 

 那么称其为多项式有界。

5、指数

基本的不用多说，下面将多项式和指数相关联

（1）对于所有使得a>1的实常量a、b有

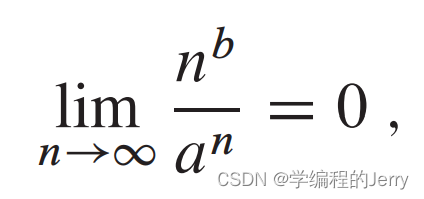
 由此可得：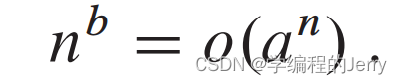 

 因此任意底大于1的指数函数比任意多项式指数函数增长得快

（2）使用e来做底数，有

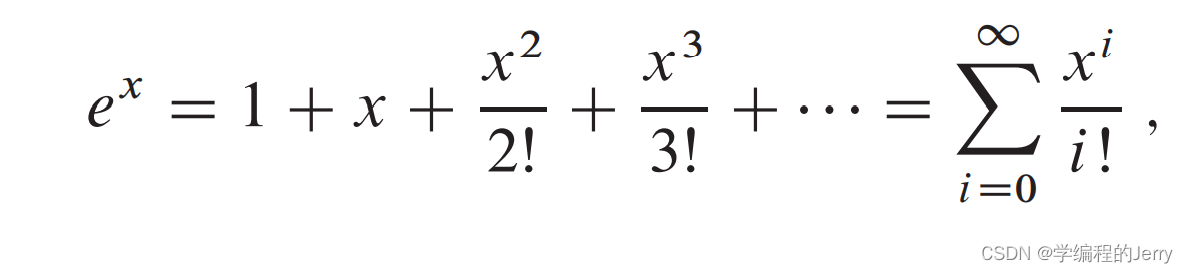
（3）对所有实数，有

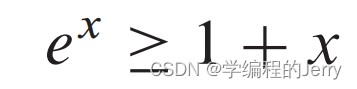
 当x=0等号成立

（4）当x的绝对值小于1的时候，近似估计

 （5）当x趋于0时

6、对数

（1）默认

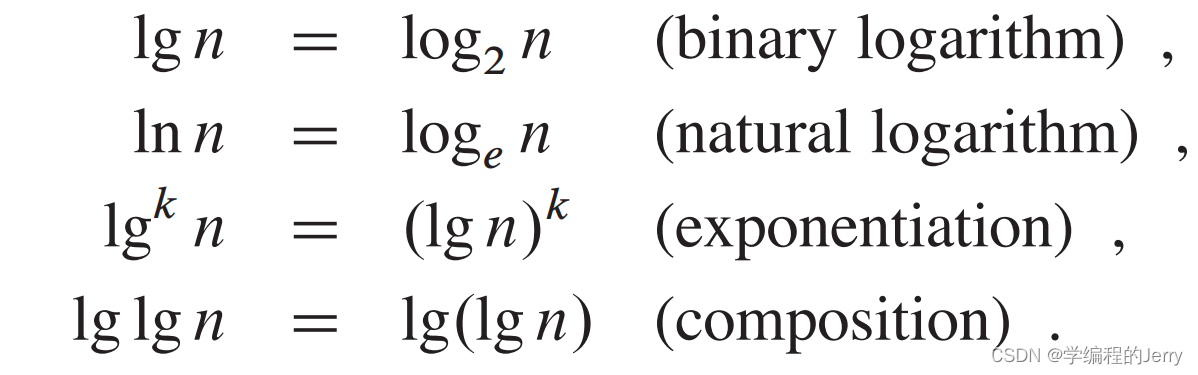
（2）对所有实数a\b\c>0，和n，有

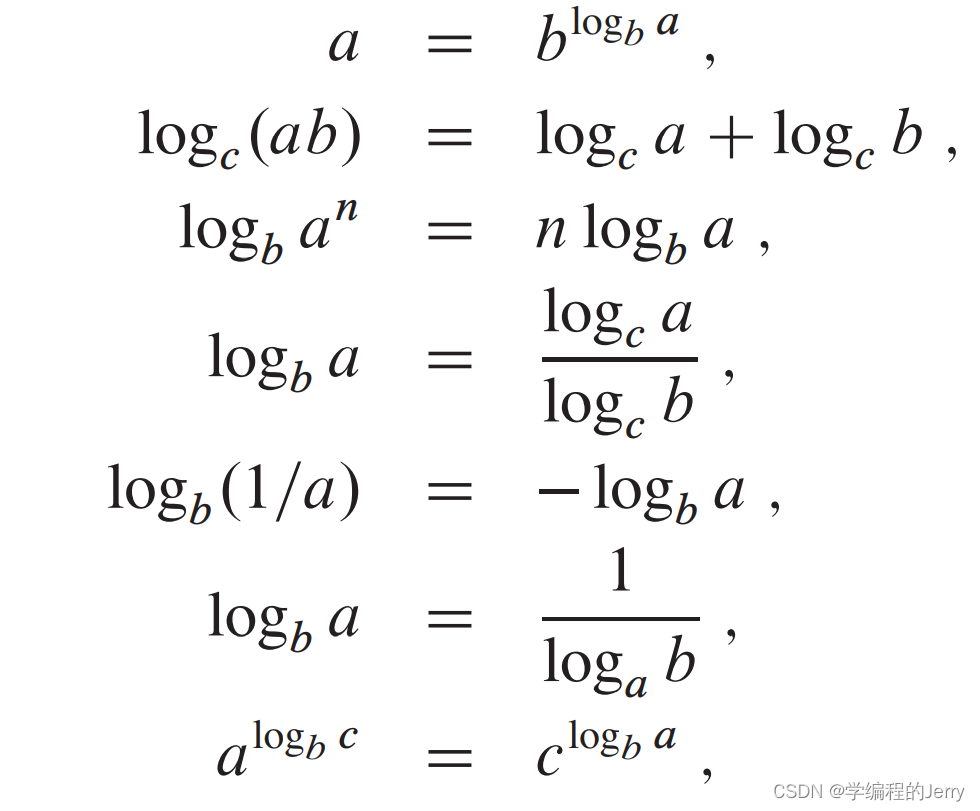
 （3）当x的绝对值小于1时，有以下级数展开

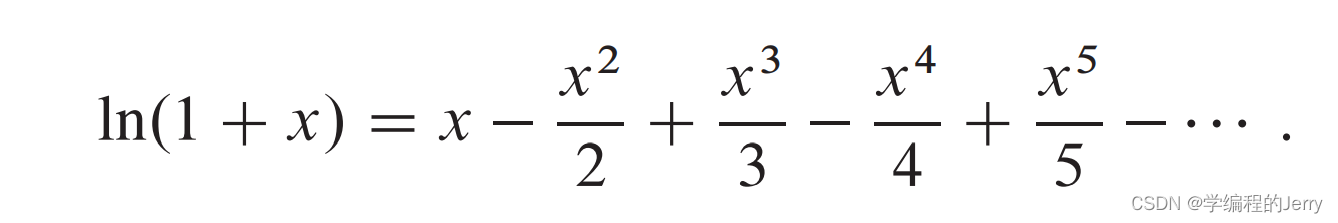
（4）对x > -1，有 

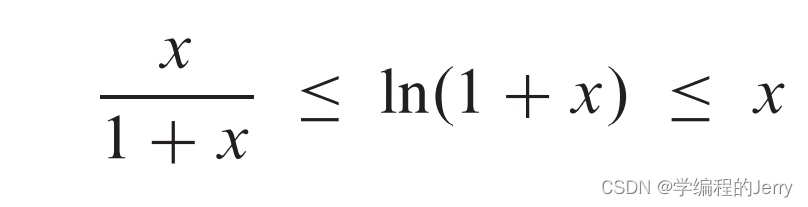
当x = 0时等号成立

（5） 对于某个常量k，有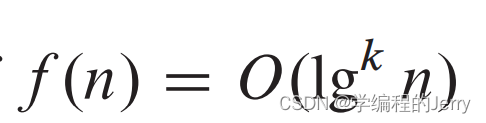

 则称函数f(n)多对数有界。

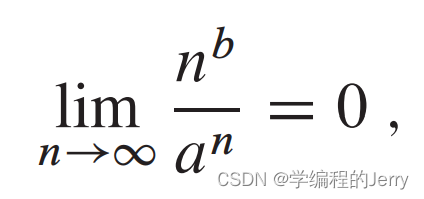
将lgn代替n，并用2的a次方代替a，可以让多项式和多对数增长互相关联

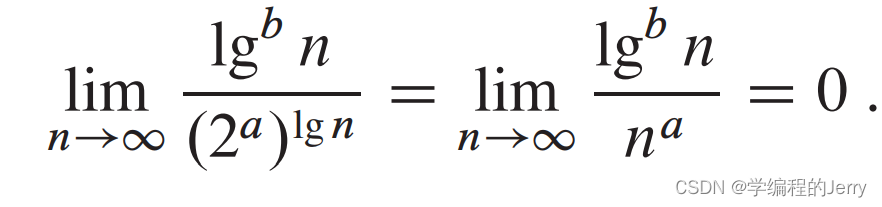
从而得到对于任意常量a>0，有

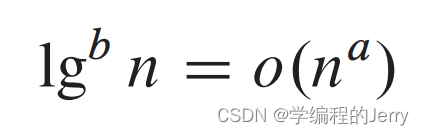
 7、阶乘

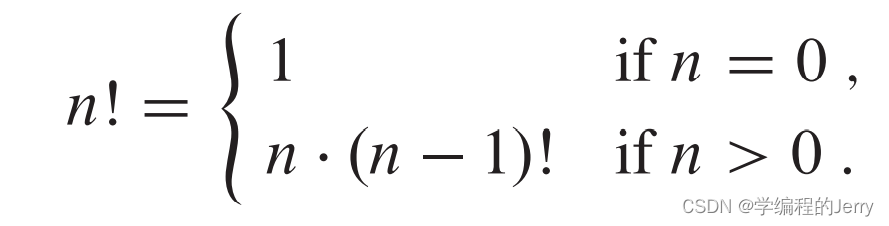
 补充：斯特林近似公式

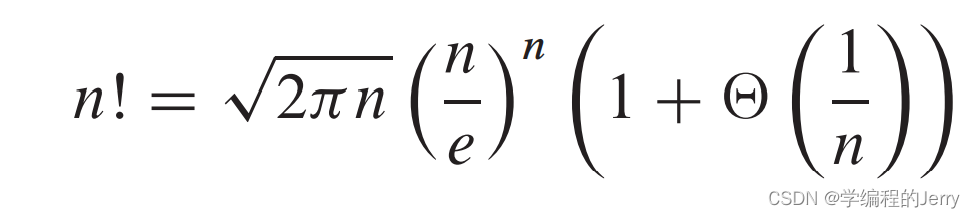
这一公式给出了更为紧确的上界和下界，下面等式也成立

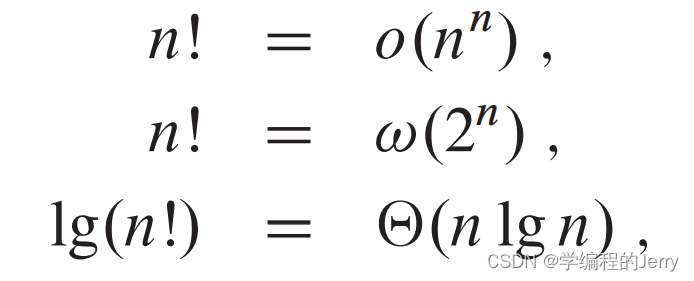
 对所有n>=1下面公式也成立

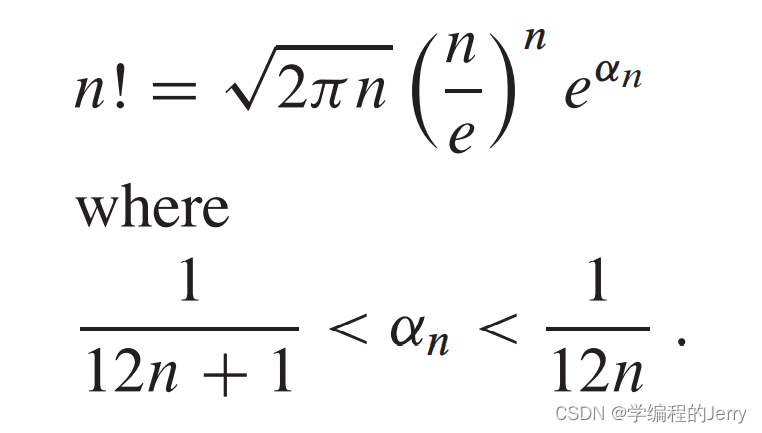
8、多重函数

对于非负整数i，我们递归定义：

举个例子：

 

9、多重对数函数

：从参数n开始，连续运用对数i次

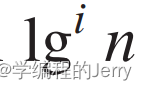 ：n的对数的i次幂

多重对数函数为:lg*n: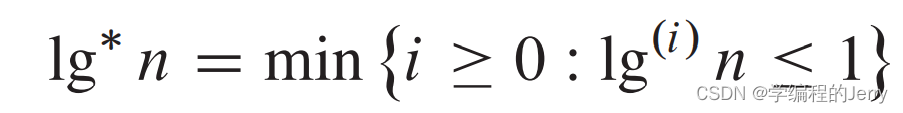

 例子：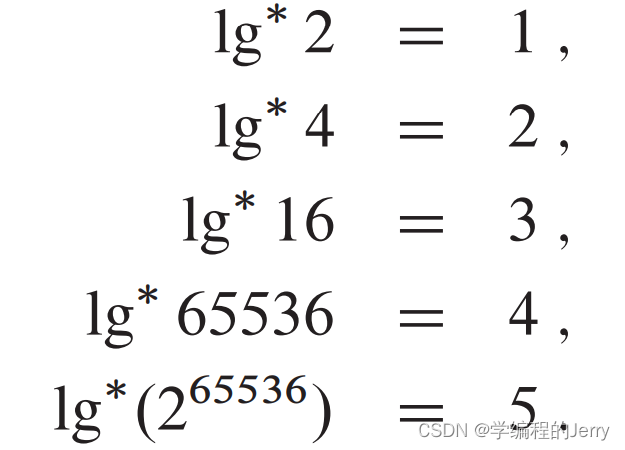

10、斐波那契数

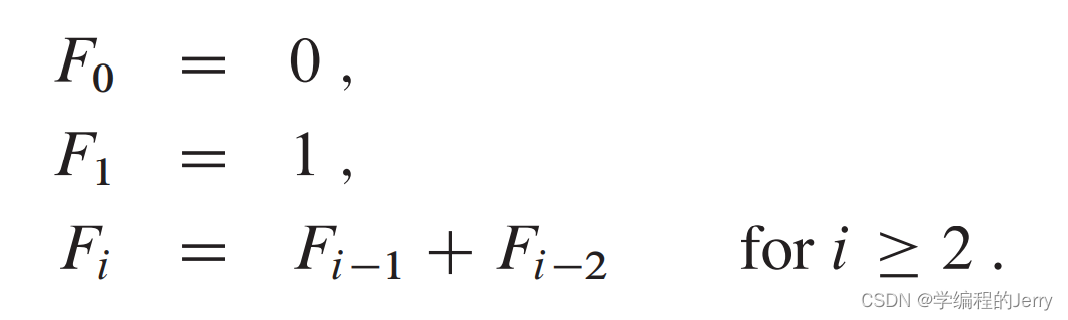
 斐波那契数是以指数形式增长的。