【Frequency Domain Analysis】Spectral leakage, frequency resolution, picket fence effect

一、时域加窗

Most signals are continuous in real life,Through the continuous signal sampling get scattered time signal,But the computer can handle data are limited long,So we can do it to the original sequence加窗处理Make it a finite length sequences.
In the case of rectangular window,其时域表达式为：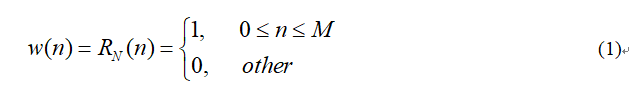
式(1)中,$N=M+1$,The length of the rectangular window.

Add a window on the infinite long sequence processing,Sequence is superior in the time domain to a window function.
By the convolution theorem can get,The time domain convolution of multiplication is equal to the frequency domain.

Set up the simulation signal of time domain expression for：
$$x(t)=A_0\ast cos(2\pi f_{0}t)+A_1\ast cos(2\pi f_{1}t)$$
$x(t)$做傅里叶变换（FT）的频域表达式为：
$$X(j\Omega )=A_0\pi \delta (\Omega +{\Omega }_0)+A_0\pi \delta (\Omega -{\Omega }_0)+A_1\pi \delta (\Omega +{\Omega }_0)+A_1\pi \delta (\Omega -{\Omega }_0)$$
连续信号$x(t)$The waveform and spectrum is shown in figure1所示.

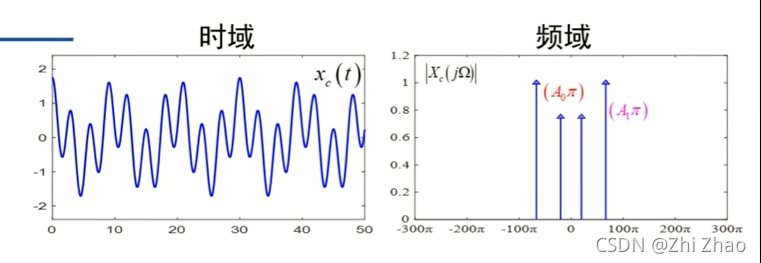
连续信号$x(t)$经过采样后,The discrete time expression is in the form of：
$$x[n]=x(t){|}_{t=n{T}_s}$$
离散序列$x[n]$For discrete time Fourier transform（DTFT）的频域表达式为：
$$X(e^{jw})=\frac{1}{T_s}\sum _{k=-\infty }^{\infty }X(j\frac{w}{T_s}-jk\frac{2\pi }{T_s})$$
离散序列$x[n]$The waveform and spectrum is shown in figure2所示.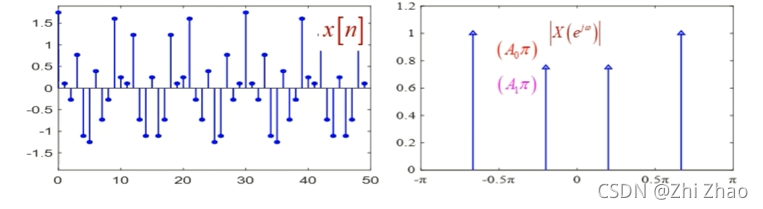

矩形窗函数$w[n]$For discrete time Fourier transform（DTFT）的频域表达式为：
$$W(e^{jw})=e^{-jw(N-1)/2}\ast \frac{sin(wN/2)}{sin(w/2)}$$

矩形窗函数$w[n]$The waveform and spectrum is shown in figure3所示.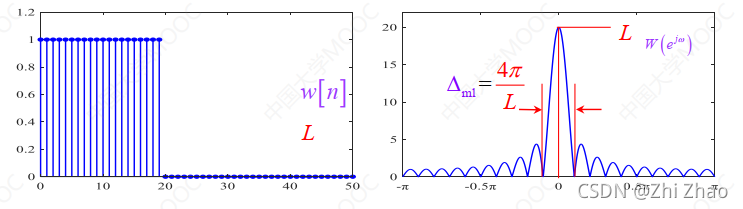

离散序列$x[n]$与窗函数$w[n]$的卷积为：
$$V(e^{jw})=\frac{1}{2\pi }{\int }_{-\pi }^{\pi }X(e^{j\theta })W(e^{j(w-\theta )})d\theta =\frac{A_0}{2}W(e^{j(w+w_0)})+\frac{A_0}{2}W(e^{j(w-w_0)})+\frac{A_1}{2}W(e^{j(w+w_0)})+\frac{A_1}{2}W(e^{j(w-w_0)})$$
After the truncation of discrete sequence$v[n]$The waveform and spectrum is shown in figure4所示.

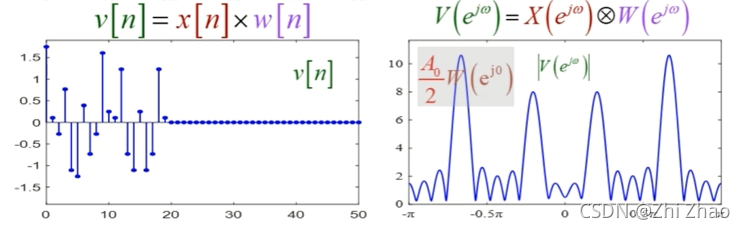
频谱泄露

The frequency of the signal components include1MHz和1.05MHz,1MHzThe corresponding amplitudes as1,但是1.05MHzAmplitude reduced,And the other has no small amplitude frequency point.This is the emergence of the phenomenon of frequency spectrum leakage.

Causes of spectrum leakage is what？

Due to the limited computer can only handle long data,So need to sampled signal is truncated,Equivalent to the original signal did add window processing.To add window is superior to signal in time domain signal by a window function,Time the product of the corresponding frequency domain convolution,The window function in the frequency domain including the main lobe and side lobe,Sidelobe caused the signal frequency spectrum leakage.Frequency domain leakage is inevitable,只能减小.

How to restrain the phenomenon？

Can take longer data points,The closer to the original data, the better,But the downside is that the computation increase;
Can choose spectral energy of side lobe smaller window function.
The typical window function,The frequency of the rectangular window highest resolution,Maximum sidelobe leak.

二、频率分辨率

How to calculate the frequency resolution？

In order to facilitate understanding what is the frequency resolution,The frequency resolution can be divided into two types,A waveform frequency resolution is（Waveform Frequency Resolution,Shorthand for waveform resolution）,Also known as visual frequency resolution,另一种则为FFT频率分辨率（简记为FFT分辨率）.

Waveform resolution：在频谱图中,The smallest interval of two frequency resolution can be,Associated with the length of original signal.
$$△R_w=\frac{1}{T}$$
其中,$T$For the length of the original data.

FFT分辨率：In the spectrum image data points,With the signalFFTCalculation of points about.
$$△R_{fft}=\frac{F_s}{N_{fft}}$$
其中,$F_s$为采样频率,$N_{fft}$For the signalFFTWhen calculating the points.

How to improve the frequency resolution？

例如,A composite signal time domain expression for$x(t)=cos(2\pi f_{1}t)+cos(2\pi f_{2}t)$
其中$f_1=1MHz$,$f_2=1.05MHz$.$x(t)$The waveform and spectrum is shown in figure6所示.

By the above spectrum can be found in the,在1MHzNear the two frequency aliasing,无法有效区分1MHz和1.05MHz,Shows the frequency resolution is not enough.

The time domain data are zero padding,Can change the frequency resolution？For example, in the original data points behind add6000个数值为0的点,Has no effect on the signal itself data,Just increased participation inFFTThe calculation of data points,Get the signal waveform and spectrum is shown in figure7所示.

Based on the original data for补零操作,Data points in the spectrum image more intensive.But I still can't distinguish between1MHz和1.05MHz,Prove that the signal waveform frequency resolution and participate inFFTThe calculation of data points$N_{fft}$无关,Only with the length of the original data$T$有关.Zero padding on the time-domain equivalent to the frequency domain interpolation on,The increased frequency points,The spectrum curve becomes more smooth,即增加了FFT频率分辨率.

为了有效区分1MHz和1.05MHz,Must extend the length of the original data in order to improve the waveform resolution.At the same sampling frequency of the original signal sampling,采集7000个数据点.Get the signal waveform and spectrum is shown in figure8所示.

有图8可见,1MHz和1.05MHzCan be separate,But also appeared a phenomenon of frequency spectrum leakage.The signal waveform resolution of at this time：$△R_w=\frac{1}{70us}\approx 14KHz$,小于1MHz和1.05MHz之间的距离$50KHz$.

In order to reduce spectral leakage,The original signal take longer data points,采集8000个数据点.Get the signal waveform and spectrum is shown in figure9所示.

由图9可知,1MHz和1.05MHzThe corresponding amplitudes are1,And can effectively distinguish,The signal at this timeFFT分辨率为：$△R_{fft}=\frac{F_s}{8000}=12.5KHz$,刚好是1MHz和1.05MHz的公约数,即$1MHz=12.5KHz\times 80$,$1.05MHz=12.5KHz\times 84$.
So take the proper length of data points can reduce the spectrum leakage.

三、频域采样

周期序列的DFS的系数$X(k)$与$x(n)$A cycle of$Z$Transformation in the unit circle$N$A uniform point sampling values are equal,This is the frequency domain sampling.

频域采样定理：
当$N\ge L$,即DFTCalculate the length of the points will be greater than or equal to the signal in frequency domain sampling,Frequency domain sampling will not result in time domain aliasing.
有限长序列$x(n)$的$Z$变换为：
$$X(Z)=\sum _{n=0}^{N-1}x(n)Z^{-n}=\sum _{n=0}^{N-1}[\frac{1}{N}\sum _{k=0}^{N-1}X(k)W_N^{-kn}]Z^{-n}=\frac{1-Z^{-N}}{N}\sum _{k=0}^{N-1}\frac{X(k)}{1-W_N^{-k}{Z}^{-1}}$$
其中,$W_N^{-kn}=e^{j\frac{2\pi kn}{N}}$,$W_N^{-k}=e^{j\frac{2\pi k}{N}}$.

栅栏效应

在进行DFTCalculations need frequency domain of signal sampling,Due to the sampling interval as$△w=\frac{2\pi }{N}$,The spectrum diagrams are composed of discrete spectral lines of a root,Like watch on location through the fence.

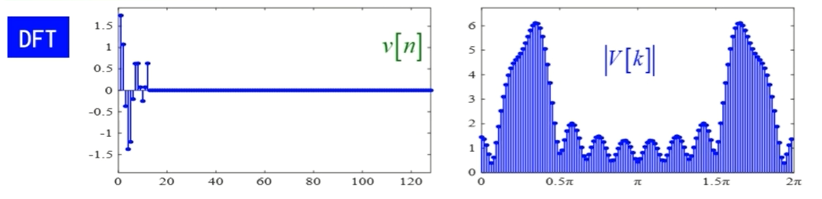
How to alleviate the fence effect？

The increase in frequency domain sampling pointsN（Don't change the time domain data under the condition of,在时域数据末端添加一些零值点,使得谱线更密）,Narrow spectral line spacing,Reduce the fence effect.

四、MATLAB代码

%% 1000Data points of the waveform and spectrum
clc;
clear;
close all;

Fs = 100e6;             % 采样频率
f1 = 1e6;f2 = 1.05e6;   % 信号的频率
T = 1/Fs;               % 采样周期
L0 = 1000;              % 信号长度
L = 1000;               % 数据长度
t0 = (0:L0-1)*T;        % Signal time series
t = (0:L-1)*T;          % The data time series
x = cos(2*pi*f1*t0)+cos(2*pi*f2*t0);  % 原始信号

% FFT
[f1,A1] = PinPu(x,Fs);
figure(1)
subplot(1,2,1);plot(t*1e6,x);
xlabel('t/us');title('时域');
subplot(1,2,2);plot(f1,A1);
xlabel('f/Hz');title('频域');xlim([0 2e6]);

%% The spectrum leakage phenomena
clc;
clear;
close all;

Fs = 100e6;             % 采样频率
f1 = 1e6;f2 = 1.05e6;   % 信号的频率
T = 1/Fs;               % 采样周期
L0 = 7000;              % 信号长度
L = 7000;               % 数据长度
t0 = (0:L0-1)*T;        % Signal time series
t = (0:L-1)*T;          % The data time series
x = cos(2*pi*f1*t0)+cos(2*pi*f2*t0);  % 原始信号
% FFT
[f1,A1] = PinPu(x,Fs);
figure(1)
subplot(1,2,1);plot(t*1e6,x);
xlabel('t/us');title('时域');
subplot(1,2,2);plot(f1,A1);
xlabel('f/Hz');title('频域');xlim([0 2e6]);

%% 8000Data points of the waveform and spectrum,Enhance the frequency resolution.
clc;
clear;
close all;

Fs = 100e6;             % 采样频率
f1 = 1e6;f2 = 1.05e6;   % 信号的频率
T = 1/Fs;               % 采样周期
L0 = 8000;              % 信号长度
L = 8000;               % 数据长度
t0 = (0:L0-1)*T;        % Signal time series
t = (0:L-1)*T;          % The data time series
x = cos(2*pi*f1*t0)+cos(2*pi*f2*t0);  % 原始信号
% FFT
[f1,A1] = PinPu(x,Fs);
figure(1)
subplot(1,2,1);plot(t*1e6,x);
xlabel('t/us');title('时域');
subplot(1,2,2);plot(f1,A1);
xlabel('f/Hz');title('频域');xlim([0 2e6]);

参考文献

[1] 数字信号处理
[2] Fourier transform of the frequency and waveform resolution
[3] 补零、频谱泄露、Fence effect relationship？