第四章-4.1-最大子数组问题

一、背景引入

你获得了投资一家公司的机会，这家公司的股票并不是很稳定；你被准许在某一天买进股票，并且在之后某一天将其卖出，买进和卖出都是在当天交易结束以后进行；你可以了解股票未来的价格，目标是获得最大化的收益。

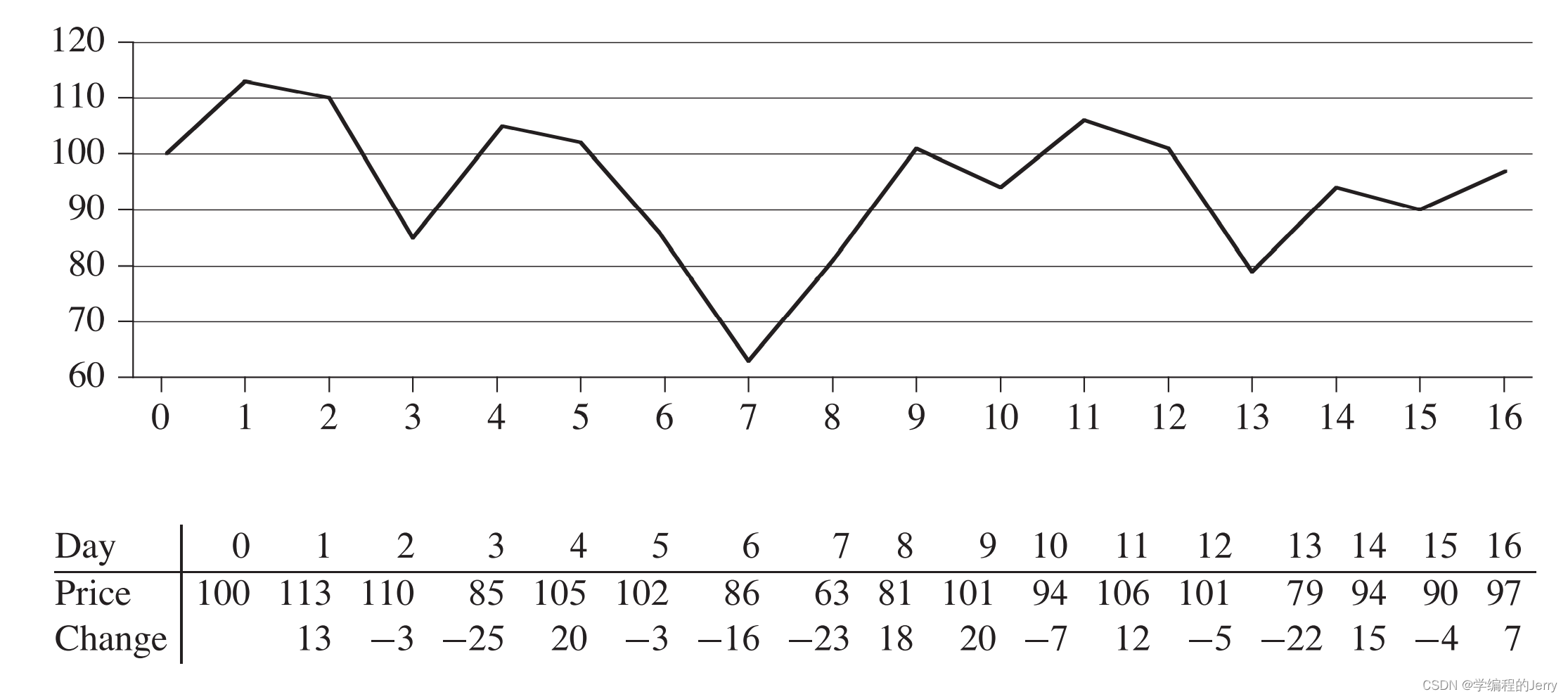
 图1

上图为其股票价格变化信息，横轴为日期，纵轴为价格，表格的最后一行给出了股票价格相对前一天的变化。

二、尝试探索

我们或许想要在最低价买入，最高价卖出，但是图中最高价是第1天，最低价是第7天，因此我们这个策略是失败的。下图的案例同样可以说明这个道理

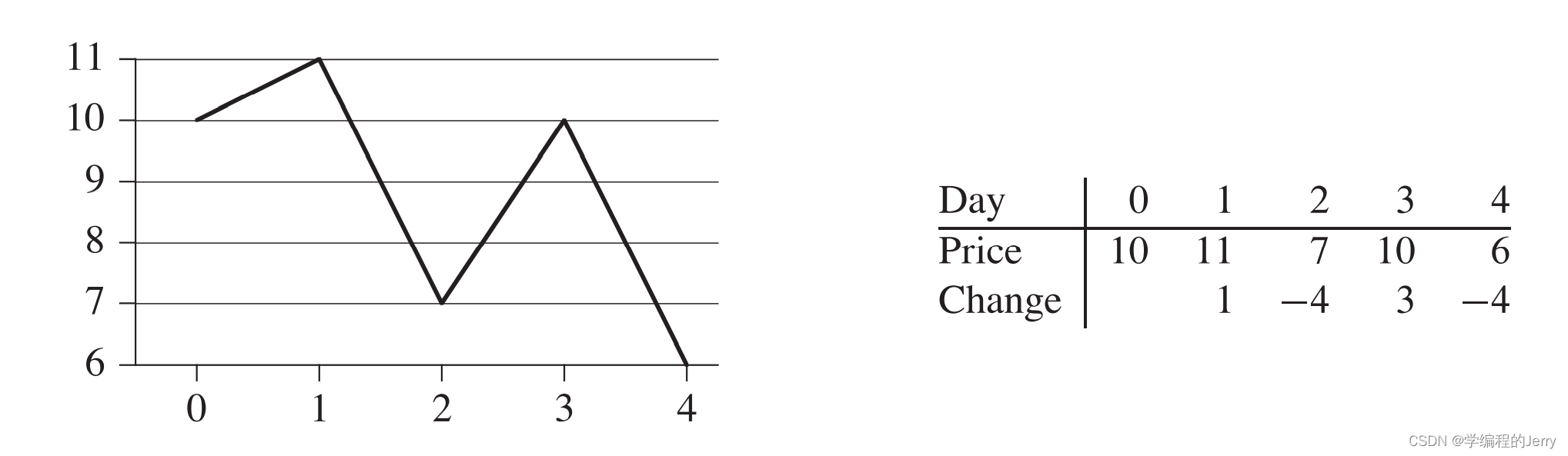
图2

我们可以发现，上图中第2天买进，第3天卖出可以给我们带来最大的收益，很明显他们既不是最低价也不是最高价。

三、不同的方法

（1）暴力求解方法

tip：只需要尝试每对可能的买进和卖出的日期组合，满足卖出时间在买入之后即可。

（1）那么我们可以使用组合的方法，得到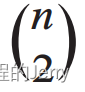，即Cn(2)（组合符号有点难打）

（2）加上处理每对日期所花费的时间也是常量。

因此这个算法的运行时间是Ω(n²)，即其下界（最少）也要这个时间。

（2）换一种思路（采用分治策略）

【1】最大子数组是什么？

观察图1中最后一行，我们可以转换思路，找到一段日期，让这一段日期的第一天和最后一天之间的股票增值最大（通过求这一段所有数字的和），我们称这一段为最大子数组。

例如图1最后一行的最大子数组就是下图，可得最大收益为43美元。

【2】使用分治策略

a、要寻找子数组A[low...high]中的最大子数组，我们使用分治技术，将子数组划分成两个规模同等的子数组。先找到子数组的中央位置mid，考虑求解两个子数组A[low...mid]和A[mid...high]。最大子数组A[i...j]必定在其中有三种情况。

• 完全位于A[low...mid]中，此时low <= i <= j <= mid。
• 完全位于A[mid...high]中，此时mid < i <= j <= high。
• 跨越中点，low <= i <= mid < j <= high。

如图所示

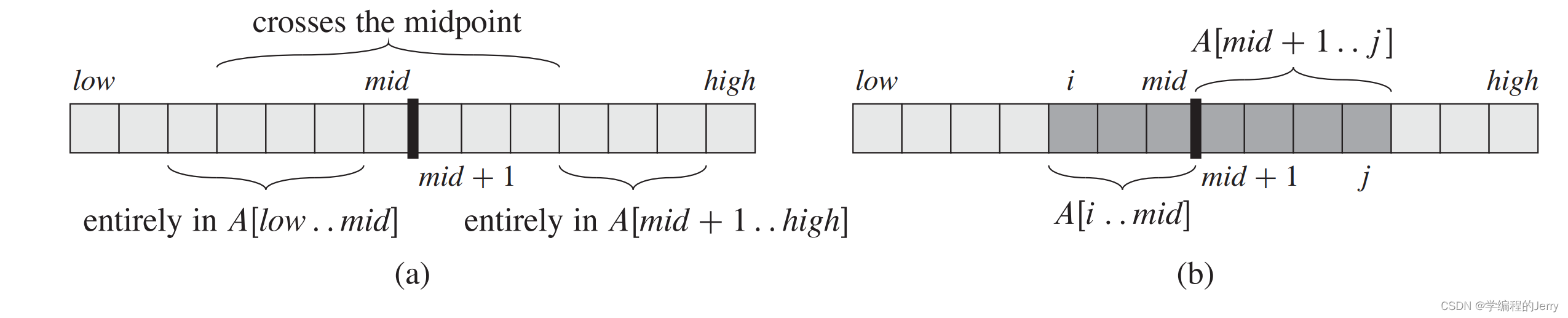
【3】如何求三种情况

①完全位于A[low...mid]中：依旧是最大子数组问题，递归即可完成（将其看成母数组）

②完全位于A[mid...high]中：同①

③跨越中点：从mid向左和向右遍历，分别找到和最大的左右两个子数组（必须是mid往左往右的延伸）

我们只需要求③，因为①②仅仅需要递归就可完成，下面给出伪代码：

FIND-MAX-CROSSING-SUBARRAY(A,low,mid,high)
1  left-sum = -∞                //寻找左边边界i和左边最大值left-sum
2  sum = 0
3  for i = mid downto low
4      sum = sum + A[i]
5      if sum > left-sum        //如果sum大于left-sum时，记录新的sum值与此时边界的下标
6          left-sum = sum
7          max-left = i
8  right-sum = -∞
9  sum = 0
10 for j = mid + 1 to high      //寻找右边边界j和右边最大值right-sum
11     sum = sum + A[j]
12     if sum > right-sum
13         right-sum = sum
14         max-right = j
15 return(max-left,max-right,left-sum + right-sum)    //返回左右边界i和j与最大子数组总和

【4】调用FIND-MAX-CROSSING-SUBARRAY的运行时间

①两个for循环每次花费Θ(1)的时间，只需要算一共执行了多少次迭代

②3~7行for循环执行了mid - low + 1次迭代

③10~14行for循环执行了high - mid次迭代

总循环次数为 mid - low + 1 + high - mid = high - low + 1 = n

因此运行时间为Θ(n)

【5】综合情况（以FIND-MAX-CROSSING-SUBARRAY为基础构建整个解决问题的伪代码）

FIND-MAXIMUM-SUBARRAY(A,low,high)
1 if high == low                        //在递归过程中，high=low的时候为转折点
2     return(low,high,A[low])

3 else mid = ⌊(low + high) / 2 ⌋
    //通过递归求出left-sum和right-sum以及各自的边界
4     (left-low,left-high,left-sum) = 
            FIND-MAXIMUM-SUBARRAY(A,low,mid)
5     (right-low,right-high,right-sum) = 
            FIND-MAXIMUM-SUBARRAY(A,mid+1,high)

    //调用FIND-MAX-CROSSING-SUBARRAY()求出cross-sum以及边界
6     (cross-low,cross-high,cross-sum) = 
            FIND-MAX-CROSSING-SUBARRAY(A,low,mid,high)

    //三者互相比较，找出和最大的（子数组）
7     if left-sum >= right-sum and left-sum >= cross-sum
8           return(left-low,left-high,left-sum)
9     elseif right-sum >= left-sum and right-sum >= cross-sum
10          return(right-low,right-high,right-sum)
11    else return(cross-low,cross-high,cross-sum)

【6】关于递归（对递归没有疑惑的可以跳过）

 这是我手写的其中一部分过程，在求left-sum时的递归，我把调用函数的顺序和所在伪代码第几行标在了图上，大家可以参考

【7】C++代码实现

大家可以靠此代码调试

#include <iostream>
using namespace std;
const int Infinite = -10000;

int FindMaxCrossSubarray(int A[], int low, int mid, int high)  //跨越中点的数组
{
	cout << "调用FindMaxCrossSubarray" << endl;
	int left_sum = Infinite;
	int sum = 0;
	for (int i = mid; i >= low; i--)  //左半部的最大子数组
	{
		sum += A[i];
		if (sum > left_sum)
		{
			left_sum = sum;
			//max_left = i;
		}
	}

	int right_sum = Infinite;
	sum = 0;
	for (int i = mid + 1; i <= high; i++)  //右半部的最大子数组
	{
		sum += A[i];
		if (sum > right_sum)
		{
			right_sum = sum;
			//max_right = i;
		}
	}
	return left_sum + right_sum;
}

int FindMaxSubarray(int A[], int low, int high)
{
	cout << "调用FindMaxSubarray" << endl;
	int left_sum, right_sum, cross_sum;
	if (high == low)
	{
		return A[low];
	}
	else
	{
		int mid = (low + high) / 2; //分治
		left_sum = FindMaxSubarray(A, low, mid);  //前半部
		right_sum = FindMaxSubarray(A, mid + 1, high);  //后半部
		cross_sum = FindMaxCrossSubarray(A, low, mid, high);  //跨越前后

		if (left_sum >= right_sum && left_sum >= cross_sum) {
			//最大子数组在左边
			cout << "返回left_sum" << endl;
			cout << left_sum << endl;
			return left_sum;

		}
		else if (right_sum >= left_sum && right_sum >= cross_sum) {
			//最大的数组在右边
			cout << "返回right_sum" << endl;
			cout << right_sum << endl;
			return right_sum;
		}
		else {
			//跨越
			cout << "返回cross_sum" << endl;
			cout << cross_sum << endl;
			return cross_sum;
		}
	}
}

int main()
{
	int a[] = { 13, -3, -25,20 , -3, -16, -23, 18, 20, -7, 12, -5, -22, 15, -4, 7 };
	int length = sizeof(a) / sizeof(int);

	cout << FindMaxSubarray(a, 0, length - 1) << endl;
	return 0;
}

【8】总运行时间分析

①n = 1，T(1) = Θ(1)

②n > 1时，第1、3行花费常量时间，是Θ(1)，4、5行是递归，递归中left和right问题规模都为n/2个元素（假设原问题规模为2的幂），这使总时间增加2T(n/2)。

③第6行已经求解过，FIND-MAX-CROSSING-SUBARRAY()的运行时间为Θ(n)

④7~11行也是常量时间Θ(1)

我们可以得到其递归式

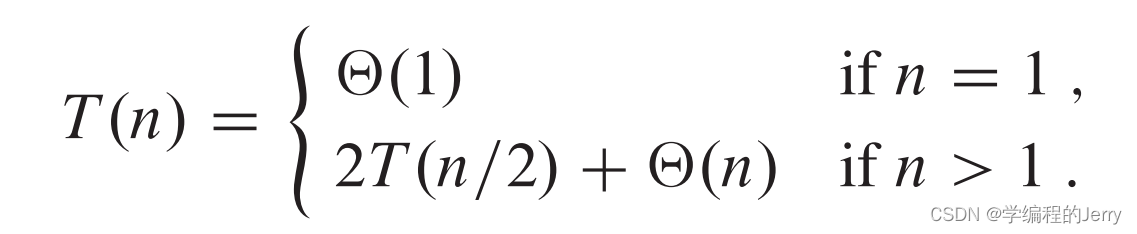
解是

这个答案的来源第二章已经讲过了，是有关递归树的知识，这里不再赘述。