当前位置:网站首页>E - Distance Sequence (前缀和优化dp
E - Distance Sequence (前缀和优化dp
2022-08-05 00:08:00 【__Rain】
E - Distance Sequence
思路:
d p [ i ] [ j ] dp[i][j] dp[i][j] 表示考虑前 i i i 个数,最后一个数为 j j j 时的方案数
显然 d p [ i ] [ j ] + = d p [ i − 1 ] [ l ] dp[i][j]+=dp[i-1][l] dp[i][j]+=dp[i−1][l], l l l 为前 i − 1 i-1 i−1 个数中以 l l l 结尾并且与 j j j 相接合法的情况
j − l ≥ k j-l\geq k j−l≥k,即 1 ≤ l ≤ j − k 1\leq l \leq j-k 1≤l≤j−k
l − j ≥ k l-j\geq k l−j≥k,即 j + k ≤ l ≤ m j+k \leq l \leq m j+k≤l≤m
显然可以维护一个前缀和优化
(注意需要特判 K = 0 K=0 K=0 的情况
code:
#include<bits/stdc++.h>
#define endl '\n'
#define ll long long
#define ull unsigned long long
#define ld long double
#define all(x) x.begin(), x.end()
#define mem(x, d) memset(x, d, sizeof(x))
#define eps 1e-6
using namespace std;
const int maxn = 2e6 + 9;
const int mod = 998244353;
const int inf = 0x3f3f3f3f;
const ll INF = 0x3f3f3f3f3f3f3f3f;
ll n, m;
ll dp[1009][5009];
void work()
{
int k;
cin >> n >> m >> k;
if(k == 0){
ll ans = 1;
for(int i = 1; i <= n; ++i)
ans = ans * m % mod;
cout << ans;
return;
}
vector <ll> sum(m + 1, 0);
for(int i = 1; i <= m; ++i) {
dp[1][i] = 1;
sum[i] = sum[i-1] + dp[1][i];
}
for(int i = 2; i <= n; ++i){
vector <ll> now_sum(m + 1, 0);
for(int j = 1; j <= m; ++j){
if(j - k >= 1)
(dp[i][j] += sum[j - k]) %= mod;
//for(int l = 1; l <= j - k; ++l)
// (dp[i][j] += dp[i-1][l]) %= mod;
if(j + k <= m)
(dp[i][j] += (sum[m] - sum[j+k-1] + mod) % mod) %= mod;
//for(int l = j + k; l <= m; ++l)
// (dp[i][j] += dp[i-1][l]) %= mod;
}
for(int j = 1; j <= m; ++j) now_sum[j] = (now_sum[j-1] + dp[i][j]) % mod;
sum = now_sum;
}
cout << sum[m];
}
int main()
{
ios::sync_with_stdio(0);
// int TT;cin>>TT;while(TT--)
work();
return 0;
}
改进 d p dp dp 过程就可以不用单独特判了,但是也要想到 k = = 0 k==0 k==0 的时情况,然后修改转移方程
code:
#include<bits/stdc++.h>
#define endl '\n'
#define ll long long
#define ull unsigned long long
#define ld long double
#define all(x) x.begin(), x.end()
#define mem(x, d) memset(x, d, sizeof(x))
#define eps 1e-6
using namespace std;
const int maxn = 2e6 + 9;
const int mod = 998244353;
const int inf = 0x3f3f3f3f;
const ll INF = 0x3f3f3f3f3f3f3f3f;
ll n, m, k;
ll dp[1009][5009];
void work()
{
cin >> n >> m >> k;
vector <ll> sum(m + 1, 0);
for(int i = 1; i <= m; ++i) {
dp[1][i] = 1;
sum[i] = sum[i-1] + dp[1][i];
}
for(int i = 2; i <= n; ++i){
vector <ll> now_sum(m + 1, 0);
for(int j = 1; j <= m; ++j){
int l = max(1ll, j - k + 1), r = min(m, j + k - 1);
if(k){
dp[i][j] = (sum[m] - (sum[r] - sum[l-1]) + mod) % mod;
}
else {
dp[i][j] = sum[m];
}
}
for(int j = 1; j <= m; ++j) now_sum[j] = (now_sum[j-1] + dp[i][j]) % mod;
sum = now_sum;
}
cout << sum[m];
}
int main()
{
ios::sync_with_stdio(0);
// int TT;cin>>TT;while(TT--)
work();
return 0;
}
想到 k = 0 k=0 k=0 时再改变转移方程,对于我这种菜鸡根本做不到啊,于是就出现了下边的写法,就可以完全不用考虑 K K K 的值了,只需要保证每次转移都合法即可(也就是 r > = l − 1 r>=l-1 r>=l−1)
code:
#include<bits/stdc++.h>
#define endl '\n'
#define ll long long
#define ull unsigned long long
#define ld long double
#define all(x) x.begin(), x.end()
#define mem(x, d) memset(x, d, sizeof(x))
#define eps 1e-6
using namespace std;
const int maxn = 2e6 + 9;
const int mod = 998244353;
const int inf = 0x3f3f3f3f;
const ll INF = 0x3f3f3f3f3f3f3f3f;
ll n, m, k;
ll dp[1009][5009];
// 考虑前i个数,最后一个数为j
void work()
{
cin >> n >> m >> k;
vector <ll> sum(m + 1, 0);
for(int i = 1; i <= m; ++i) {
// 单独一个数1-m都可以
dp[1][i] = 1;
sum[i] = sum[i-1] + dp[1][i];
}
for(int i = 2; i <= n; ++i){
vector <ll> now_sum(m + 1, 0);
for(int j = 1; j <= m; ++j){
int l = max(1ll, j - k + 1), r = min(m, j + k - 1);// 不合法的区间
dp[i][j] = sum[m];
if(r >= l - 1) {
// 不合法区间存在就需要删
dp[i][j] = (dp[i][j] - (sum[r] - sum[l-1]) + mod) % mod;
}
}
for(int j = 1; j <= m; ++j) now_sum[j] = (now_sum[j-1] + dp[i][j]) % mod;
sum = now_sum;
}
cout << sum[m];
}
int main()
{
ios::sync_with_stdio(0);
// int TT;cin>>TT;while(TT--)
work();
return 0;
}
边栏推荐
猜你喜欢

uniapp横向选项卡(水平滚动导航栏)效果demo(整理)
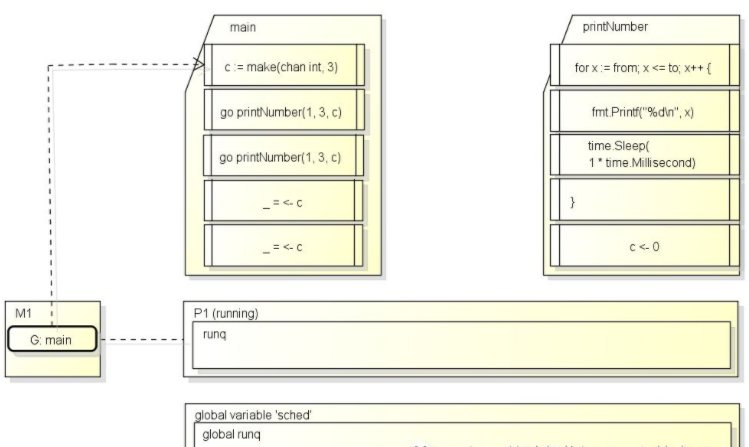
Implementation principle of golang coroutine
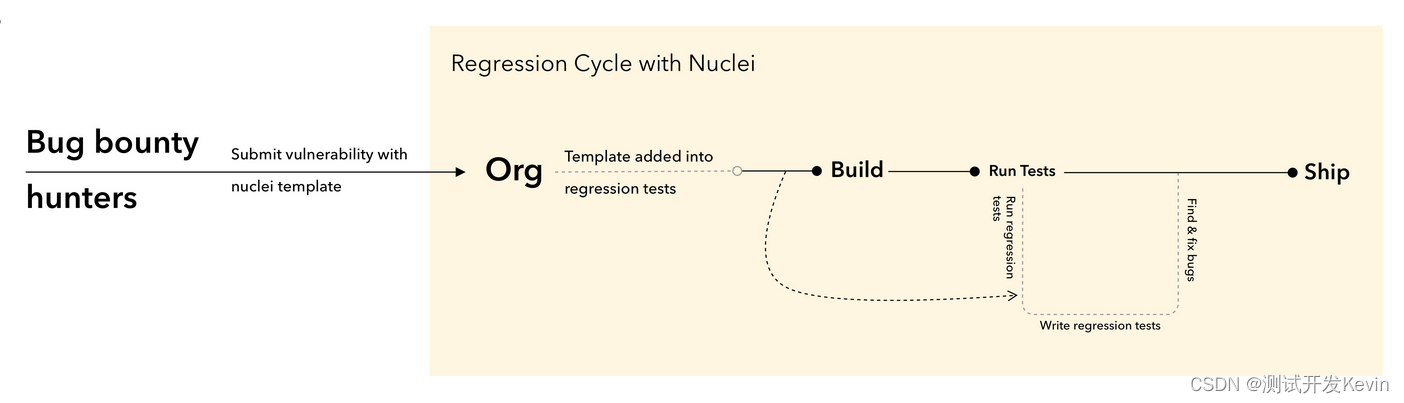
Nuclei (2) Advanced - In-depth understanding of workflows, Matchers and Extractors

安全软件 Avast 与赛门铁克诺顿 NortonLifeLock 合并案获英国批准,市值暴涨 43%

如何写好测试用例

测试经理要不要做测试执行?
Xiaohei's leetcode journey: 95. Longest substring with at least K repeating characters
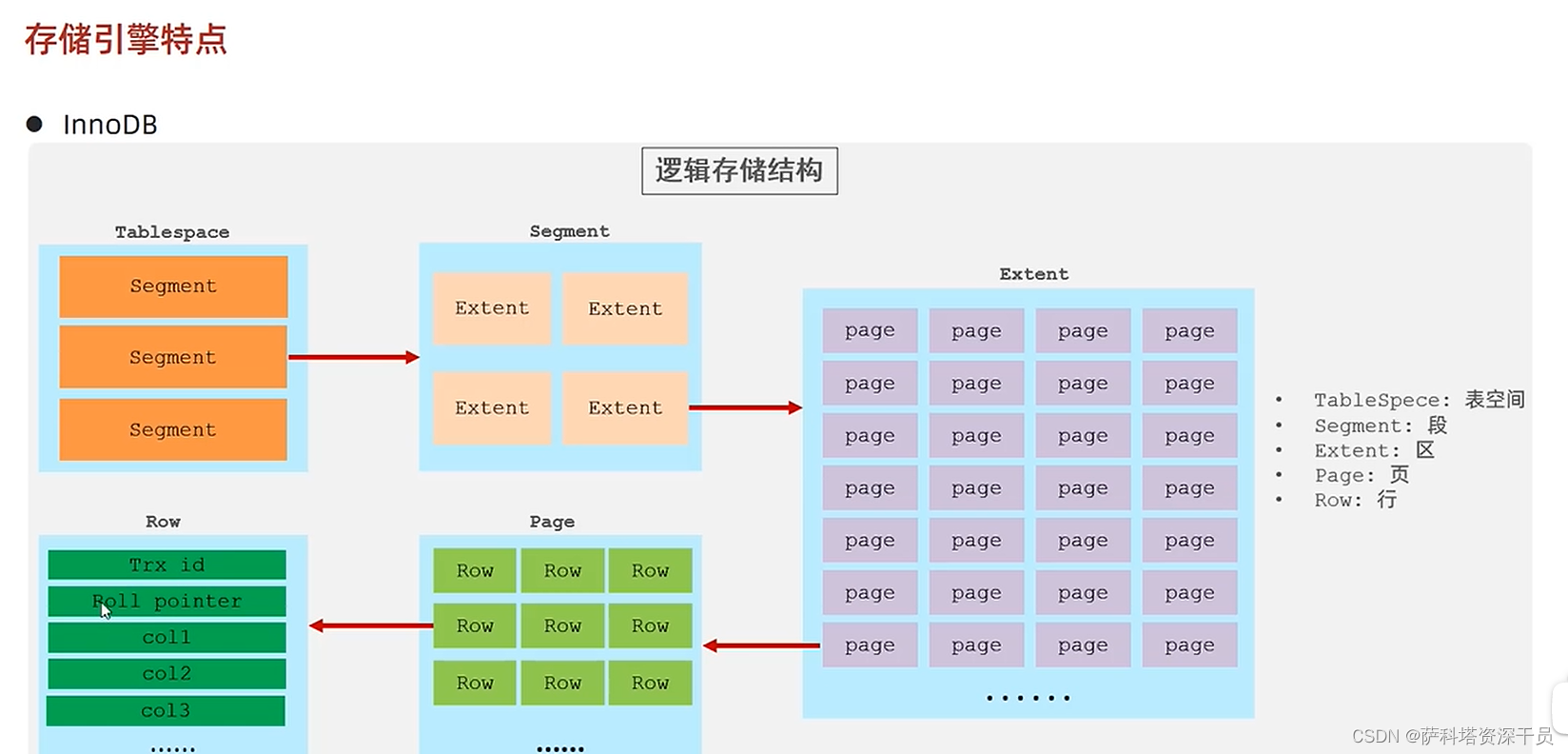
Mysql_14 存储引擎
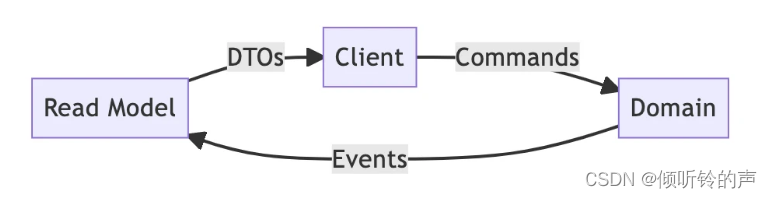
从单体架构迁移到 CQRS 后,我觉得 DDD 并不可怕
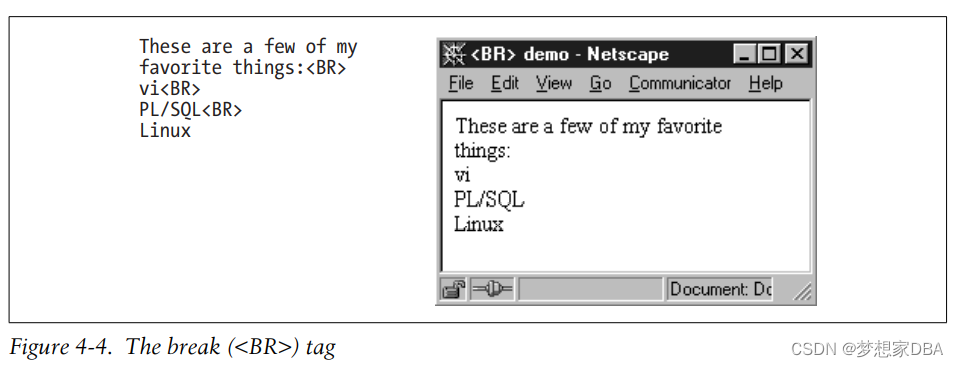
Basic web in PLSQL
随机推荐
【云原生--Kubernetes】Pod控制器
RK3399平台开发系列讲解(内核调试篇)2.50、嵌入式产品启动速度优化
论文解读( AF-GCL)《Augmentation-Free Graph Contrastive Learning with Performance Guarantee》
4 - "PyTorch Deep Learning Practice" - Backpropagation
KT6368A Bluetooth certification problem_FCC and BQB_CE_KC certification or other instructions
网站最终产品页使用单一入口还是多入口?
工业物联网 —— 新型数据库的召唤
头脑风暴:完全背包
Mysql_14 存储引擎
MAUI Blazor 权限经验分享 (定位,使用相机)
Basic web in PLSQL
uniapp 分享功能-分享给朋友群聊朋友圈效果(整理)
Senior game modelers tell newbies, what are the necessary software for game scene modelers?
Cython
00、数组及字符串常用的 API(详细剖析)
【LeetCode】图解 904. 水果成篮
仿网易云音乐小程序-uniapp
Privacy Computing Overview
The master teaches you the 3D real-time character production process, the game modeling process sharing
【七夕情人节特效】-- canvas实现满屏爱心