当前位置:网站首页>深度学习秋招面试题集锦(一)
深度学习秋招面试题集锦(一)
2022-07-07 09:34:00 【qinjianhuang】
这部分的面试题包含C++基础知识、python基础、概率相关、智力题相关、算法相关以及深度学习相关。后续还会不断补充,欢迎大家查阅!
Q1 : C++虚函数表剖析。
A1 : CSDN
Q2 : C++中虚析构函数的作用及其原理分析。
A2 : CSDN
Q3 : 结构体(struct)和联合体(union)的区别。
A3 : CSDN
Q4 : Define 和 Const 定义常量的区别。
A4 : CSDN
Q5 : C++ STL。
A5 : CSDN
Q6 : 红黑树概念。
A6 : CSDN
Q7 : 重载与重写的区别。
A7 : CSDN
Q8 : 值传递、指针传递、引用传递详解。
A8 : CSDN
Q9 : 指针与引用的区别。
A9 : CSDN
Q10 : 函数返回时,返回值、返回引用和返回指针的区别。
Q11 : 虚函数能否是内联的?
Q12 : vector和list的区别。
A12 : CSDN
Q13 : C++中的export关键字解释。
A13 : CSDN
Q14 : 私有构造函数的作用。
A14 : CSDN
Q15 : 什么场景下会用到友元函数?
A15 : CSDN
Q16 : 虚函数和纯虚函数的区别?
A16 : CSDN
Q17 : C++内存分配方式详解。
A17 : CSDN
Q1 : Python字典的核心底层原理。
A1 : Python字典的核心底层原理讲解
Q2 : __new__() 与__init__()区别。
A2 : CSDN
Q3 : Python中排序函数sort()和sorted()的区别。
A3 : CSDN
Q1 : 利用牛顿迭代法自己写平方根函数sqrt。
A1 : CSDN
Q2 : 二阶优化方法。
Q3 : 快排算法及其优化。
A3: CSDN
Q4 : 二叉树的前序遍历。
A4 : zhihu
Q5 : 最长子序列。
Q6 : 翻转二叉树。
A6 : zhihu
Q7 : 算法与数据结构中的位运算。
A7 : zhihu
Q8 : 贪心问题(小船过河)。
A8 : CSDN
Q9 : 最长回文子串 & 最长回文子序列(动态规划)。
A9 : CSDN
Q10 : 大数相减(依图祖传题)。
A10 : CSDN
Q11 : 计算从二维数组的左上角到达右下角的所有路径数及最短的那条,如果存在障碍物时又是多少。
A11 : CSDN | 走到(m,n)位置需要m+n-2步,从中选择n-1步向右走,就是组合数 C m + n − 2 n − 1 C^{_{m+n-2}^{n-1}} Cm+n−2n−1
Q12 : 编辑距离及编辑距离算法(动态规划)。
A12 : CSDN
Q13 : 海量数据。
A13 : CSDN
Q14 : 找出未知长度的链表的中间的元素。
A14 : 设置两个指针,p1,p2, 开始p1,p2均位于链表的头部。p1每次前进两步,p2每次前进一步;当p1到达链表的末尾时,p2所在的位置就是链表的中间元素。
Q15 : 删除有序链表中的重复结点。
A15 : CSDN
Q16 : 求数组中出现次数超过数组长度一半的元素。
A16 : CSDN
Q17 : 用1*3的瓷砖密铺3*20的地板有几种方式?(1278)
A17 : 牛客网
Q18 : 顺时针打印矩阵。
A18 : CSDN
Q19 : 字符串循环左移。
A19 : CSDN
Q20 : 给定一个字符串s,你可以从中删除一些字符,使得剩下的串是一个回文串。如何删除才能使得回文串最长呢?
A20 : CSDN
Q21 : 有序数组去重。
A21 : CSDN
Q22 : 子数组的最大累加和。
A22 : CSDN
Q23 : 不借助第三个变量交换a,b两个变量值。
A23 : $a = a + b; b = a - b; a = a - b; $
Q24 : 几种常用排序算法的对比。
A24 : CSDN
Q25 : 42亿QQ,O(1)时间复杂度完成查找。
A25 : CSDN
Q26 : 有排成一行的n个方格,用红(Red)、粉(Pink)、绿(Green)三色涂每个格子,每格涂一色,要求任何相邻的方格不能同色,且首尾两格也不同色.求全部的满足要求的涂法。
A26 : 考虑第n-1个格子:
如果这个格子和第1个格子颜色不同,那么第n个格子只有1种选择,前n-1个格子的选择就是A(n-1),此时n个格子的选择是1*A(n-1)
如果这个格子和第1个格子颜色相同,那么第n个格子只有2种选择,前n-2个格子的选择就是A(n-2),此时n个格子的选择时2*A(n-2)
所以有A(n)=2*A(n-2)+A(n-1), n>=4
remak: 因为我们是考虑第n-1个格子,该格子和第1个格子的颜色可能相同也可能不同,所以n>=4才可以。不然n=3的话,第n-1=3-1=2个格子和第一个格子的颜色必然不同了,就没有上面这2种情况了,所以要从n>=4开始推导。
M 表示色的种数,F(n)是方案数
F(n)=(m-2)(F(n)-1)+(m-1)(F(n)-2)
A(1) = 3
A(2) = 6 //A(3,2)=6
A(3) = 6 //A(3,3)=6
A(n)= A(n-1)+ 2*A(n-2), n>=4
Q27 : 给定整数n和m, 将1到n的这n个整数按字典序排列之后, 求其中的第m个数。
A27 :
既然是字典序,那么很自然,我们可以考虑使用字典树来实现。但是,这里并不需要真的生成这个字典树,而只需要计算对应分支的节点数就行了。计算分支节点数,那么很简单,节点数就是上级节点*10,总的节点数= 1 + (1 * 10) + (1 * 10 * 10) + (1 * 10 * 10 * 10) + … 。
既然知道了如何计算字典树分支的节点数,要想知道第m个数是什么,那么也就是找第m个节点,首先从1开始,如果1分支的节点数>m,那么第m个数肯定是以1开头,进一步搜索其子节点,搜索子节点时不用再搜索1了,所以是搜索1分支的第m-1个节点。如果1分支的节点数<m, 那么所查找的数肯定不是1开头,那么开始搜索2分支,在2分支中,所要找的数应该是第(m-(1分支节点数))个数。重复这个过程,要么搜索子节点,要么搜索兄弟节点,直到最终m==0,也就是当前节点就是所要搜索的节点。
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
while (sc.hasNext()) {
long n = sc.nextLong();
long m = sc.nextLong();
System.out.println(solve(n, m));
}
}
private static long solve(long n, long m) {
long ans = 1;
while (m != 0) {
long cnt = getCntOfPre(ans, n);
if(cnt >= m) {
m --;
if(m == 0)
break;
ans *= 10;
} else {
m -= cnt;
ans ++;
}
}
return ans;
}
// 计算以pre为开头并且小于n的数字的个数
private static long getCntOfPre(long pre, long n) {
long cnt = 1;
long p = 10;
for (; pre * p <= n; p *= 10) {
if (pre * p - 1 + p < n)
cnt += p;
else
cnt += n - pre * p + 1;
}
return cnt;
}
}
Q1 : 用10只小白鼠查找1000瓶药中有毒的那一瓶(只有一瓶)。
A1 : CSDN
Q2 : 卡特兰数。
A2 : 佚名
Q3 : 圆上任取三点构成锐角三角形概率。(1/4)
A3 : 佚名
Q4 : 有两根不均匀的香,烧完一根需要一个小时,如何用两根香来确定一段15分钟的时间?
A4 : 把第一根香两头点燃,同时第二根香的一头点燃,当第一根香烧完的时候是过了半小时,此时把第二根的另一头点燃,从第一根烧完到第二根烧完之间的这段时间是15分钟。
Q5 : 10瓶药,每瓶药都有10颗,其中有一瓶是坏的,质量比正常的多0.1g,如何一次性称出坏的药。
A5 : 分别从1-10号瓶中取1到10颗集中在一起称,看比正常重多少克。
Q6 : 一个房间里面有三盏灯,外面有三个开关,只进去一次怎么确定哪个开关对应哪盏灯。
A6 : 一个开关打开一段时间后关闭,然后打开另一个开关,去房间,摸一下,有温度的是第一个打开的,亮的第二次打开的,另一个灯也就能判断了。
Q7 : 50个红球和50个蓝球,放入两个箱子,怎么样放置才能使拿到红球的概率最大?
A7 : 一个箱子放1个红球,另一个放49个红球和50个蓝球 拿到红球概率=0.5+0.5*(49/99)约等于0.75。
Q8 : 一根木棍截成三段,组成三角形的概率是多少?(1/4)
A8 : 佚名
Q9 : 给一个瞎子52张扑克牌,并告诉他里面恰好有10张牌是正面朝上的.要求这个瞎子把牌分成两堆,使得每堆牌里正面朝上的牌的张数一样多。
A9 : 把扑克牌分成两堆,一堆10张,一堆42张。然后,把小的那一堆里的所有牌全部翻过来。(假设10张中,全部正面朝上,42张中就没有向上的,那么将10张向上的一翻,就变成两边都没有一张向上。若10张中9张向上,42张中则只有1张向上的,那么将10张向上的一翻,就变成两边都各有一张向上,以此类推。)
Q10 : 有 n 份数据,但是 n 的长度并不知道,设计一个采样算法,使得每份被选择的概率是相同的。
A10 : 一开始选择第一个数据作为候选数据,以概率1/2拿第二个数据替换当前候选,以1/3选择拿三个数据替换当前候选,依次类推。这样,第x个数据为最终选择的数据的概率 = x被选择的概率 * (x+1没被选择的概率) * (x+2没有被选择的概率) …(n没有被选择的概率)。举个例子,第2个数据被选择的概率为:1/2 *(2/3 * 3/4 * 4/5 … n-1/n) = 1 / n。
Q11 : n个 [0,n) 的数,求每个数的出现次数(不能开辟额外空间)。
A11 : 这里关键是看清楚题意,n个数,然后是左闭右开的区间,也就是说每个数都不会大于等于n,那么思路主要有以下两点:
1)如果我们给一个索引下的数不管加上多少个n,那么这个数对n取余的话,我们就能知道这个数原来是多少;
2)另一方面,如果一个数出现一次,我们就在对应索引位置下的数加上n,那么每个数对应索引位置上的数对n取商的话,就是这个数出现的次数。这样就做到了没有开辟额外的空间。
public class timeDemo {
public static void main(String[] args){
int[] arr = {0,1,3,4,3,2,5,4,3,7,3,2,4,6};
int n = 8;
for(int i = 0;i<arr.length;i++){
arr[arr[i] % n] += n;
}
for(int i = 0;i<n;i++){
System.out.println(i + ":" + arr[i] / n);
}
}
}
Q12 : 已知有个rand7()的函数,返回1到7随机自然数,怎样利用这个rand7()构造rand10(),随机1~10。
A12 : 产生随机数的主要原则是每个数出现的概率是相等的,如果可以得到一组等概率出现的数字,那么就可以从中找到映射为1~10的方法。
rand7()返回1~7的自然数,构造新的函数 (rand7()-1)*7 + rand7(),这个函数会随机产生1-49的自然数。原因是1-49中的每个数只有唯一的第一个rand7()的值和第二个rand7()的值表示,于是它们出现的概率是相等,均为1/49。
但是这里的数字太多,可以丢弃41-49的数字,把1-40的数字分成10组,每组映射成1-10中的一个,于是可以得到随机的结果。
具体方法是,利用(rand7()-1)*7 + rand7()产生随机数x,如果大于40则继续随机直到小于等于40为止,如果小于等于40,则产生的随机数为(x-1)/4+1。
Q13 : 有一对夫妇,先后生了两个孩子,其中一个孩子是女孩,问另一个孩子是男孩的概率是多大?(2/3)
A13 : 两个孩子的性别有以下四种可能:(男男)(男女)(女男)(女女),其中一个是女孩,就排除了(男男),还剩三种情况。其中另一个是男孩的占了两种,所以答案是2/3。之所以答案不是1/2,是因为女孩到底是第一个生的还是第二个生的是不确定的。
几何分布:
- 做某事件的次数(也叫试验次数)是固定的,用n表示。(例如,抛硬币3次,求婚101次)
- 每一次事件都有两个可能的结果(成功,或者失败)。(例如,求婚被接受(成功),求婚被拒绝(失败))
- 每一次“成功”的概率都是相等的,成功的概率用p表示。
- 这一点也即和二项分布的区别所在,二项分布求解的问题是成功x次的概率。而几何分布求解的问题则变成了试验x次,才取得第一次成功的概率。
几何分布发生的概率: p ( x ) = ( 1 − p ) x − 1 p {p}(x)=(1-p)^{x-1} p p(x)=(1−p)x−1p,期望: 1 p \frac{1}{p} p1
超几何分布:
产品抽样检查中经常遇到一类实际问题,假定在N件产品中有M件不合格品,在产品中随机抽n件做检查,发现k件不合格品的概率为:
P ( X = k ) = C M k C N − M n − k C N n P(X=k)=\frac{C_{M}^{k}C_{N-M}^{n-k}}{C_{N}^{n}} P(X=k)=CNnCMkCN−Mn−k
- 超几何分布和二项分布的区别: 超几何分布需要知道总体的容量,而二项分布不需要;
- 超几何分布是不放回抽取,而二项分布是放回抽取(独立重复) 当总体的容量非常大时,超几何分布近似于二项分布。
伯努利分布:
伯努利分布(Bernoulli distribution)又名两点分布或0-1分布。伯努利分布是离散型概率分布,其概率密度函数为:
f ( x ) = p x ( 1 − p ) 1 − x = { p if x = 1 1 − p if x = 0 0 otherwise f(x)=p^{x}(1-p)^{1-x}=\left\{\begin{array}{ll}{p} & {\text { if } x=1} \\ {1-p} & {\text { if } x=0} \\ {0} & {\text { otherwise }}\end{array}\right. f(x)=px(1−p)1−x=⎩⎨⎧p1−p0 if x=1 if x=0 otherwise
二项分布:
二项分布(Binomial distribution)是n重伯努利试验成功次数的离散概率分布。
P { X = k } = C n k p k ( 1 − p ) n − k P\{X=k\}=C_{n}^{k} p^{k}(1-p)^{n-k} P{ X=k}=Cnkpk(1−p)n−k
期望: E ( X ) = n p E(X)=np E(X)=np,方差: D ( X ) = n p ( 1 − p ) D(X)=np(1-p) D(X)=np(1−p)
几个常用的计算两个概率分布之间距离的方法以及python实现
Q1 : bagging vs boosting vs 随机森林 vs GBDT。
A1 : CSDN
Q2 : 解决局部最优点问题的方案。
A2 :
使用随机梯度下降代替真正的梯度下降。可以这样理解,每次针对单个数据样例进行摸索前进时,本质上是在一个样例形成的误差曲面上摸索前进,而每个样例的曲面大体类似,又不尽相同,当你掉入一个坑里时,往往能被别的曲面拽出来。
设置冲量。人如其名,本次前进的步伐,根据上一次的步伐,适当调大,好比从高处降落的石头,会更有机率跨过一些小坑,如果坑非常大,依靠冲量的惯性是没法逃出的。
不同的初始权值进行训练。假定误差曲面是个坑坑洼洼的曲面,我们尝试第一次降落到随机的起点,然后再开始摸索前进,也许会有运气好的一次,能够不落在某个小坑附近,多次尝试权重,可能会找到好的全局点。
Q1 : Smooth l1 loss和l2有什么区别?
Q2 : Faster RCNN?
A2 : 白裳的文章
Q3 : 优化方法总结(BGD,SGD,Momentum,AdaGrad,RMSProp,Adam)
A3 : CSDN
Q4 : 模型的性能评估标准
A4 : 掘金
Q5 : 深度学习中 number of training epochs 中的 epoch到底指什么?
A5 :
(1)iteration:表示1次迭代(也叫training step),每次迭代更新1次网络结构的参数;
(2)batch-size:1次迭代所使用的样本量;
(3)epoch:1个epoch表示过了1遍训练集中的所有样本。
值得注意的是,在深度学习领域中,常用带mini-batch的随机梯度下降算法训练深层结构,它有一个好处就是并不需要遍历全部的样本,当数据量非常大时十分有效。此时,可根据实际问题来定义epoch,例如定义10000次迭代为1个epoch,若每次迭代的batch-size设为256,那么1个epoch相当于过了2560000个训练样本。
Q6 : 在神经网络中,激活函数sigmoid和tanh除了阈值取值外有什么不同吗?
A6 : Daniel的回答
Q7 : Batch Normalization原理及其好处?
A7 : Juliuszh的文章 | 天雨粟的文章
Q8 : YOLO v1~v3理解?
A8 : YOLO v1深入理解 | YOLO v3深入理解
Q9 : Group Normalization?
A9 : CSDN | DoubleV的文章 | Eminem1147的文章
Q10 : Inception-v1~v4理解?
Q11 : RoIPooling、RoIAlign有什么不同吗?
A11 : CSDN
Q12 : Mask RCNN原理?
A12 : stone的文章
Q13 : 卷积神经网络(CNN)反向传播算法原理?
A13 : BLOG
Q14 : 鞍点解释?
A14 : 夕小瑶的卖萌屋
Q15 : Softmax求导?
A15 : CSDN
Q16 : 神经网络中的各种优化方法?
A16 : CSDN
Q17 : FPN详解。
A17 : CSDN
Q18 : SVM详解。
A18 : CSDN
Q19 : LR为什么取log损失函数,又为什么在似然函数计算之后取对数。
A19 :
(1)损失函数的本质就是,如果我们预测对了,能够不惩罚,如果预测错误,会导致损失函数变得很大,也就是惩罚较大,而-log函数在[-1,1]之间正好符合这一点,另外还有一点需要说明,LR是一种广义的线性回归模型,平方损失函数的话,对于Sigmoid函数求导计算,无法保证是凸函数,在优化的过程中,求得的解有可能是局部最小,不是全局的最优值。其二:取完对数之后,对我们的后续求导比较方便。
(2)如果根据似然函数直接计算,有两点缺点:(1)不利于后续的求导,(2)似然函数的计算会导致下溢出。(最后计算的是相乘的结果,而每个计算之后的值都很小,样本如果很多的情况下,就导致下溢出了。比如 0.01 x 0.01 x 0.01…)
具体推导过程:CSDN
Q20 : LR中的共线性问题和解决方法。
A20 : CSDN
Q21 : LR与SVM异同。
A21 : CSDN
Q22 : SVM的数学基础。
A22 : CSDN
Q23 : 卷积神经网络(CNN)公式推导。
A23 : campoo
Q24 : IOU计算代码。
A24 : Reference
Q25 : Faster RCNN细节。
A25 : BLOG
Q26 : 如何理解空洞卷积(dilated convolution)。
A26 : zhihu
Q27 : 如何理解深度学习中的deconvolution networks。
A27 : zhihu
Q28 : YOLOv2、v3使用K-means聚类计算anchor boxes的具体方法。
A28 : CSDN
Q29 : L1和L2正则化目的是什么,什么含义。
A29 : zhihu
Q30 : KL散度与交叉熵的关系。
A30 : zhihu
Q31 : CNN感受野大小计算。
A31 : CSDN
边栏推荐
- 测试开发基础,教你做一个完整功能的Web平台之环境准备
- The use of list and Its Simulation Implementation
- Shardingsphere sub database and table examples (logical table, real table, binding table, broadcast table, single table)
- 聊聊SOC启动(九) 为uboot 添加新的board
- Unsupervised learning of visual features by contracting cluster assignments
- 90后,辞职创业,说要卷死云数据库
- Distributed database master-slave configuration (MySQL)
- 基于Retrofit框架的金山API翻译功能案例
- Verilog 实现数码管显视驱动【附源码】
- Learning notes | data Xiaobai uses dataease to make a large data screen
猜你喜欢
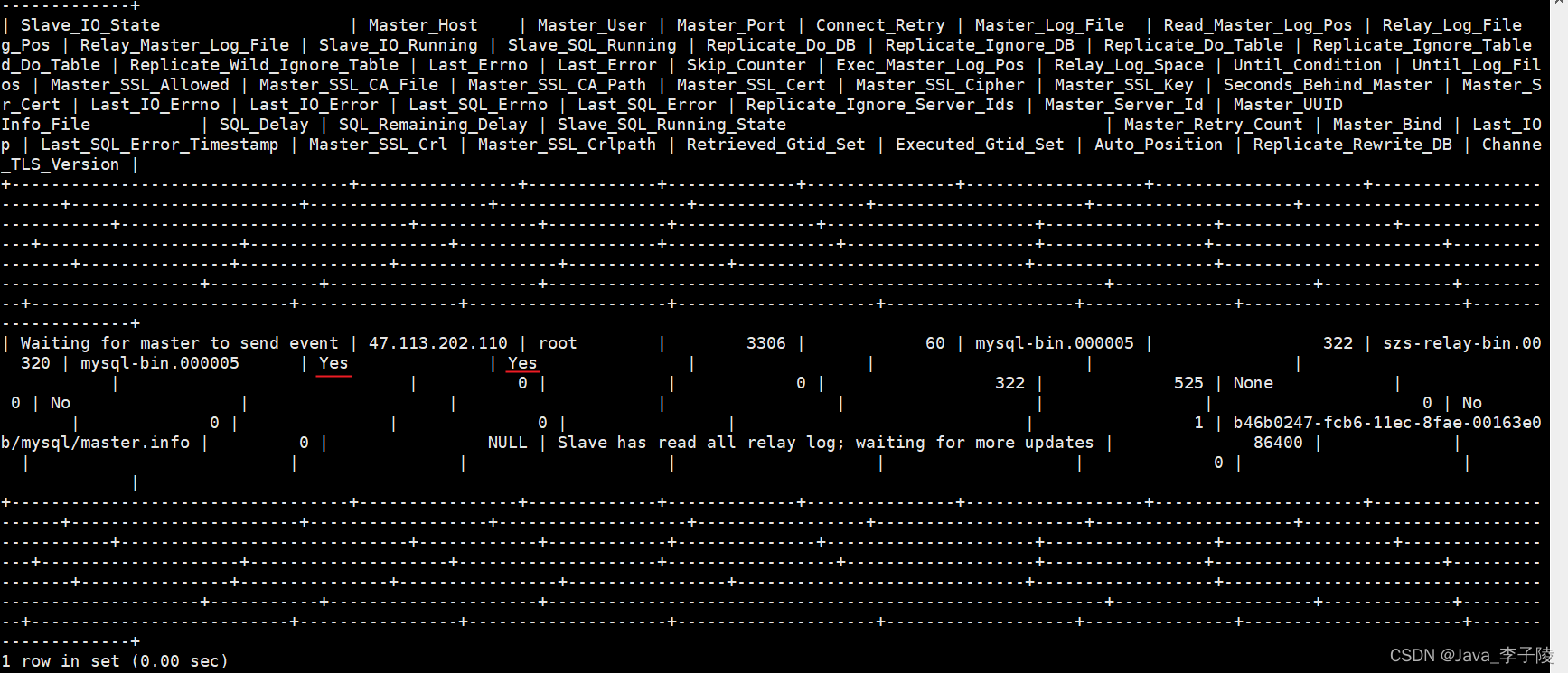
Distributed database master-slave configuration (MySQL)
Antd select selector drop-down box follows the scroll bar to scroll through the solution
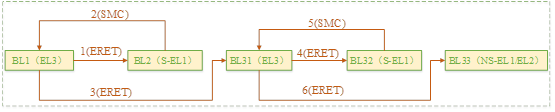
聊聊SOC启动(十) 内核启动先导知识

科普达人丨一文弄懂什么是云计算?

Interprocess communication (IPC)
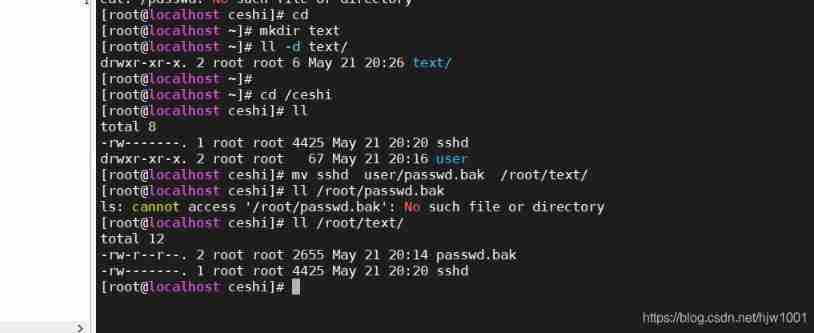
2021-05-21
![[untitled]](/img/f9/18b85ad17d4c560f2b9d95a53ee72a.jpg)
[untitled]
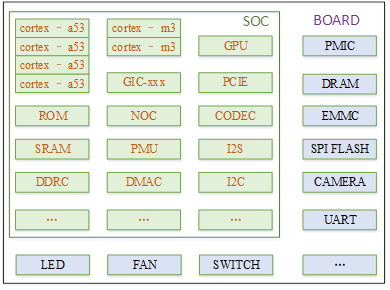
聊聊SOC启动(九) 为uboot 添加新的board
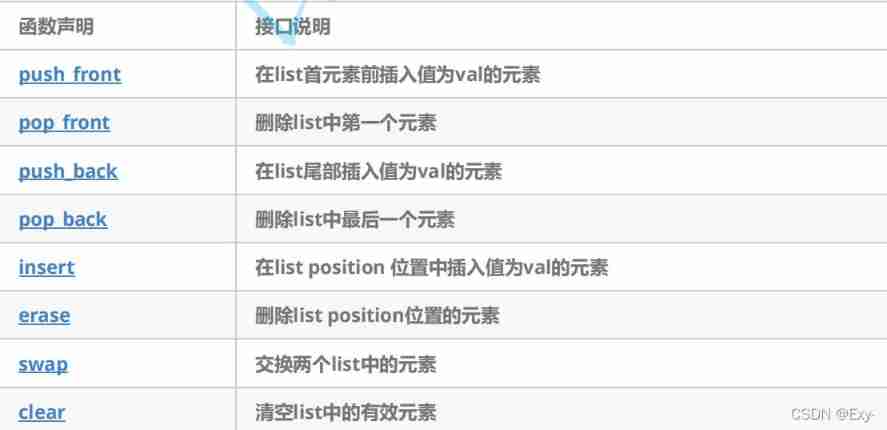
The use of list and Its Simulation Implementation

基于DE2 115开发板驱动HC_SR04超声波测距模块【附源码】
随机推荐
PostgreSQL中的表复制
audit 移植
uniCloud
通过 Play Integrity API 的 nonce 字段提高应用安全性
uniCloud
聊聊SOC启动(十) 内核启动先导知识
【时间格式工具函数的封装】
Force buckle 1002 Find common characters
关于在云服务器上(这里用腾讯云)安装mysql8.0并使本地可以远程连接的方法
Distributed database master-slave configuration (MySQL)
网络协议 概念
2021-05-21
After the uniapp jumps to the page in onlaunch, click the event failure solution
How to remove addition and subtraction from inputnumber input box
RationalDMIS2022阵列工件测量
博客搬家到知乎
Qt|多个窗口共有一个提示框类
Learning notes | data Xiaobai uses dataease to make a large data screen
Process control (creation, termination, waiting, program replacement)
Kitex retry mechanism