[LZY learning notes -dive into deep learning] math preparation 2.5-2.7

2.5 Automatic differentiation

Deep learning framework through ⾃ Calculate the derivative dynamically , namely ⾃ Dynamic differential （automatic differentiation） To speed up the derivation . In the actual , According to the model we designed , The system will build ⼀ Calculation charts （computational graph）, To track which data is calculated and which operations are combined to produce ⽣ Output .
⾃ Dynamic differentiation enables the system to subsequently Back propagation gradient . this ⾥, Back propagation （backpropagate） It means tracking the whole calculation diagram , Fill in the partial derivative of each parameter .
Sharing by a netizen , Explain the calculation diagram and BP
An example

import torch

x = torch.arange(4.0)

#  Not every time ⼀ Allocate new memory when deriving parameters 
#  Because we often update the same parameters thousands of times , Allocating new memory every time may soon run out of memory 
#  A scalar function about a vector x The gradient of is with x Vectors of the same shape 
x.requires_grad_(True)
#  Equivalent to  x=torch.arange(4.0,requires_grad=True)
print(x.grad)

y = 2 * torch.dot(x,x) # y = 2 x⊤ x
print(y)

#  Call the back propagation function to automatically calculate y About x The gradient of each component 
y.backward()
print(x.grad)

# f(x) = 2*x0*x0 + 2*x1*x1 + 2*x2*x2 + 2*x3*x3
# df(x)/dx0 = 4*x0 when x0 = 0, df(x)/dx0 = 0
# df(x)/dx1 = 4*x1 when x1 = 1, df(x)/dx0 = 4
# df(x)/dx2 = 4*x2 when x2 = 2, df(x)/dx0 = 8
# df(x)/dx3 = 4*x3 when x3 = 4, df(x)/dx0 = 12

print(x.grad == 4*x)

#  By default ,PyTorch It accumulates gradients , We need to clear the previous value 
x.grad.zero_()
y = x.sum()
# f(x) = x0 + x1 + x2 + x3
# df(x)/dx0 = df(x)/dx1 = df(x)/dx2 = df(x)/dx3 = 1
y.backward()
print(x.grad)

Back propagation of non scalar variables
When y When it's not scalar , vector y About vectors x The derivative of ⾃ However, the explanation is ⼀ Matrix . about ⾼ Step sum ⾼ Dimensional y and x, The result of derivation can be ⼀ individual ⾼ Order tensor .
Gradient in partial derivative of Advanced Mathematics , The gradient indicates the direction in which a scalar function rises or falls most violently at a certain point and the directional derivative of that direction .

x = torch.arange(4.0,requires_grad=True)
y = x * x #  By element 
#  Yes ⾮ Scalar modulation ⽤backward Need to transmit ⼊⼀ individual gradient Parameters , This parameter specifies the differential function about self Gradient of .
#  Just want to find the sum of partial derivatives , So deliver ⼀ individual 1 The gradient of is appropriate  ( ride 1 Adding up is sum)
y.sum().backward()      # y.backward(torch.ones(len(x)))
print(x.grad)

Separation of computing
You want to move some calculations out of the recorded calculation graph .

import torch

x = torch.arange(4.0,requires_grad=True)
y = x * x #  Non scalar 
u = y.detach()
z = u * x #  Non scalar 
z.sum().backward()
print(x.grad == u) # tensor([True, True, True, True])

x.grad.zero_()
y.sum().backward() #  Non scalar 
print(x.grad == 2 * x) # tensor([True, True, True, True])

Python Gradient calculation of control flow
send ⽤⾃ Dynamic differential ⼀ One advantage is that ： Even if the calculation diagram of the construction function needs to pass Python control flow （ for example , Conditions 、 Loop or any function call ）, We can still calculate the gradient of the variable .

import torch
def f(a):
    b = a * 2
    while b.norm() < 1000:
        b = b * 2
    if b.sum() > 0:
        c = b
    else:
        c = 100 * b
    return c

a = torch.randn(size=(), requires_grad=True)
d = f(a)
d.backward()
print(a.grad == d / a)
# tensor(True)

Summary
Deep learning framework can ⾃ Calculate the derivative dynamically ： We first attach the gradient to the variable on which we want to calculate the partial derivative . Then we record ⽬ Calculation of benchmark value , Execute its back propagation function , And access the resulting gradient .

2.6 probability

Basic probability theory
The process of sampling from the probability distribution is called sampling （sampling）
Assign probability to ⼀ The distribution of some discrete choices is called multinomial distribution （multinomial distribution）
In estimation ⼀ Dice ⼦ The fairness of , We hope from the same ⼀ In distribution ⽣ Into multiple samples . If ⽤Python Of for Loop to complete the task , The speed will be surprisingly slow ⼈. So we make ⽤ The function of the deep learning framework extracts multiple samples at the same time , Get any shape we want ⽴ Sample array .

import torch
from torch.distributions import multinomial
import matplotlib.pyplot as plt

#  A probability distribution 
fair_probs = torch.ones([6]) / 6
#  Sample the data / Sampling 
# sample 600 times with fair probs. theoritical output [100, 100, 100, 100, 100, 100]
print(multinomial.Multinomial(600, fair_probs).sample())

#  Calculate the relative frequency as an estimate of the true probability 
counts = multinomial.Multinomial(1000, fair_probs).sample()
print(counts / 1000)      # theoritical value: 1/6 ~= 0.167

#  How the probability converges to the real probability over time 
#  Into the ⾏500 Group experiment , Extraction of each group 10 Samples 
counts = multinomial.Multinomial(10, fair_probs).sample((500,))
cum_counts = counts.cumsum(dim=0) #  Add by line 
estimates = cum_counts / cum_counts.sum(dim=1, keepdims=True) #  Keep the shape without dimension reduction 
print(estimates)

#  draw 6 line 
for i in range(6):
    plt.plot(estimates[:, i].numpy(), label=("P(die=" + str(i + 1) + ")"))

plt.axhline(y=0.167, color='black', linestyle='dashed') # axhline Draw parallel to x Horizontal reference line of axis 
plt.gca().set_xlabel("Groups of experiments")
plt.gca().set_ylabel("Estimated probability")
plt.legend() #  Add icons 
plt.show()

axiom ：
When processing the roll of dice , We will gather S = {1, 2, 3, 4, 5, 6} Called sample space （sample space） Or result space （outcome
space）, Each of these elements is the result （outcome）
event （event） yes ⼀ Random results of a given set of sample spaces

A random variable ：

Discrete random variable vs Continuous random variables （ Section ）
In these cases , We quantify the probability of seeing a certain value as density （density）. The height is just 1.80 The probability of meters is 0, But density is not 0.
Handle multiple random variables
① joint probability joint probability P(A = a, B = b)
A = a and B = b At the same time ⽣ The possibility is not ⼤ On A = a or B = b Single issue ⽣ The possibility of
② Conditional probability conditional probability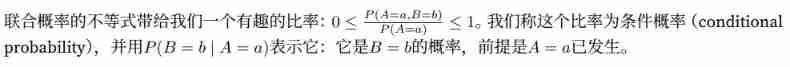

③ Bayes theorem Bayes’theorem

④ Marginalization

⑤ independence
rely on （dependence） And alone ⽴（independence）
If two random variables A and B It's the only one ⽴ Of , It means events A The hair of ⽣ Follow B The occurrence of events ⽣⽆ Turn off .
Two random variables are unique ⽴ Of , If and only if the joint distribution of two random variables is their respective ⾃ The product of the distribution .

Expectation and variance ： Summarize the key characteristics of probability distribution

⼩ junction
• We can sample from the probability distribution .
• We can make ⽤ Joint distribution 、 Conditional distribution 、Bayes Theorem 、 Marginalization and independence ⽴ Sex hypothesis to analyze multiple random variables .
• Expectations and ⽅ Difference provides a real basis for the generalization of the key characteristics of probability distribution ⽤ Measurement form of .

2.7 Consult the documentation

Find all functions and classes in the module
Usually , We can ignore it by “__”（ Double underline ） Start and end functions （ They are Python Special objects in ）, Or in a single “_”（ Underline ） Start function （ They are usually internal functions ）.

import torch
#  see PyTorch API Guidance of 

#  Query random numbers ⽣ All attributes in the module 
print(dir(torch.distributions)) #  Adjustable in the module ⽤ Which functions and classes 

Find the usage of specific functions and classes

import torch
#  How to make ⽤ A more specific description of a given function or class 

#  Look at the tensor ones function 
help(torch.ones)

⼩ junction
• Officer, ⽅⽂ Files provide information beyond this book ⼤ Quantity description and ⽰ example .
• We can adjust ⽤dir and help Function or in Jupyter Make... In Notepad ⽤? and ?? see API Of ⽤ Law ⽂ files .