分子个数 数论（欧拉函数 前缀和

题面：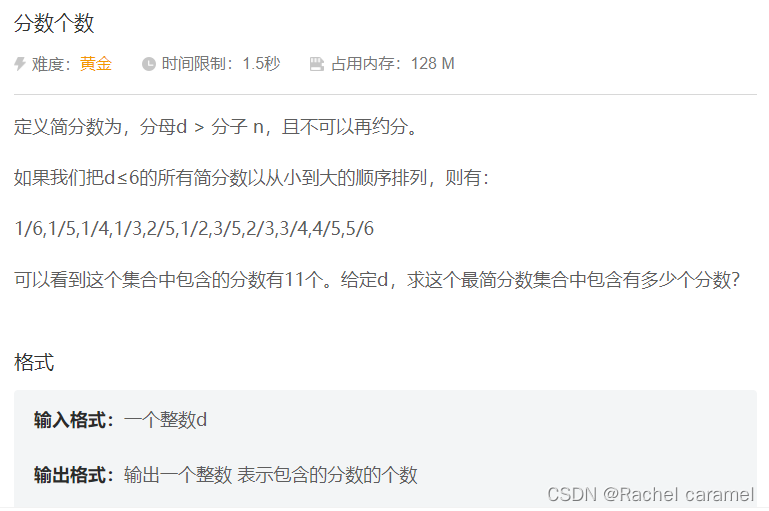


思路：
题目的意思其实就是求 欧拉函数的前缀和
$$\begin{gathered} \sum _{i=2}^d\sum _{j=1}^{j=i-1}[\gcd (j,i)=1] \\ \text{注：}[\gcd (j,i)=1]\text{的含义为:} \\ \text{若}\gcd (j,i)=1，[\gcd (j,i)=1]=1 \\ \text{若}\gcd (j,i)\ne 1，[\gcd (j,i)=1]=0 \end{gathered}$$
欧拉函数的各种推导可见欧拉函数总结
代码：

#include <bits/stdc++.h>
#include <iostream>
using namespace std;
const int maxn=111111;
int d;
long long ans,phi[maxn];

void handle(int n)
{
    
    for(int i=1;i<=n;i++) phi[i]=i;
    for(int i=2;i<=n;i++)
    {
    
        if(phi[i]==i)
        {
    
            for(int j=i;j<=n;j+=i) phi[j]=phi[j]-phi[j]/i;
        }
    }
}

int main()
{
    
    scanf("%d",&d);
    handle(d);
    for(int i=2;i<=d;i++) ans+=phi[i];
    printf("%lld\n",ans);
	return 0;
}