当前位置:网站首页>(POJ - 2739) sum of constructive prime numbers (ruler or two points)
(POJ - 2739) sum of constructive prime numbers (ruler or two points)
2022-07-06 16:09:00 【AC__ dream】
Topic link :Sum of Consecutive Prime Numbers - POJ 2739 - Virtual Judge
Chinese question meaning :
Small X I like prime numbers very much , So we often study the properties of primes , That day he wanted to know whether a number could be used ( Maybe it's a ) The sum of consecutive prime numbers represents , And want to know how many ways . for example ,53 There are two ways to express 5 + 7 + 11 + 13 + 17 and 53. Prime number v Must be continuous and a prime can only be used once . Now I'll give you an integer n, You have to tell him how many different continuous primes and representations there are for this number .
Input
Multiple sets of data input , One number per line n, When n=0 End of time . n stay 2 And 10000 Between .
Output
One line per output , Output the corresponding answer .
Sample Input
2 3 17 41 20 666 12 53 0
Sample Output
1 1 2 3 0 0 1 2
analysis : There are two approaches to this topic , The following two methods are analyzed respectively
No matter which method is used, the prime table needs to be preprocessed ,10000 The prime number table of can be pretreated with Ehrlich sieve
The first way : Ruler method
We use it l and r Represents the sum of the currently selected primes , If less than n, Just make r Add one , If more than n Just make l reduce 1, If the sum of the currently selected primes is equal to n, Makes the ans+1, This will solve the problem , This method is relatively simple , Complexity is o(nlogn)( Because the complexity of the sieve is nlogn), It's also easier to implement
The second way : Two points
We preprocess the prefixes of primes and , Fix the right boundary every time r, Judging whether there is a left boundary satisfying the meaning of the question by dichotomy left boundary makes l To r The sum of primes in is n, The overall complexity is also o(logn), To optimize a little bit of code , We can dichotomy the bounded maximum in advance , Because the maximum value of the continuous primes we choose must be less than or equal to n Of , So we can choose the first one less than or equal to n As the right boundary , This process is realized by dichotomy , The overall complexity is also o(nlogn), It is complex to realize the method of larger scale
Here are the codes of two methods :
Ruler method :
#include<cstdio>
#include<iostream>
#include<cstring>
#include<vector>
#include<algorithm>
#include<map>
#include<cmath>
#include<queue>
using namespace std;
const int N=10003;
int prime[N],cnt,s[N];
bool vis[N];
void init()// Preprocess out primes
{
for(int i=2;i<=10000;i++)
{
if(vis[i]) continue;
prime[++cnt]=i;
for(int j=2;j*i<=10000;j++)
vis[i*j]=true;
}
}
int main()
{
init();
int n;
while(1)
{
scanf("%d",&n);
if(!n) break;
int ans=0,p=0;
for(int i=1,j=1;i<=cnt&&j<=cnt;)
{
while(p<n&&j<=cnt) p+=prime[j++];
if(p==n) ans++,p-=prime[i++];
else while(p>n) p-=prime[i++];
if(p==n) ans++,p-=prime[i++];
if(prime[j]>n) break;
}
printf("%d\n",ans);
}
return 0;
}Dichotomy :
#include<cstdio>
#include<iostream>
#include<cstring>
#include<vector>
#include<algorithm>
#include<map>
#include<cmath>
#include<queue>
using namespace std;
const int N=10003;
int prime[N],cnt,s[N];
bool vis[N];
void init()// Preprocess out the prime prefix and
{
for(int i=2;i<=10000;i++)
{
if(vis[i]) continue;
prime[++cnt]=i;
for(int j=2;j*i<=10000;j++)
vis[i*j]=true;
}
for(int i=1;i<=cnt;i++)
s[i]=s[i-1]+prime[i];
}
bool check(int x,int rr)// see x Can it be regarded as No rr The continuous sum of primes at the end of primes
{
int l=0,r=rr-1,mid;
while(l<r)
{
mid=l+r+1>>1;
if(s[rr]-s[mid]>=x) l=mid;
else r=mid-1;
}
if(s[rr]-s[l]==x) return true;
return false;
}
int main()
{
init();
int n;
while(1)
{
scanf("%d",&n);
if(!n) break;
int l=1,r=cnt,mid;
while(l<r)// Find out if it is less than or equal to x The first prime of
{
mid=l+r+1>>1;
if(prime[mid]<=n) l=mid;
else r=mid-1;
}
int ans=0;
for(int i=1;i<=r;i++)
ans+=check(n,i);
printf("%d\n",ans);
}
return 0;
}边栏推荐
- 渗透测试 ( 3 ) --- Metasploit Framework ( MSF )
- [exercise-3] (UVA 442) matrix chain multiplication
- Borg maze (bfs+ minimum spanning tree) (problem solving report)
- Opencv learning log 24 -- Hough transform 2 (maximum interval and minimum length can be limited)
- Perform general operations on iptables
- 【练习-5】(Uva 839)Not so Mobile(天平)
- C language must memorize code Encyclopedia
- Shell脚本编程
- Pyside6 signal, slot
- Information security - Analysis of security orchestration automation and response (soar) technology
猜你喜欢
Nodejs+vue online fresh flower shop sales information system express+mysql
Quick to typescript Guide
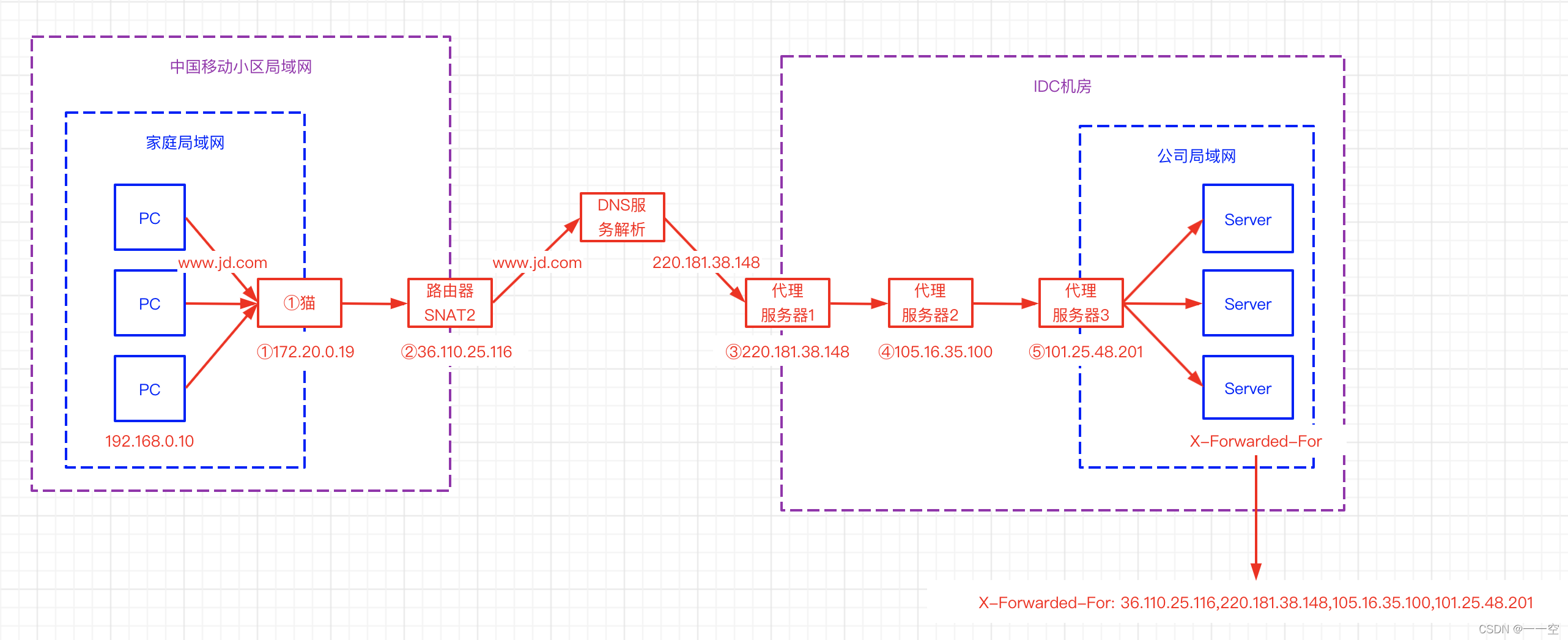
X-forwarded-for details, how to get the client IP
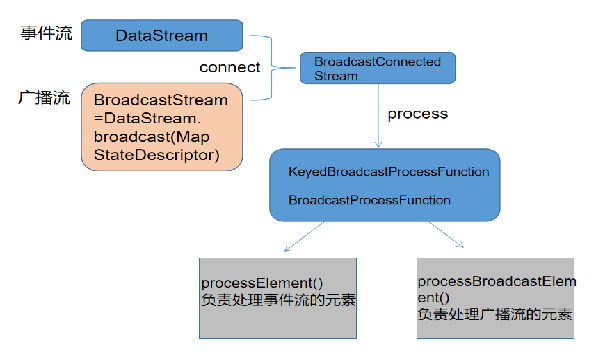
信息安全-威胁检测-flink广播流BroadcastState双流合并应用在过滤安全日志
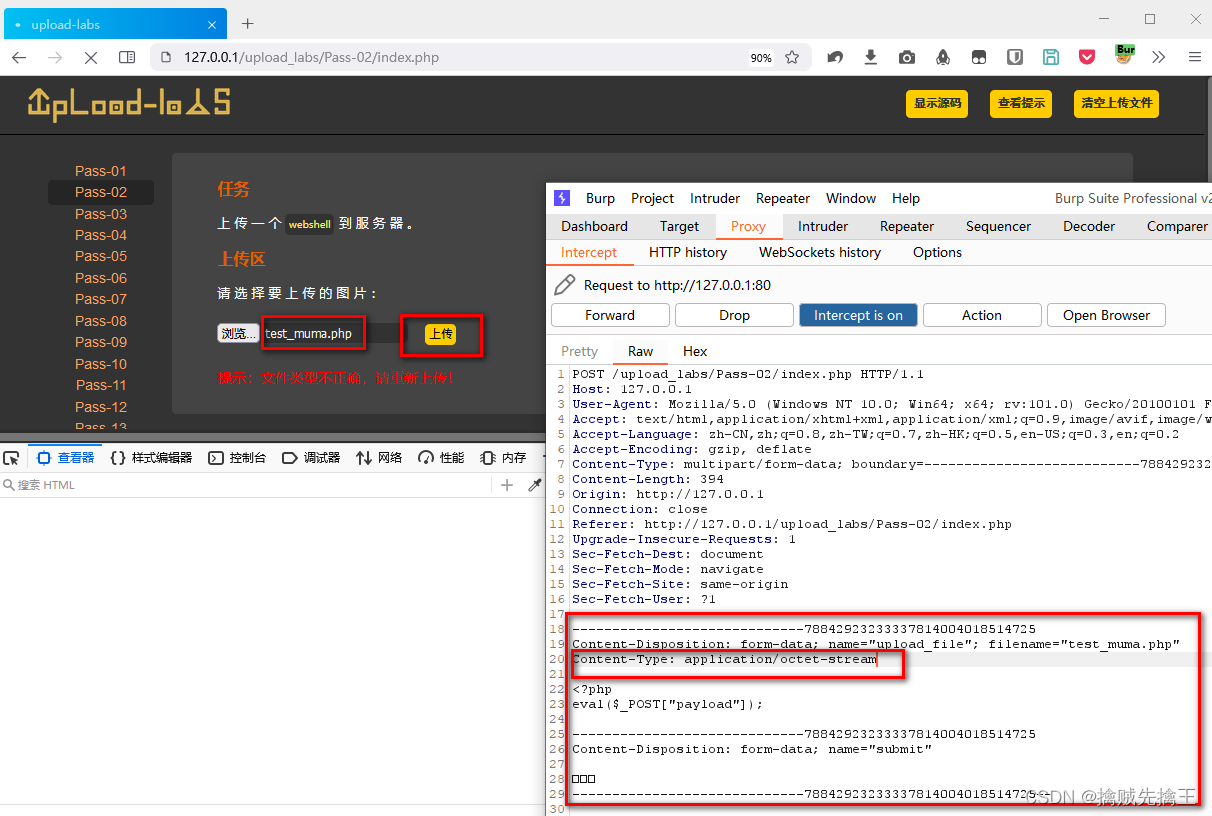
渗透测试 2 --- XSS、CSRF、文件上传、文件包含、反序列化漏洞
1005. Maximized array sum after K negations
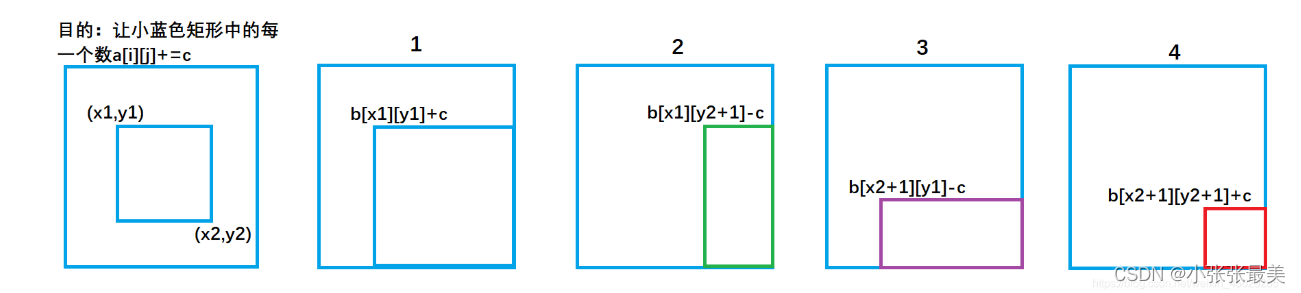
Differential (one-dimensional, two-dimensional, three-dimensional) Blue Bridge Cup three body attack

【练习-4】(Uva 11988)Broken Keyboard(破损的键盘) ==(链表)
b站 实时弹幕和历史弹幕 Protobuf 格式解析
信息安全-威胁检测-NAT日志接入威胁检测平台详细设计
随机推荐
[exercise-3] (UVA 442) matrix chain multiplication
Web based photo digital printing website
1903. Maximum odd number in string
Information security - Epic vulnerability log4j vulnerability mechanism and preventive measures
X-Forwarded-For详解、如何获取到客户端IP
Flink 使用之 CEP
b站 实时弹幕和历史弹幕 Protobuf 格式解析
Research Report on shell heater industry - market status analysis and development prospect forecast
Opencv learning log 32 edge extraction
2078. Two houses with different colors and the farthest distance
最全编程语言在线 API 文档
【练习-11】4 Values whose Sum is 0(和为0的4个值)
Opencv learning log 15 count the number of solder joints and output
【练习-4】(Uva 11988)Broken Keyboard(破损的键盘) ==(链表)
Research Report of peripheral venous catheter (pivc) industry - market status analysis and development prospect prediction
Hdu-6025-prime sequence (girls' competition)
Interval sum ----- discretization
Borg Maze (BFS+最小生成树)(解题报告)
[exercise -10] unread messages
B - 代码派对(女生赛)