数组中的第K大元素[堆排 + 建堆的实际时间复杂度]

前言

堆排可以不用完全排序，再取第K大元素，但是选择排序也亦如此。

那么谁会运行的更快呐？建堆时，需要调整n/2次，每次最大深度为log₂(n)，第一直观印象就是建堆T(n) = O(nlgon)，其实不然。

堆排取k大元素的时间 = 建堆时间 + 取k个元素的时间 = (O(n) - O(log₂n) - 1) + O(klog₂n) = O(n);
选择排序取k大元素的时间 = O(kn) = O(n).

因为(O(n) - O(log₂n) - 1) + O(klog₂n) <O(kn)，所以堆排要快些。

证明在第二部分代码前的注释中。

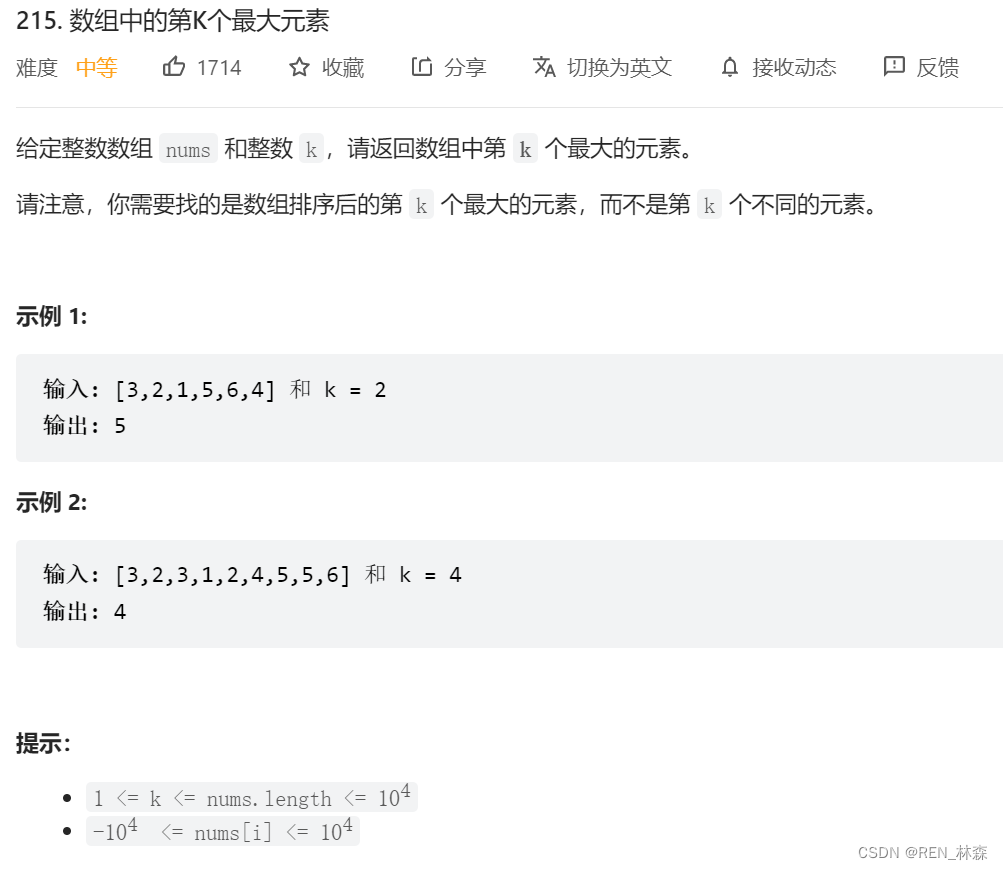
一、数组中的第K大元素

二、建堆复杂度证明

证明：以最多节点的满二叉树为例，树高为h，

设当前层为k，则该层有2^(k - 1)^个节点，每个节点需要调整h - k的深度。

所以，T(n) = 2⁰ * (h - 1) + 2¹ * (h - 2) +…+2^(h - 2) * 1,显然是一个典型的差比数列，只需错位相减即可。

2T(n) = 2¹ * (h - 1) + 2² * (h - 2) +…+2^(h - 2)^ * 2 + 2^(h - 1) * 1,

两式差得T(n) = 2^h - h - 1，注：h = log2(n)，所以T(n) = O(n) - O(log2(n)) - 1 = O(logn)

注：计算复杂度，前提条件就是n足够大，如果n很小，就无复杂度可言，直接O(1)

三、快排/优先队列/堆排

package everyday.medium;

import java.util.PriorityQueue;

// 数组中第k个最大元素。
public class FindKthLargest {
    /* target：取数组中第K大元素，把数组排个序，取nums[k - 1]即可，但时间复杂度O(nlogn)，不可取。 选择排序，选择第K个，时间复杂度O(kn),即O(n)，可行。 堆排，建堆要花O(nlogn)，选第k大，花O(klogn),时间复杂度O( )，不可行。 为什么建堆要花O(nlogn)？我们直观的感觉，要调整n/2次(从倒数第二行开始调整)，每次调整向下O(logn)(自然而然取了最大的一次)。 所以建堆要花O(nlogn)。但是这是错觉。实际的时间复杂度为Tn = 2^log2(n)^ - log2(n) - 1 =O(n) - O(logn) = O(n)(当n很大时) 证明：以最多节点的满二叉树为例，树高为h， 设当前层为k，则该层有2^(k - 1)^个节点，每个节点需要调整h - k的深度。 所以，T(n) = 2^0^ * (h - 1) + 2^1^ * (h - 2) +...+2^(h - 2) * 1,显然是一个典型的差比数列，只需错位相减即可。 2T(n) = 2^1^ * (h - 1) + 2^2^ * (h - 2) +...+2^(h - 2)^ * 2 + 2^(h - 1) * 1, 两式差得T(n) = 2^h^ - h - 1,注：h = log2(n),所以T(n) = O(n) - O(log2(n)) - 1 = O(logn) 注：计算复杂度，前提条件就是n足够大，如果n很小，就无复杂度可言，直接O(1) */
    // 选择排序 -- 虽然是O(n),但时间是Tn = kn,比起堆排，Tn = n - log(n+1) + klogn,还是要慢很多。
    public int findKthLargest(int[] nums, int k) {
        for (int i = 0; i < k; i++) {
            // 选择
            int max = nums[i], idx = i;
            for (int j = i + 1; j < nums.length; j++) {
                if (max < nums[j]) {
                    max = nums[j];
                    idx = j;
                }
            }
            // swap
            int t = nums[idx];
            nums[idx] = nums[i];
            nums[i] = t;
        }
        // 取值
        return nums[k - 1];
    }

    // 堆排，熟练API，优先队列，整个大顶堆。
    public int findKthLargest2(int[] nums, int k) {
        // 大顶堆
        PriorityQueue<Integer> que = new PriorityQueue<>((o1, o2) -> o2 - o1);
        // 加入元素
        for (int num : nums) que.offer(num);
        // 把第1 - (k-1)大的元素取出
        for (int i = 0; i < k - 1; i++) que.poll();
        // 取第K大
        return que.poll();
    }

    // 堆排，API有太多累赘的地方，直接堆排。
    public int findKthLargest3(int[] nums, int k) {
        // 建堆，从倒数第二层有孩子的节点开始调整。
        for (int i = nums.length - 1 >>> 1; i >= 0; i--) adjustHeap(nums, i, nums.length);
        // 排前K个大元素出来。
        int i = 0;
        do {
            // swap
            int t = nums[0];
            nums[0] = nums[nums.length - 1 - i];
            nums[nums.length - 1 - i] = t;
            // 调整堆，让堆顶为最大元素。
            if (++i >= k) break;
            adjustHeap(nums, 0, nums.length - i);
        } while (true);
        // 取第k个最大元素
        return nums[nums.length - k];
    }

    // 堆排核心：调整堆
    private void adjustHeap(int[] nums, int k, int end) {
        int ori = nums[k]; // 记住要调整的原始元素。
        // 不断向下调整
        for (int i = (k << 1) + 1; i < end; i = (i << 1) + 1) {
            // 看左孩子还是右孩子大。
            if (i + 1 < end && nums[i + 1] > nums[i]) ++i;
            // 看是否有必要和孩子交换。
            if (ori >= nums[i]) break;
            // 向下调整
            nums[k] = nums[i];
            // 得到原始元素的新位置。
            k = i;
        }
        // 把原始元素放到它最后交换到的空位上。
        nums[k] = ori;
    }
}

总结

1）堆排建堆的时间复杂度是O(n)，不是O(nlogn).
2）优先队列/堆排/选择排序。

参考文献

LeetCode 数组中的第K大元素