当前位置:网站首页>[combinatorics] recursive equation (general solution structure of recursive equation with multiple roots | linear independent solution | general solution with multiple roots | solution example of recu
[combinatorics] recursive equation (general solution structure of recursive equation with multiple roots | linear independent solution | general solution with multiple roots | solution example of recu
2022-07-03 17:06:00 【Programmer community】
List of articles
- One 、 Linear independent solution
- Two 、 There is a general solution under the double root
- Two 、 There is a general solution under the double root
- 3、 ... and 、 Examples of solving recursive equations with multiple roots
- Four 、 Summary of the solution of recurrence equation formula
One 、 Linear independent solution
Linear independent solution :
If
q
q
q It's a recursive equation
e
e
e Heavy characteristic root , be
q
n
,
n
q
n
,
n
2
q
n
,
⋯
,
n
e
−
1
q
n
q^n , nq^n , n^2q^n , \cdots , n^{e-1}q^n
qn,nqn,n2qn,⋯,ne−1qn
It's a recursive equation Linearly independent solutions ;
e
e
e Is the multiplicity of the characteristic root ;
Two 、 There is a general solution under the double root
q
1
,
q
2
,
⋯
,
q
t
q_1, q_2, \cdots , q_t
q1,q2,⋯,qt It's a recursive equation Unequal characteristic roots , Yes
t
t
t Unequal characteristic roots ,
q
i
q_i
qi The multiplicity of is
e
i
e_i
ei ,
A characteristic root
q
i
q_i
qi , Its repeatability is
e
i
e_i
ei , The Characteristic root Corresponding Items in the general solution yes :
H
i
(
n
)
=
(
c
i
1
+
c
i
2
n
+
⋯
+
c
i
e
i
n
e
i
−
1
)
q
i
n
H_i(n) = (c_{i1} + c_{i2}n + \cdots + c_{ie_i}n^{e_i - 1})q_i^n
Hi(n)=(ci1+ci2n+⋯+cieinei−1)qin
Of the above general solution Coefficient , contain
e
i
e_i
ei The item , this
e
i
e_i
ei Beyond the constants of the terms
n
n
n The power is taken from
0
0
0 To
e
i
−
1
e_i - 1
ei−1 ,
The general solution of the recurrence equation is :
H
(
n
)
=
∑
i
=
1
t
H
i
(
n
)
H(n) = \sum\limits_{i=1}^tH_i(n)
H(n)=i=1∑tHi(n)
Two 、 There is a general solution under the double root
The general solution form under the double root is listed :
1 . Number of characteristic elements :
q
1
,
q
2
,
⋯
,
q
t
q_1, q_2, \cdots , q_t
q1,q2,⋯,qt Is the characteristic root of recursive equation , Unequal characteristic roots
t
t
t ;
2 . according to Characteristic root Write the items in the general solution
H
i
(
n
)
H_i(n)
Hi(n) : Characteristic root
q
i
q_i
qi , Repeatability
e
i
e_i
ei , among
i
i
i The value is
0
0
0 To
t
t
t; The first
i
i
i The general solution term corresponding to characteristic roots , Write it down as
H
i
(
n
)
H_i(n)
Hi(n) ;
- ( 1 ) form : Coefficient term multiply
q
i
n
q_i^n
qin ;
- ( 2 ) Coefficient term :
- ① Number : Yes
e
i
e_i
ei term ; Number of coefficient terms , Is the repeatability of the characteristic root ;
- ② form : constant multiply
n
n
n
e
i
−
1
n^{e_i-1}
nei−1 , Here you are
e
i
e_i
ei It's a constant ;
- 1 > constant : The constant subscript is from
c
i
1
c_{i1}
ci1 To
c
i
e
i
c_{ie_i}
1
1
1 To
e
i
e_i
ei ;
ciei , The right part of the subscript is
- 2 >
n
n
0
0
0 To
e
i
−
1
e_i - 1
ei−1 ;
n Power of power : The value of power is from
- 3 > Suggested arrangement : constant and The next power , It's best to arrange them from small to large , Constant subscript And
n
n
n The power of Difference between
1
1
1 ;
n Power of power ; Such as :
- 1 > constant : The constant subscript is from
- ① Number : Yes
- ( 3 ) General explanation
i
i
H
i
(
n
)
=
(
c
i
1
+
c
i
2
n
+
⋯
+
c
i
e
i
n
e
i
−
1
)
q
i
n
H_i(n) = (c_{i1} + c_{i2}n + \cdots + c_{ie_i}n^{e_i - 1})q_i^n
Hi(n)=(ci1+ci2n+⋯+cieinei−1)qin
i term :
3 . Write a general solution :
- ( 1 ) Number of general solutions : Number of characteristic elements
t
t
t ;
- ( 2 ) General solution composition : The general solution term corresponding to each characteristic root , Put it all together , Is the complete general solution ;
- ( 3 ) final result :
H
(
n
)
=
∑
i
=
1
t
H
i
(
n
)
H(n) = \sum\limits_{i=1}^tH_i(n)
H(n)=i=1∑tHi(n)
3、 ... and 、 Examples of solving recursive equations with multiple roots
Solution :
1 . Characteristic equation :
( 1 ) The standard form of recurrence equation : Write the recurrence equation Standard form , All items are to the left of the equal sign , On the right is
0
0
0 ;
The recursive equation is now in standard form ;
( 2 ) Number of terms of characteristic equation : determine Number of terms of characteristic equation , And The recurrence equation has the same number of terms ;
5
5
5 term ;
( 3 ) The characteristic equation is sub idempotent : The highest power is Number of terms of characteristic equation
−
1
-1
−1 , Lowest power
0
0
0 ;
x
x
x The power of is from
0
0
0 To
4
4
4 ;
( 4 ) Write There is no coefficient The characteristic equation of ;
x
4
+
x
3
+
x
2
+
x
+
1
=
0
x^4 + x^3 + x^2 + x + 1 = 0
x4+x3+x2+x+1=0
( 5 ) The coefficients of the recursive equation will be deduced bit by bit Copy Into the characteristic equation ;
x
4
+
x
3
−
3
x
2
−
5
x
−
2
=
0
x^4 + x^3 - 3x^2 -5 x -2 = 0
x4+x3−3x2−5x−2=0
2 . Solution characteristic root : take Characteristic equation Characteristic root Work it out ,
x
=
−
b
±
b
2
−
4
a
c
2
a
x = \cfrac{-b \pm \sqrt{b^2 - 4ac}}{2a}
x=2a−b±b2−4ac
The characteristic root solved is
−
1
,
−
1
,
−
1
,
2
-1, -1, -1, 2
−1,−1,−1,2 ;
3 . Construct the general solution of recurrence equation :
( 1 ) No double root : structure
c
1
q
1
n
+
c
2
q
2
n
+
⋯
+
c
k
q
k
n
c_1q_1^n + c_2q_2^n + \cdots + c_kq_k^n
c1q1n+c2q2n+⋯+ckqkn Linear combination of forms , This linear combination is the of recursive equations general solution ;
( 2 ) Double root : Refer to the following “ The general solution form under the double root is listed ” Content ;
The situation here belongs to the situation with double roots , Refer to the following solution :
Heavy root
−
1
-1
−1 Items need to be in accordance with The general solution rule of multiple roots Write ;
Non double root
2
2
2 , May, in accordance with the The general form Write , namely
c
4
2
n
c_42^n
c42n ,
c
4
c_4
c4 Is constant ,
4
4
4 This is the number
4
4
4 A characteristic root ;
The heavy root is
−
1
-1
−1 , The repeatability is
3
3
3 ;
H
1
(
n
)
H_1(n)
H1(n) Represents the heavy root item , This item is composed of Coefficient term multiply
(
−
1
)
n
(-1)^n
(−1)n form ;
There is
3
3
3 term ; The form of each coefficient term is constant multiply
n
n
n The power of ;
Constant use
c
1
,
c
2
,
c
3
c_1, c_2, c_3
c1,c2,c3 Express ,
n
n
n The power of The value is
0
0
0 To
2
2
2 ( Number of coefficient terms
−
1
-1
−1 ) ;
Write
−
1
-1
−1 The general solution term corresponding to the characteristic root :
H
1
(
n
)
=
(
c
1
+
c
2
n
+
c
3
n
2
)
(
−
1
)
n
H_1(n) = (c_1 + c_2n + c_3n^2)(-1)^n
H1(n)=(c1+c2n+c3n2)(−1)n
The complete general solution is :
H
(
n
)
=
(
c
1
+
c
2
n
+
c
3
n
2
)
(
−
1
)
n
+
c
4
2
n
H(n) = (c_1 + c_2n + c_3n^2)(-1)^n + c_42^n
H(n)=(c1+c2n+c3n2)(−1)n+c42n
4 . Find the constant in the general solution :
( 1 ) Substitute the initial values to obtain the equations : Substitute the initial value of the recursive equation into the general solution , obtain
k
k
k individual
k
k
k Finite element equations , adopt Solve the equations , obtain Constants in general solutions ;
{
(
c
1
+
0
c
2
+
0
2
c
3
)
(
−
1
)
0
+
2
0
c
4
=
F
(
0
)
=
1
(
c
1
+
1
c
2
+
1
2
c
3
)
(
−
1
)
1
+
2
1
c
4
=
F
(
1
)
=
0
(
c
1
+
2
c
2
+
2
2
c
3
)
(
−
1
)
2
+
2
2
c
4
=
F
(
2
)
=
1
(
c
1
+
3
c
2
+
3
2
c
3
)
(
−
1
)
3
+
2
3
c
4
=
F
(
3
)
=
2
\begin{cases} ( c_1 + 0c_2 + 0^2c_3 )(-1)^0 + 2^0c_4 = F(0) = 1 \\\\ ( c_1 + 1c_2 + 1^2c_3 )(-1)^1 + 2^1c_4 = F(1) = 0 \\\\ ( c_1 + 2c_2 + 2^2c_3 )(-1)^2 + 2^2c_4 = F(2) = 1 \\\\ ( c_1 + 3c_2 + 3^2c_3 )(-1)^3 + 2^3c_4 = F(3) = 2 \end{cases}
⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧(c1+0c2+02c3)(−1)0+20c4=F(0)=1(c1+1c2+12c3)(−1)1+21c4=F(1)=0(c1+2c2+22c3)(−1)2+22c4=F(2)=1(c1+3c2+32c3)(−1)3+23c4=F(3)=2
It is reduced to :
{
c
1
+
c
4
=
1
−
c
1
−
c
2
−
c
3
+
2
c
4
=
0
c
1
+
2
c
2
+
4
c
3
+
4
c
4
=
1
−
c
1
−
3
c
2
−
9
c
3
+
8
c
4
=
2
\begin{cases} c_1 +c_4= 1 \\\\ -c_1 - c_2 - c_3 + 2c_4 = 0 \\\\ c_1 +2 c_2 +4 c_3 + 4c_4= 1 \\\\ -c_1 - 3c_2 - 9c_3 + 8c_4= 2 \end{cases}
⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧c1+c4=1−c1−c2−c3+2c4=0c1+2c2+4c3+4c4=1−c1−3c2−9c3+8c4=2
Solve the above
4
4
4 The constant value is :
c
1
=
7
9
,
c
2
=
−
1
3
,
c
3
=
0
,
c
4
=
2
9
c_1 = \cfrac{7}{9}, c_2 = -\cfrac{1}{3}, c_3 = 0, c_4 = \cfrac{2}{9}
c1=97,c2=−31,c3=0,c4=92
( 2 ) Substitute constants to obtain the general solution : Substitute constants into the general solution , You can get the final solution of the recursive equation ;
Complete general solution :
H
(
n
)
=
7
9
(
−
1
)
n
−
1
3
(
−
1
)
n
+
2
9
2
n
H(n) = \cfrac{7}{9} (-1)^n - \cfrac{1}{3} (-1)^n + \cfrac{2}{9}2^n
H(n)=97(−1)n−31(−1)n+922n
Four 、 Summary of the solution of recurrence equation formula
The whole process of solving recursive equations :
1 . Characteristic equation :
( 1 ) The standard form of recurrence equation : Write the recurrence equation Standard form , All items are to the left of the equal sign , On the right is
0
0
0 ;
( 2 ) Number of terms of characteristic equation : determine Number of terms of characteristic equation , And The recurrence equation has the same number of terms ;
( 3 ) The characteristic equation is sub idempotent : The highest power is Number of terms of characteristic equation
−
1
-1
−1 , Lowest power
0
0
0 ;
( 4 ) Write There is no coefficient The characteristic equation of ;
( 5 ) The coefficients of the recursive equation will be deduced bit by bit Copy Into the characteristic equation ;
2 . Solution characteristic root : take Characteristic equation Characteristic root Work it out ,
x
=
−
b
±
b
2
−
4
a
c
2
a
x = \cfrac{-b \pm \sqrt{b^2 - 4ac}}{2a}
x=2a−b±b2−4ac
3 . Construct the general solution of recurrence equation :
( 1 ) No double root : structure
c
1
q
1
n
+
c
2
q
2
n
+
⋯
+
c
k
q
k
n
c_1q_1^n + c_2q_2^n + \cdots + c_kq_k^n
c1q1n+c2q2n+⋯+ckqkn Linear combination of forms , This linear combination is the of recursive equations general solution ;
( 2 ) Double root : Refer to the following “ The general solution form under the double root is listed ” Content ;
4 . Find the constant in the general solution :
( 1 ) Substitute the initial values to obtain the equations : Substitute the initial value of the recursive equation into the general solution , obtain
k
k
k individual
k
k
k Finite element equations , adopt Solve the equations , obtain Constants in general solutions ;
( 2 ) Substitute constants to obtain the general solution : Substitute constants into the general solution , You can get the final solution of the recursive equation ;
The general solution form under the double root is listed :
1 . Number of characteristic elements :
q
1
,
q
2
,
⋯
,
q
t
q_1, q_2, \cdots , q_t
q1,q2,⋯,qt Is the characteristic root of recursive equation , Unequal characteristic roots
t
t
t ;
2 . according to Characteristic root Write the items in the general solution
H
i
(
n
)
H_i(n)
Hi(n) : Characteristic root
q
i
q_i
qi , Repeatability
e
i
e_i
ei , among
i
i
i The value is
0
0
0 To
t
t
t; The first
i
i
i The general solution term corresponding to characteristic roots , Write it down as
H
i
(
n
)
H_i(n)
Hi(n) ;
- ( 1 ) form : Coefficient term multiply
q
i
n
q_i^n
qin ;
- ( 2 ) Coefficient term :
- ① Number : Yes
e
i
e_i
ei term ; Number of coefficient terms , Is the repeatability of the characteristic root ;
- ② form : constant multiply
n
n
n
e
i
−
1
n^{e_i-1}
nei−1 , Here you are
e
i
e_i
ei It's a constant ;
- 1 > constant : The constant subscript is from
c
i
1
c_{i1}
ci1 To
c
i
e
i
c_{ie_i}
1
1
1 To
e
i
e_i
ei ;
ciei , The right part of the subscript is
- 2 >
n
n
0
0
0 To
e
i
−
1
e_i - 1
ei−1 ;
n Power of power : The value of power is from
- 3 > Suggested arrangement : constant and The next power , It's best to arrange them from small to large , Constant subscript And
n
n
n The power of Difference between
1
1
1 ;
n Power of power ; Such as :
- 1 > constant : The constant subscript is from
- ① Number : Yes
- ( 3 ) General explanation
i
i
H
i
(
n
)
=
(
c
i
1
+
c
i
2
n
+
⋯
+
c
i
e
i
n
e
i
−
1
)
q
i
n
H_i(n) = (c_{i1} + c_{i2}n + \cdots + c_{ie_i}n^{e_i - 1})q_i^n
Hi(n)=(ci1+ci2n+⋯+cieinei−1)qin
i term :
3 . Write a general solution :
- ( 1 ) Number of general solutions : Number of characteristic elements
t
t
t ;
- ( 2 ) General solution composition : The general solution term corresponding to each characteristic root , Put it all together , Is the complete general solution ;
- ( 3 ) final result :
H
(
n
)
=
∑
i
=
1
t
H
i
(
n
)
H(n) = \sum\limits_{i=1}^tH_i(n)
H(n)=i=1∑tHi(n)
Recurrence equation -> Characteristic equation -> Characteristic root -> general solution -> Substitute the initial value to find the general solution constant
边栏推荐
- CC2530 common registers for crystal oscillator settings
- 大消费企业怎样做数字化转型?
- SVN完全备份svnadmin hotcopy
- The largest matrix (H) in a brush 143 monotone stack 84 histogram
- One brush 142 monotone stack next larger element II (m)
- 27. Input 3 integers and output them in descending order. Pointer method is required.
- [combinatorics] recursive equation (example 1 of recursive equation | list recursive equation)
- CC2530 common registers for ADC single channel conversion
- PHP online confusion encryption tutorial sharing + basically no solution
- One brush 146 force buckle hot question-3 longest substring without repeated characters (m)
猜你喜欢

Arduino esp32: overall framework of lvgl project (I)
智慧之道(知行合一)

Recommendation of good books on learning QT programming

大消费企业怎样做数字化转型?

New features of C 10

What is the pledge pool and how to pledge?

What material is sa537cl2 equivalent to in China? Sa537cl2 corresponding material
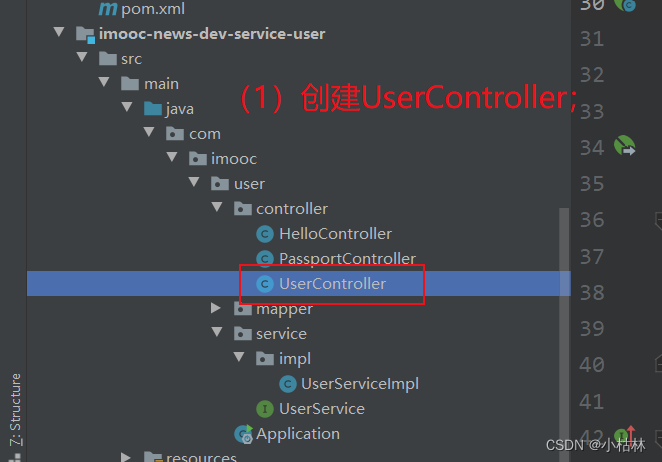
29:第三章:开发通行证服务:12:开发【获得用户账户信息,接口】;(使用VO类包装查到的数据,以符合接口对返回数据的要求)(在多处都会用到的逻辑,在Controller中可以把其抽成一个共用方法)

关于学习Qt编程的好书精品推荐

How do large consumer enterprises make digital transformation?
随机推荐
[combinatorics] recursive equation (characteristic equation and characteristic root | example of characteristic equation | root formula of monadic quadratic equation)
Shentong express expects an annual loss of nearly 1billion
LeetCode 1656. Design ordered flow
Kotlin学习快速入门(7)——扩展的妙用
Meituan side: why does thread crash not cause JVM crash
[combinatorial mathematics] counting model, common combinatorial numbers and combinatorial identities**
新库上线 | CnOpenData中国保险机构网点全集数据
建立自己的网站(23)
PHP online confusion encryption tutorial sharing + basically no solution
Leetcode: lucky number in matrix
RF Analyze Demo搭建 Step by Step
Cross border e-commerce: advantages of foreign trade enterprises in overseas social media marketing
數據分析必備的能力
Simple configuration of postfix server
vs code 插件 koroFileHeader
Define a structure fraction to represent a fraction, which is used to represent fractions such as 2/3 and 5/6
[Jianzhi offer] 58 - ii Rotate string left
大消费企业怎样做数字化转型?
What is your income level in the country?
One brush 149 force deduction hot question-10 regular expression matching (H)
