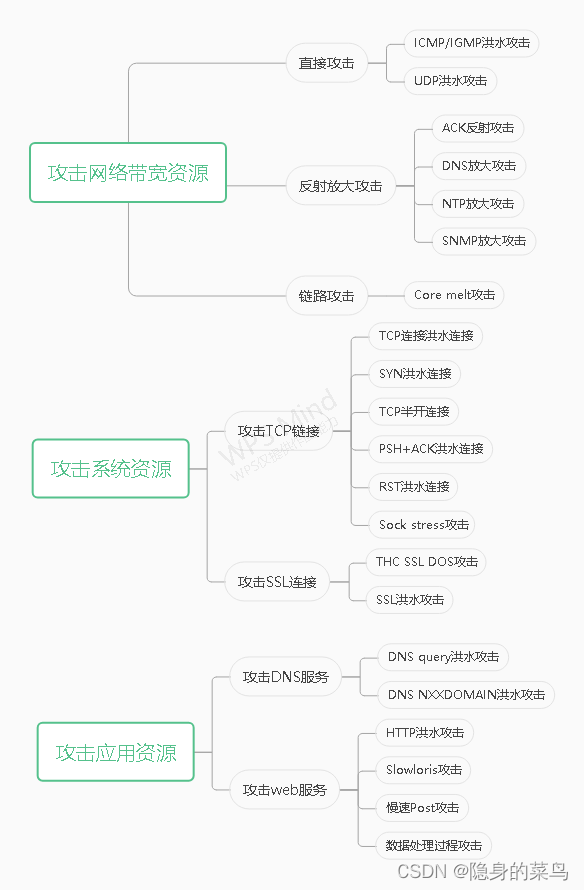
当前位置:网站首页>Codeforces Round #811 (Div. 3)
Codeforces Round #811 (Div. 3)
2022-08-04 21:08:00 【Vegetable newbie】
Codeforces Round #811 (Div. 3)
D.Color with Occurrences
题意:
给你一个长度为 ∣ t ∣ |t| ∣t∣的母串 t t t,给你 n n n个子串,如果子串和母串的某个子串一样,你可以将其染成红色,问最小染色次数以及方案。
思路:
比赛的时候一开始想直接模拟,然后发现虽然时间复杂度够,但是情况太多。赛后发现可以把问题转化下。
我们可以先把母串每个字母可以向右匹配的最大长度记录下来,然后从左往右贪心的遍历:假如母串第 1 1 1个字母能匹配到第 e n d end end位置,那么下一次我们应该从第 2 2 2~ m i n ( e n d + 1 , ∣ t ∣ ) min(end + 1, |t|) min(end+1,∣t∣)里面找能匹配更加靠后的位置,一直找到最后一个字母为止。
注意:如果子串中有和母串一模一样的,就可以直接输出答案。
后面贪心的过程,有一段小模拟,还是要多写代码多总结,这种题才能又快有准确写对。
代码
const int N = 110;
string t;
int n;
string s[15];
int r[N], ans[N];//r[i]存的是最右能到达哪
vector<PII>res;
void solve()
{
res.clear();
memset(r, -1, sizeof r);
t = rd();read(n);int szt = sz(t);
for(int i = 1; i <= n; i ++ ){
s[i] = rd();
}
for(int i = 0; i < szt; i ++ ){
for(int j = 1; j <= n; j ++ ){
if(s[j] == t){
printf("%d\n%d %d\n",1, j, 1);
return;
}
int szs = sz(s[j]);
if(t.substr(i, szs) == s[j]){
if(i + szs - 1 > r[i]){
r[i] = i + szs - 1;
ans[i] = j;
}
}
}
}
res.pb({
ans[0], 0});
int start = 0, ends = r[0] + 1;
while(true){
int x = -1, y = -1;
int maxlen = -1;
for(int i = start; i <= min(szt, ends); i ++ ){
if(r[i] > maxlen){
maxlen = r[i];
x = i, y = ans[i];
}
}
if(x == -1 || start == x){
puts("-1");
return;
}
start = x;
ends = x + sz(s[y]);
res.push_back({
y, x});
if(ends == szt) break;
}
writeln(res.size());
for(auto it : res){
printf("%d %d\n",it.fi,it.se + 1);
}
return;
}
E. Add Modulo 10
题意:
给你一个数组 a a a,你可以对里面的元素进行以下操作
- a [ i ] = a [ i ] + a [ i ] % 10 a[i] = a[i] + a[i] \% 10 a[i]=a[i]+a[i]%10
问你能否将数组变成一样。
思路:
这题规律非常明显了,对于大部分数而言,个位数往后都是 2 、 4 、 8 、 6 2 、4、8、6 2、4、8、6循环,周期长度是 20 20 20。然后可以写一串数字进行分析,容易发现,以2为个位转化为以 2 、 4 、 8 、 6 2、4、8、6 2、4、8、6为个位的数分别可以在原有的数上加上 { 0 、 2 、 14 、 6 } + k ∗ 20 ( k ⩾ 0 ) \{0、2、14、6\} + k * 20 (k \geqslant 0) { 0、2、14、6}+k∗20(k⩾0),其余的数同理,(非常愚蠢的做法,几乎不要动脑子)。
注意:个位数为 5 5 5的和个位数为 0 0 0的要特判一下
代码:
const int N = 200010;
int a[N];
int n;
map<int,int>mp;
void solve()
{
mp.clear();
read(n);
for(int i = 1; i <= n; i ++ ){
read(a[i]);
if(a[i] % 10 == 5) mp[a[i] + 5] ++;
else if(a[i] % 10 == 0) mp[a[i]] ++;
}
if(mp.size() >= 2){
puts("No");
return;
}
if(mp.size() == 1){
for(auto it : mp){
if(it.second != n){
puts("No");
return;
}
}
puts("Yes");
return;
}
for(int i = 1; i <= n; i ++ ){
while(a[i] % 2 == 1){
a[i] = a[i] + (a[i] % 10);
}
}
sort(a + 1, a + 1 + n);
cout << endl;
for(int i = 2; i <= n; i ++ ){
int m1 = a[i] % 10, m2 = a[i - 1] % 10;//从m2变化到m1
int cha = a[i] - a[i - 1];
if(m2 == 2){
if(m1 == 2 && cha % 20 != 0){
puts("No");
return;
}else if(m1 == 4 && cha % 20 != 2){
puts("No");
return;
}else if(m1 == 6 && cha % 20 != 14){
puts("No");
return;
}else if(m1 == 8 && cha % 20 != 6){
puts("No");
return;
}
}
if(m2 == 4){
if(m1 == 2 && cha % 20 != 18){
puts("No");
return;
}else if(m1 == 4 && cha % 20 != 0){
puts("No");
return;
}else if(m1 == 6 && cha % 20 != 12){
puts("No");
return;
}else if(m1 == 8 && cha % 20 != 4){
puts("No");
return;
}
}
if(m2 == 6){
if(m1 == 2 && cha % 20 != 6){
puts("No");
return;
}else if(m1 == 4 && cha % 20 != 8){
puts("No");
return;
}else if(m1 == 6 && cha % 20 != 0){
puts("No");
return;
}else if(m1 == 8 && cha % 20 != 12){
puts("No");
return;
}
}
if(m2 == 8){
if(m1 == 2 && cha % 20 != 14){
puts("No");
return;
}else if(m1 == 4 && cha % 20 != 16){
puts("No");
return;
}else if(m1 == 6 && cha % 20 != 8){
puts("No");
return;
}else if(m1 == 8 && cha % 20 != 0){
puts("No");
return;
}
}
}
puts("Yes");
return;
}
F. Build a Tree and That Is It
题意:
给你 n n n个点和 d 12 、 d 23 、 d 13 d_{12}、d_{23}、d_{13} d12、d23、d13,让你构造一张无向图。
思路:
分两种情况讨论:链式和分叉式,链式是一种特殊的分叉式。
如果存在 d 12 、 d 23 、 d 13 d_{12}、d_{23}、d_{13} d12、d23、d13其中两个和等于另外一个和,可以采用链式构造,例如 d 12 + d 23 = d 13 d_{12} + d_{23} = d_{13} d12+d23=d13,可以构造成: 1 , x , x , x , 2 , x , x , x , 3 1, x, x, x, 2,x,x,x, 3 1,x,x,x,2,x,x,x,3。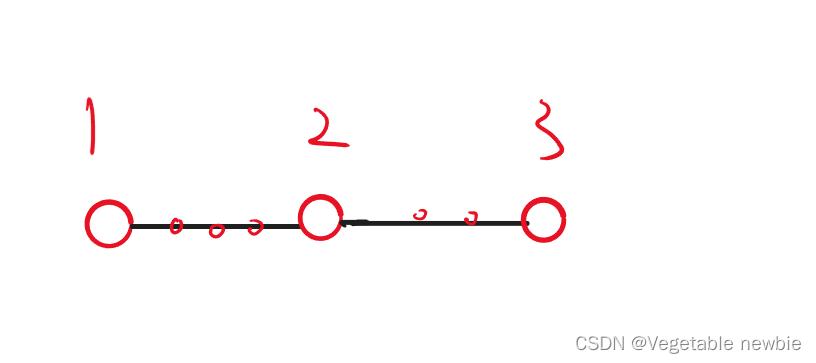
如果不满足上述条件可以构造成分叉式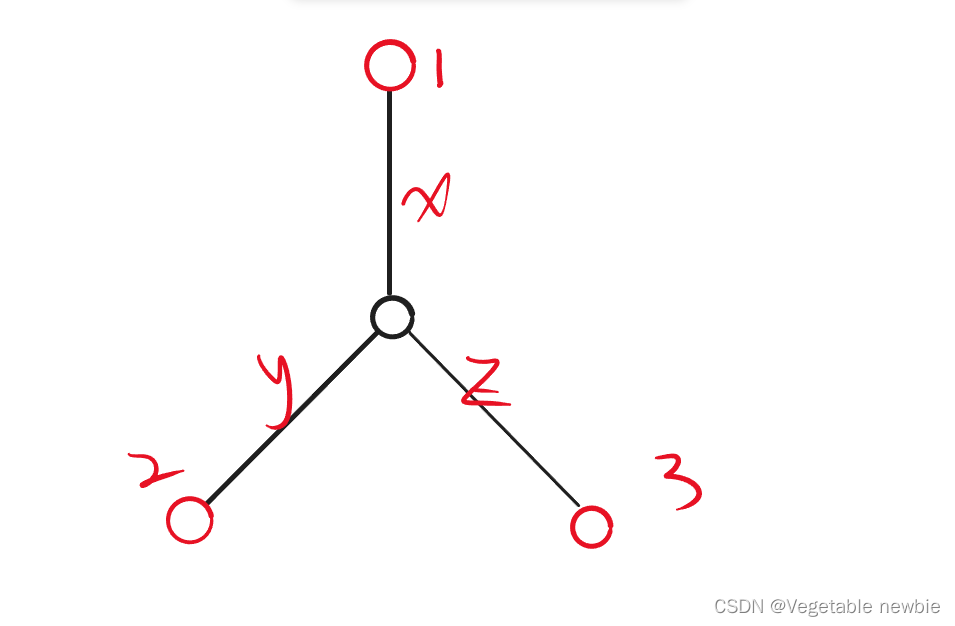
可以根据方程组
{ x + y = d 12 x + z = d 13 y + z = d 12 \begin{cases} x + y = d_{12}\\ x + z = d_{13} \\ y + z = d_{12} \end{cases} ⎩⎨⎧x+y=d12x+z=d13y+z=d12
解出 :
{ x = d 13 + d 12 − d 23 2 y = d 12 + d 23 − d 13 2 z = d 23 + d 13 − d 12 2 \begin{cases}x = \frac{d_{13} + d_{12} - d_{23}}{2}\\ y = \frac{d_{12} + d_{23} - d_{13}}{2}\\ z = \frac{d_{23} + d_{13} - d_{12}}{2}\end{cases} ⎩⎨⎧x=2d13+d12−d23y=2d12+d23−d13z=2d23+d13−d12
要保证分子都是大于 0 0 0的偶数,如果分子都是 0 0 0那么就是链式的,已经讨论过了。
代码
#include <bits/stdc++.h>
#define PII pair<int,int>
#define LL long long
#define fi first
#define se second
#define debug(a) cout<<#a<<"="<<a<<endl;
#define all(x) (x).begin(),(x).end()
#define pb push_back
#define sz(x) (int)x.size()
using namespace std;
inline string rd()
{
string str="";
char ch=getchar();
while(ch==' ' || ch=='\n' || ch=='\r')
{
ch=getchar();
}
while(ch!=' ' && ch!='\n' && ch!='\r')
{
str+=ch;
ch=getchar();
}
return str;
}
inline void print(string s)
{
for(int i=0; s[i]!='\0'; i++) putchar(s[i]);
}
template <typename T> void read(T &t) {
t=0; char ch=getchar(); int f=1;
while (ch<'0'||ch>'9') {
if (ch=='-') f=-1; ch=getchar(); }
do {
(t*=10)+=ch-'0'; ch=getchar(); } while ('0'<=ch&&ch<='9'); t*=f;
}
template <typename T> void write(T t) {
if (t<0) {
putchar('-'); write(-t); return; }
if (t>9) write(t/10);
putchar('0'+t%10);
}
template <typename T> void writeln(T t) {
write(t); puts(""); }
const int N = 200010;
int n, d12, d13, d23;
bool st[N];
vector<PII>ans;
void print(vector<PII>ans){
puts("YES");
for(auto it : ans){
printf("%d %d\n",it.fi, it.se);
}
return;
}
void solve()
{
ans.clear();
read(n);read(d12);read(d23);read(d13);
//链式:
int idx = 4;
int pre = 1;
if(d12 + d23 == d13){
bool f = 1;
for(int i = 1; i <= d12 - 1; i ++ ){
ans.pb({
pre, idx});
pre = idx;
idx ++;
}
if(idx - 1 > n){
f = 0;
}
ans.pb({
pre, 2});
pre = 2;
for(int i = 1; i <= d23 - 1 && f; i ++ ){
ans.pb({
pre, idx});
pre = idx;
idx ++;
}
if(idx - 1 > n){
f = 0;
}
ans.pb({
pre, 3});
for(int i = idx; i <= n && f; i ++ ){
ans.pb({
1, i});
}
if(f){
print(ans);
return;
}
}
idx = 4;
pre = 1;
if(d13 + d23 == d12){
bool f = 1;
for(int i = 1; i <= d13 - 1; i ++ ){
ans.pb({
pre, idx});
pre = idx;
idx ++;
}
if(idx - 1 > n){
f = 0;
}
ans.pb({
pre, 3});
pre = 3;
for(int i = 1; i <= d23 - 1 && f; i ++ ){
ans.pb({
pre, idx});
pre = idx;
idx ++;
}
if(idx - 1 > n){
f = 0;
}
ans.pb({
pre, 2});
for(int i = idx; i <= n && f; i ++ ){
ans.pb({
1, i});
}
if(f){
print(ans);
return;
}
}
idx = 4;
pre = 2;
if(d12 + d13 == d23){
bool f = 1;
for(int i = 1; i <= d12 - 1; i ++ ){
ans.pb({
pre, idx});
pre = idx;
idx ++;
}
if(idx - 1 > n){
f = 0;
}
ans.pb({
pre, 1});
pre = 1;
for(int i = 1; i <= d13 - 1 && f; i ++ ){
ans.pb({
pre, idx});
pre = idx;
idx ++;
}
if(idx - 1 > n){
f = 0;
}
ans.pb({
pre, 3});
for(int i = idx; i <= n && f; i ++ ){
ans.pb({
1, i});
}
if(f){
print(ans);
return;
}
}
//分叉式:
if(d12 + d23 <= d13 || d12 + d13 <= d23 || d23 + d13 <= d12){
puts("NO");
return;
}
if((d12 + d23 - d13) % 2 || (d23 + d13 - d12) % 2 || (d13 + d12 - d23) % 2){
puts("NO");
return;
}
int x = (d12 + d13 - d23) / 2, y = (d23 + d12 - d13) / 2, z = (d23 + d13 - d12) / 2;
if(n - 5 + 1 < x - 1 + y - 1 + z - 1 ){
puts("NO");
return;
}
idx = 5;
pre = 1;
for(int i = 1; i <= x - 1; i ++ ){
ans.pb({
idx, pre});
pre = idx;
idx ++;
}
ans.pb({
pre, 4});
pre = 4;
for(int i =1; i <= y - 1; i ++ ){
ans.pb({
idx, pre});
pre = idx;
idx ++;
}
ans.pb({
pre, 2});
pre = 4;
for(int i = 1; i <= z - 1; i ++ ){
ans.pb({
idx, pre});
pre = idx;
idx ++;
}
ans.pb({
pre, 3});
for(int i = idx; i <= n; i ++ ){
ans.pb({
i, 1});
}
print(ans);
}
int main()
{
int test = 1;
scanf("%d",&test);
while(test -- )
{
solve();
}
return 0;
}
G. Path Prefixes
题意:
给你一个以 1 1 1为根的树,有 n n n个节点, n − 1 n - 1 n−1条边,每条边有两个属性值 a i a_i ai, b i b_i bi,对于每一个节点 i i i求:
从根节点到 i i i节点的路径中, b i b_i bi的前缀(小于等于从 1 1 1到 i i i中路径上所有 a i a_i ai的和)的个数。
思路:
从根节点开始对每一个节点进行深度优先遍历,并记录 a i 、 b i a_i、b_i ai、bi的前缀和,并对所有的 ∑ a i \sum{a_i} ∑ai,二分 b i b_i bi的前缀个数。
代码:
#include <bits/stdc++.h>
#define PII pair<int,int>
#define LL long long
#define fi first
#define se second
#define debug(a) cout<<#a<<"="<<a<<endl;
#define all(x) (x).begin(),(x).end()
#define pb push_back
#define sz(x) (int)x.size()
using namespace std;
const int N = 200010, M = 400010;
inline string rd()
{
string str="";
char ch=getchar();
while(ch==' ' || ch=='\n' || ch=='\r')
{
ch=getchar();
}
while(ch!=' ' && ch!='\n' && ch!='\r')
{
str+=ch;
ch=getchar();
}
return str;
}
inline void print(string s)
{
for(int i=0; s[i]!='\0'; i++) putchar(s[i]);
}
template <typename T> void read(T &t) {
t=0; char ch=getchar(); int f=1;
while (ch<'0'||ch>'9') {
if (ch=='-') f=-1; ch=getchar(); }
do {
(t*=10)+=ch-'0'; ch=getchar(); } while ('0'<=ch&&ch<='9'); t*=f;
}
template <typename T> void write(T t) {
if (t<0) {
putchar('-'); write(-t); return; }
if (t>9) write(t/10);
putchar('0'+t%10);
}
template <typename T> void writeln(T t) {
write(t); puts(""); }
int e[M], A[M], h[N], ne[N], B[M], idx, n;
LL suma[M], sumb[M], ans[N];
bool st[N];
void add(int a, int b, int wa, int wb){
A[idx] = wa, B[idx] = wb, e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}
void dfs(int u, int cnt){
st[u] = true;
for(int i = h[u]; ~i; i = ne[i]){
int j = e[i];
suma[cnt + 1] = suma[cnt] + A[i], sumb[cnt + 1] = sumb[cnt] + B[i];
cnt ++;
int l = 0, r = cnt;
while(l < r){
int mid = l + r + 1 >> 1;
if(sumb[mid] <= suma[cnt]) l = mid;
else r = mid - 1;
}
ans[j] = l;
if(!st[j]) dfs(j, cnt);
cnt --;
}
}
void solve()
{
read(n);
idx = 0;
for(int i = 1; i <= n; i ++ ){
h[i] = -1;
st[i] = false;
}
for(int i = 2; i <= n; i ++ ){
int x, wa, wb;
read(x);read(wa);read(wb);
add(x, i, wa, wb);
}
dfs(1, 0);
for(int i = 2; i <= n; i ++ ){
write(ans[i]);
putchar(' ');
}
puts("");
}
int main()
{
int test = 1;
scanf("%d",&test);
while(test -- )
{
solve();
}
return 0;
}
边栏推荐
猜你喜欢
随机推荐
PyTorch Geometric (PyG) 安装教程
visual studio 2015 warning MSB3246
JWT主动校验Token是否过期
3、IO流之字节流和字符流
stm32mp157系统移植 | 移植ST官方5.10内核到小熊派开发板
【PCBA方案设计】握力计方案
该如何训练好深度学习模型?
【2022杭电多校5 1003 Slipper】多个超级源点+最短路
帝国CMS仿核弹头H5小游戏模板/92game帝国CMS内核仿游戏网整站源码
数据仓库(1)什么是数据仓库,数仓有什么特点
大势所趋之下的nft拍卖,未来艺术品的新赋能
Three ways to set a specific device UWP XAML view
密码学系列之:PEM和PKCS7,PKCS8,PKCS12
visual studio 2015 warning MSB3246
命名路由、组件中name的作用
【2022牛客多校5 A题 Don‘t Starve】DP
js的new Function()常用方法
Spss-一元回归实操
文章复现:超分辨率网络-VDSR
DSPE-PEG-Aldehyde, DSPE-PEG-CHO, Phospholipid-Polyethylene Glycol-Aldehyde A hydrophobic 18-carbon phospholipid