当前位置:网站首页>Day35 LeetCode
Day35 LeetCode
2022-08-02 20:03:00 【太阳在坠落】
1. 最近最少使用的缓存
运用所掌握的数据结构,设计和实现一个 LRU (Least Recently Used,最近最少使用) 缓存机制 。
实现 LRUCache 类:
- LRUCache(int capacity) 以正整数作为容量 capacity 初始化 LRU 缓存 。
- int get(int key)如果关键字 key 存在于缓存中,则返回关键字的值,否则返回 -1 。
- void put(int key, int value)如果关键字已经存在,则变更其数据值;如果关键字不存在,则插入该组「关键字-值」。当缓存容量达到上限时,它应该在写入新数据之前删除最久未使用的数据值,从而为新的数据值留出空间。
分析:
使用的哈希表+双端队列来实现。哈希表用来存储键值对并来判断key是否已经存在,双端队列用来维护每个key出现的顺序,最久未使用的数据值一直在队尾。
class LRUCache {
HashMap<Integer, Integer> map;
Deque<Integer> deque;
int capacity;
public LRUCache(int capacity) {
this.capacity = capacity;
map = new HashMap<>();
deque = new LinkedList<>();
}
public int get(int key) {
if (map.containsKey(key)) {
deque.remove(key);
deque.addFirst(key);
return map.get(key);
}
return -1;
}
public void put(int key, int value) {
if (map.containsKey(key)){
deque.remove(key);
deque.addFirst(key);
map.put(key, value);
}else {
if (deque.size() >= capacity){
int k = deque.pollLast();
map.remove(k);
}
map.put(key, value);
deque.addFirst(key);
}
}
}
2. 插入、随机访问和删除都是O(1)的容器
设计一个支持在平均 时间复杂度 O(1) 下,执行以下操作的数据结构:
- insert(val):当元素 val 不存在时返回 true ,并向集合中插入该项,否则返回 false 。
- remove(val):当元素 val 存在时返回 true ,并从集合中移除该项,否则返回 false 。
- getRandom:随机返回现有集合中的一项。每个元素应该有 相同的概率 被返回。
分析:
哈希表+List集合。List用来存储当前结构中的值,当执行insert(val)时先在哈希表中查找是否有该val,有则返回false,没有则把val插入到list中去,并在哈希表中记录val和它的位置。执行remove时,也是先去哈希表中查找是否有该val,如果有则先获取当前list最后面的值last,再把last的值插入到原来val所在的位置,并在哈希表中更新这些内容。getRandom实现比较简单,直接生成一个随机数在[0,List.size())区间,然后返回该下标的值。
class RandomizedSet {
HashMap<Integer, Integer> set;
List<Integer> list;
/** Initialize your data structure here. */
public RandomizedSet() {
set = new HashMap<>();
list = new ArrayList<>();
}
/** Inserts a value to the set. Returns true if the set did not already contain the specified element. */
public boolean insert(int val) {
if (set.containsKey(val)) return false;
set.put(val, list.size());
list.add(val);
return true;
}
/** Removes a value from the set. Returns true if the set contained the specified element. */
public boolean remove(int val) {
if (set.containsKey(val)){
int idx = set.get(val);
int value = list.get(list.size()-1);
list.set(idx, value);
set.put(value, idx);
list.remove(list.size()-1);
set.remove(val);
return true;
}
return false;
}
/** Get a random element from the set. */
public int getRandom() {
Random r = new Random();
int idx = r.nextInt(list.size());
return list.get(idx);
}
}
3. 排序的循环链表
给定循环单调非递减列表中的一个点,写一个函数向这个列表中插入一个新元素 insertVal ,使这个列表仍然是循环升序的。
给定的可以是这个列表中任意一个顶点的指针,并不一定是这个列表中最小元素的指针。
如果有多个满足条件的插入位置,可以选择任意一个位置插入新的值,插入后整个列表仍然保持有序。
如果列表为空(给定的节点是 null),需要创建一个循环有序列表并返回这个节点。否则。请返回原先给定的节点。
分析:
如果循环链表为空,则插入一个新节点并将新节点的 next 指针指向自身,插入新节点之后得到只有一个节点的循环链表,该循环链表一定是有序的,将插入的新节点作为新的头节点返回。
如果循环链表的头节点的next 指针指向自身,则循环链表中只有一个节点,在头节点之后插入新节点,将头节点的next 指针指向新节点,将新节点的next 指针指向头节点,此时循环链表中有两个节点且一定是有序的,返回头节点。
如果循环链表中的节点数大于 1,则需要从头节点开始遍历循环链表,寻找插入新节点的位置,使得插入新节点之后的循环链表仍然保持有序。
用 cur 和next 分别表示当前节点和下一个节点,初始时cur 位于head,next 位于head 的下一个节点,由于链表中的节点数大于 1,因此curr.next=next。遍历过程中,判断值为insertVal 的新节点是否可以在curr 和 next 之间插入,如果符合插入要求则在 curr 和next 之间插入新节点,否则将 curr 和 next 同时向后移动,直到找到插入新节点的位置或者遍历完循环链表中的所有节点。要注意insertVal小于全部节点值和大于全部节点值时的情况,还有所有值都相等时的情况。
class Solution {
public Node insert(Node head, int insertVal) {
if (head == null) {
Node node = new Node(insertVal);
node.next = node;
return node;
}
if (head.next == head){
Node node = new Node(insertVal);
node.next = head;
head.next = node;
return head;
}
Node cur = head;
Node next = head.next;
Node node = new Node(insertVal);
while (next != head){
if (insertVal>= cur.val && insertVal<=next.val){
cur.next = node;
node.next = next;
return head;
}
if (cur.val > next.val){
if (insertVal> cur.val || insertVal< next.val) {
cur.next = node;
node.next = next;
return head;
}
}
cur = cur.next;
next = next.next;
}
cur.next = node;
node.next = next;
return head;
}
}
4. 展平多级双向链表
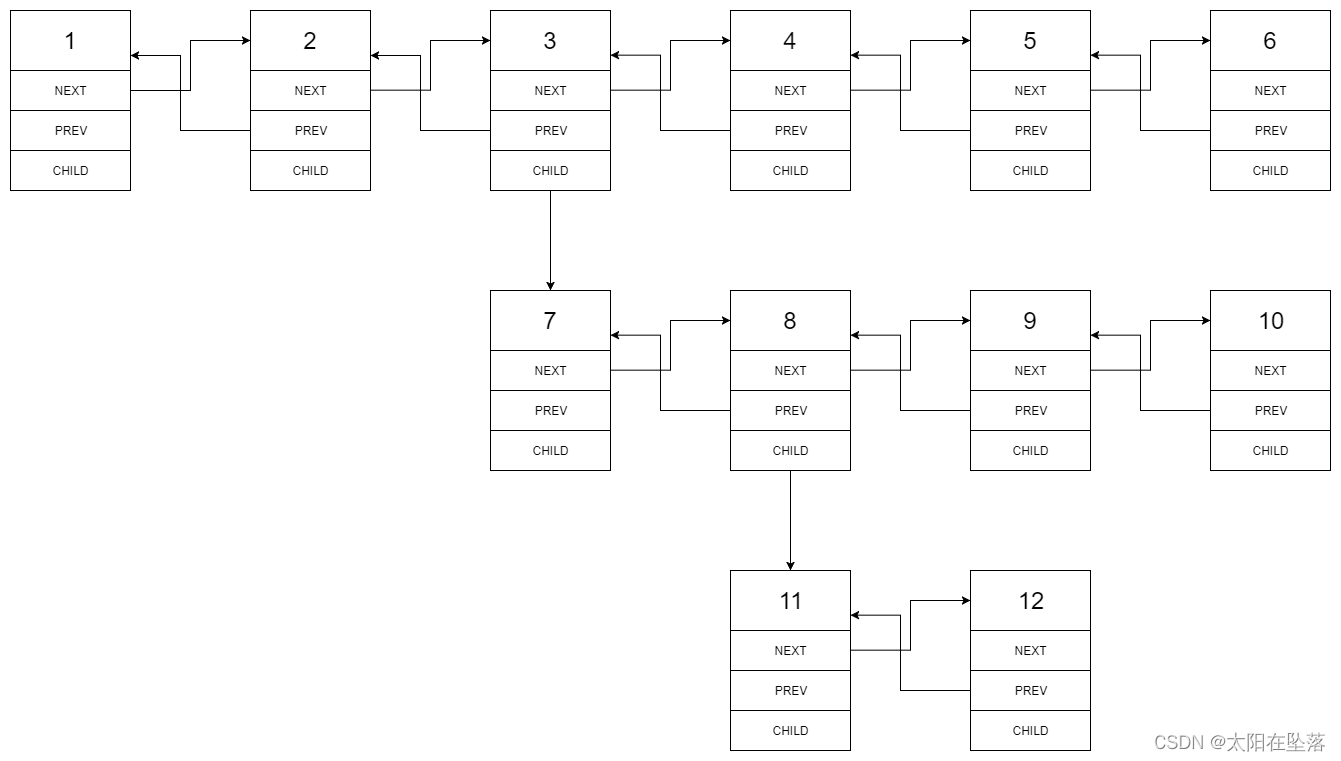
多级双向链表中,除了指向下一个节点和前一个节点指针之外,它还有一个子链表指针,可能指向单独的双向链表。这些子列表也可能会有一个或多个自己的子项,依此类推,生成多级数据结构,如下面的示例所示。
给定位于列表第一级的头节点,请扁平化列表,即将这样的多级双向链表展平成普通的双向链表,使所有结点出现在单级双链表中。

分析:
DFS。当遍历到某个节点node 时,如果它的 child 成员不为空,那么我们需要将child 指向的链表结构进行扁平化,并且插入node 与node 的下一个节点之间。
因此,我们在遇到 child 成员不为空的节点时,就要先去处理 child 指向的链表结构,这就是一个「深度优先搜索」的过程。当我们完成了对child 指向的链表结构的扁平化之后,就可以「回溯」到 node 节点。
为了能够将扁平化的链表插入node 与 node 的下一个节点之间,我们需要知道扁平化的链表的最后一个节点last,随后进行如下的三步操作:
- 将 node 与 node 的下一个节点next 断开;
- 将node 与 child 相连;
- 将 last 与 next 相连。
class Solution {
public Node flatten(Node head) {
dfs(head);
return head;
}
public Node dfs(Node node) {
Node cur = node;
// 记录链表的最后一个节点
Node last = null;
while (cur != null) {
Node next = cur.next;
// 如果有子节点,那么首先处理子节点
if (cur.child != null) {
Node childLast = dfs(cur.child);
next = cur.next;
// 将 node 与 child 相连
cur.next = cur.child;
cur.child.prev = cur;
// 如果 next 不为空,就将 last 与 next 相连
if (next != null) {
childLast.next = next;
next.prev = childLast;
}
// 将 child 置为空
cur.child = null;
last = childLast;
} else {
last = cur;
}
cur = next;
}
return last;
}
}
5. 设计循环队列
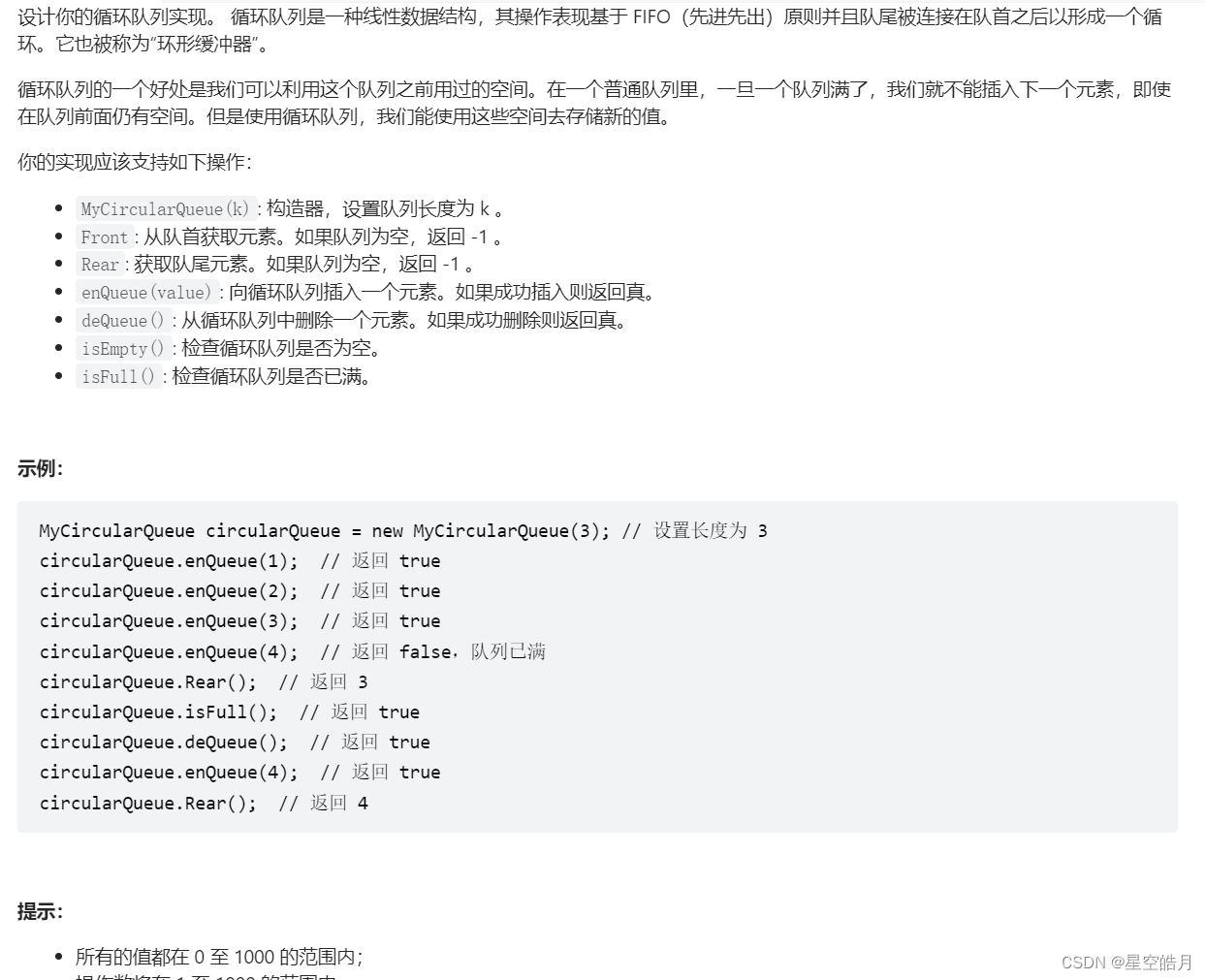
设计你的循环队列实现。 循环队列是一种线性数据结构,其操作表现基于 FIFO(先进先出)原则并且队尾被连接在队首之后以形成一个循环。它也被称为“环形缓冲器”。
循环队列的一个好处是我们可以利用这个队列之前用过的空间。在一个普通队列里,一旦一个队列满了,我们就不能插入下一个元素,即使在队列前面仍有空间。但是使用循环队列,我们能使用这些空间去存储新的值。
你的实现应该支持如下操作:
- MyCircularQueue(k): 构造器,设置队列长度为 k 。
- Front: 从队首获取元素。如果队列为空,返回 -1 。
- Rear: 获取队尾元素。如果队列为空,返回 -1 。
- enQueue(value): 向循环队列插入一个元素。如果成功插入则返回真。
- deQueue(): 从循环队列中删除一个元素。如果成功删除则返回真。
- isEmpty(): 检查循环队列是否为空。
- isFull(): 检查循环队列是否已满。
分析:
使用Deque类来实现。
class MyCircularQueue {
Deque<Integer> queue;
int k;
public MyCircularQueue(int k) {
queue = new LinkedList<>();
this.k = k;
}
public boolean enQueue(int value) {
if (queue.size() >= k) return false;
queue.addLast(value);
return true;
}
public boolean deQueue() {
if (queue.size() == 0) return false;
queue.pollFirst();
return true;
}
public int Front() {
return queue.isEmpty()?-1:queue.getFirst();
}
public int Rear() {
return queue.isEmpty()?-1:queue.getLast();
}
public boolean isEmpty() {
return queue.isEmpty();
}
public boolean isFull() {
return queue.size() == k;
}
}
边栏推荐
猜你喜欢

What is a Field Service Management System (FSM)?what is the benefit?

数字孪生助力智慧城市可视化建设
The time series database has been developed for 5 years. What problem does it need to solve?

信息学奥赛一本通(1259:【例9.3】求最长不下降序列)

谷歌竞价机器学习如何去理解?

J9 digital theory: the Internet across chain bridge has what effect?
LeetCode:622. 设计循环队列【模拟循环队列】

LM小型可编程控制器软件(基于CoDeSys)笔记二十五:plc的数据存储区(数字量输入通道部分)
Shell: conditional statements

即时通讯开发移动端网络短连接的优化手段
随机推荐
【StoneDB性能相关工具】内存监控
模板的进阶
.NET性能优化-你应该为集合类型设置初始大小
J9 Digital Currency Theory: Identifying Web3's New Scarcity: Open Source Developers
Introduction of uncommon interfaces of openlayers
SQL Server安装教程
ABAP语法小复习
The so-called fighting skill again gao also afraid of the chopper - partition, depots, table, and the merits of the distributed
Redis集群配置
新增指令 v-memo
V - memo new instructions
The time series database has been developed for 5 years. What problem does it need to solve?
Thread线程类基本使用(上)
ALV概念讲解
Helm基础知识
GNN教程:图神经网络基础知识!
成为黑客不得不学的语言,看完觉得你们还可吗?
什么是乙二醇二乙酸酯(EGDA)?
KDD 2022 | 深度图神经网络中的特征过相关:一个新视角
LeetCode - 105. 从前序与中序遍历序列构造二叉树;023.合并K个升序链表
