Missile interception -- UPC winter vacation training match

subject

Background

after 11 Years of hiding one's strength and cultivating one's obscurity , A country has developed a new missile interception system , Any missile whose distance from it does not exceed its working radius can be successfully intercepted by it . When the working radius is 0 when , It can intercept missiles in exactly the same position . But the missile interception system also has such defects ： Each system can only set the working radius once a day . And the use cost of the day , Is the sum of the squares of the working radii of all systems .

One day , The radar caught the enemy's missiles coming . Because the system is still in the experimental stage , So only two systems are working . If the current requirement is to intercept all missiles , Please calculate the minimum use cost of this day .

Input

The first line contains 4 It's an integer x1、y1、x2、y2, Every two integers are separated by a space , The coordinates of the two missile interception systems are (x1,y1)、(x2,y2).
The second line contains 1 It's an integer N(1≤N≤100000), Express N Missiles . Next N That's ok , Two integers per line x、y, Separated by a space , Represents the coordinates of a missile (x,y). The coordinates of different missiles may be the same .

Output

There is only one line of output , Contains an integer , That is, the minimum use cost of the day .

The sample input

0 0 10 0
2
-3 3
10 0

Sample output

18

Tips and data range limitations

Two points (x1,y1)、(x2,y2) The square of the distance between is (x1−x2)2+(y1−y2)2.
The working radius of the two systems r1、r2 Sum of squares of , Refer to r1、r2 Take the squares respectively and then sum , namely r12+r22.

about 100% The data of ,1≤N≤100000, And the absolute value of all coordinate components does not exceed 1000. 

---

Thought analysis

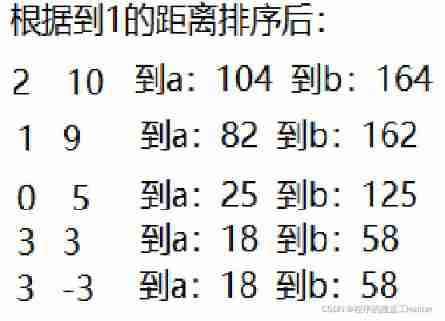
Wrong thinking ： At the beginning of this question, I thought that this missile was intercepted by the nearest interception system , But the result is WA. Ah , Still too simple . If you follow my idea , Later, I came up with a good example , On a number axis ,0 and 5 Is the location of the interception system , Now if it's in -5 and 4 There is a missile at , Obviously, our previous thinking is wrong , This only needs to be used in 0 The interception system of the location is ok .

The right way of thinking ： The correct way to do this is to follow 1 Sort by the distance of , Then find a suitable dividing point i Make part of it intercepted by the first interception system , The other part is intercepted by the second interception system . In this way, we can find the minimum sum of squares

I don't say much nonsense , Code up  

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll N=1e5+10;
ll xa,xb,ya,yb;
struct node{
	ll x,y;
	ll disa,disb;
}a[N];
ll da,db;
ll n;
bool cmp(node c,node d){
	return c.disa>d.disa;
}
int main()
{
	cin>>xa>>ya>>xb>>yb;// Enter the location coordinates of the two interception systems  
	cin>>n;// Enter the number of missiles  
	for(ll i=1;i<=n;i++){
		cin>>a[i].x>>a[i].y;// Enter the first i Position coordinates of missiles  
		a[i].disa=(a[i].x-xa)*(a[i].x-xa)+(a[i].y-ya)*(a[i].y-ya);// Calculate to a The square of the distance  
		a[i].disb=(a[i].x-xb)*(a[i].x-xb)+(a[i].y-yb)*(a[i].y-yb);// Calculate to b The square of the distance  
	}
	sort(a+1,a+1+n,cmp);// Sort according to the position from the first interception system  
	ll ans=INT_MAX;// Define a variable to store the answer , Assign the initial value to infinity  
	ll r2=0;// Define a variable to record the radius set by the second interception system  
	for(ll i=1;i<=n+1;i++){
		ll r1=a[i].disa;// Radius of the first interception system  
		r2=max(r2,a[i-1].disb);// Find the interception radius of the second interception system  
		ans=min(r1+r2,ans);// Find the most suitable decomposition point is the sum of the squares of the minimum distance  
	}
	cout<<ans;
	return 0;
}

  Examples of operation process