Why is quicksort so fast?

5 Line code , Can let wechat small program on the shelf to their own APP in | Register and send it to Dajiang 、 Huawei 、 Cherry keyboard ！>>>

Quick sort

First, choose a benchmark pivot, And then go through the array ,

• The less than pivot All moved to pivot Left side ,
• The greater than pivot All moved to pivot To the right of .

thus , This pivot That's where it's located , That is to say, it's arranged 1 Elements .

Then on pivot On the left The order of the number of ,
Yes pivot On the right The order of the number of ,
It's done. .

How about the left and right ？

answer ： Same method .

So the express line is also used Divide and conquer method Thought .

「 branch 」

Select a pivot, The problem is divided into

• pivot On the left
• pivot On the right

These two questions .

「 cure 」

It's the method described at the beginning , Until within each interval There is no element or only one element left You can go back to .

「 close 」

Put together, naturally it is .

But how to choose this pivot？

Take the middle one ？

Take the first one ？

Take the last one ？

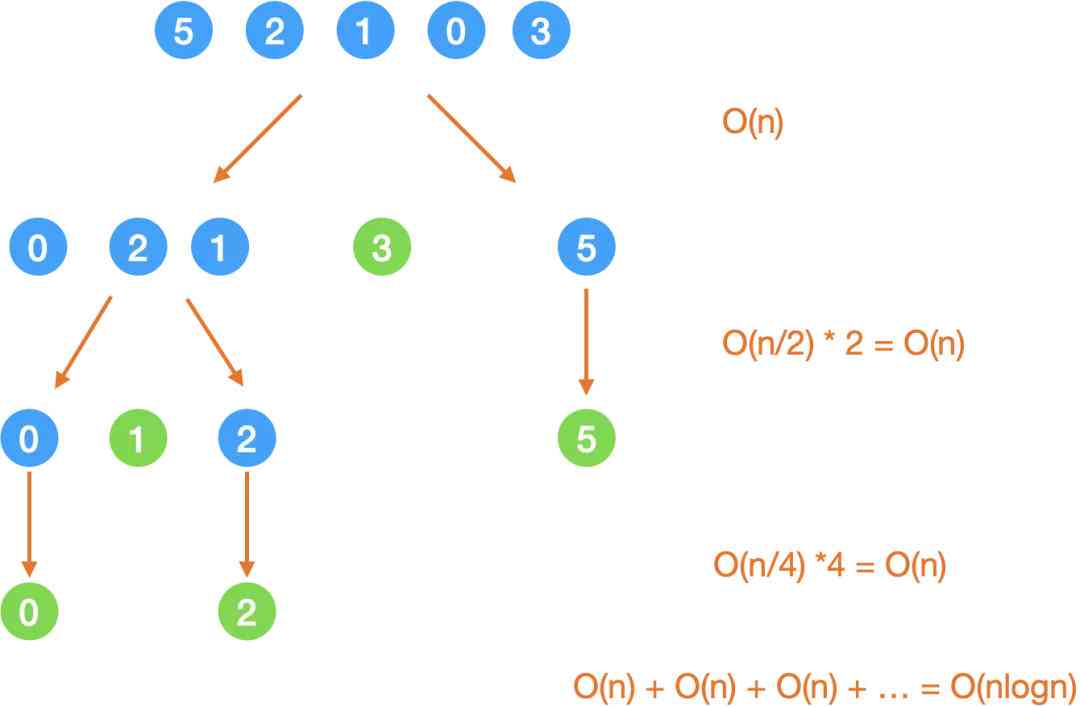
for instance ：{5, 2, 1, 0, 3}.

Take the last one , Namely 3.

And then we need to get rid of 3 The other number is divided into 「 Than 3 Big 」 and 「 Than 3 Small 」 The two part , This process is called partition（ Divide ）.

We still use 「 Baffle method 」 Thought , You don't have to actually have two arrays to store these two parts , It's using two baffles , I've divided the intervals .

We use it 「 Two pointers 」（ It's the baffle ） Divide the array into 「 Three intervals 」, that

• The range on the left is used to put less than pivot The elements of ;
• The range on the right is used to put greater than pivot The elements of ;
• In the middle is the unsorted interval .

So when initializing , We need to make sure 「 Unordered range 」 Be able to contain except 3 All the elements beyond , therefore

• Unordered range = [i, j]

So the left and right sections become ：

• [0, i)： Compare 3 Small number ;
• (j, array.length -2]： Compare 3 Large number

Be careful ️ i, j It's not included in the left and right ranges .

So our goal is check Every number in an unsorted interval , And put it in the right range , To narrow the unsorted range , Until there are no unordered elements .

From left to right check：

Step1.

5 > 3, therefore 5 Put it in the right range , therefore 5 and j Point to the 0 In exchange ：

such 5 Just line up , The pointer j --, So our unsorted interval is one less number ;

Step2.

0 < 3, So it should be on the left , direct i++;

Step3.

2 < 3, Empathy ,i++;

Step4.

1 < 3, Empathy ,i++;

So when the two hands are out of place , We end the cycle .

But it's one step short ,3 Not in the right place . So insert it between two intervals , That is, with the pointer i In exchange .

Sister Qi declared that ： We are not encouraged to put pivot On the far left .

Basically all the books are on the right , Since the left and right sides are the same , We will follow the default of everyone 、 Come to a consensus , There's no need to “ new in order to be different ”.

For example, the four stars in go , But what pays attention to chess is to set your own star position first , Instead of reaching out to the opponent's side .

Then when we put pivot After changing back to the right position , Whole partition It's over .

And then it's recursive , Just sort the left and right sides .

Finally, there are two questions I would like to discuss with you ：

1. Back to the beginning choice pivot The problem of , Take the last one every time , How about this ？

answer ： Not good .

Because we want to split the array More even , Uniform time complexity is lower ; But if it's an ordered array , So the last one is always the most uneven one .

So it should be Random take pivot, In this way, we can avoid the situation that the array itself always gets the maximum value .

2. pivot Where to put it

After random selection , We still have to take this pivot To the far right of the entire array , So our unsorted interval is Successive , Otherwise, every time I walk to pivot There's also the thought of skipping it , I'm so tired .

class Solution {
  public void quickSort(int[] array) {
    if (array == null || array.length <= 1) {
      return;
    }
    quickSort(array, 0, array.length - 1);
  }
  private void quickSort(int[] array, int left, int right) {
    // base case
    if (left >= right) {
      return;
    }

    // partition
    Random random = new Random(); // java.util  The random number generator in 
    int pivotIndex = left + random.nextInt(right - left + 1);
    swap(array, pivotIndex, right);

    int i = left;
    int j = right-1;
    while (i <= j) {
      if (array[i] <= array[right]) {
        i++;
      } else {
        swap(array, i, j);
        j--;
      }
    }
    swap(array, i, right);

    //「 branch 」
    quickSort(array, left, i-1);
    quickSort(array, i+1, right);
  }
  private void swap(int[] array, int x, int y) {
    int tmp = array[x];
    array[x] = array[y];
    array[y] = tmp;
  }
}

The space-time complexity here has a lot to do with whether the points are uniform or not , So let's look at the situation ：

1. Divide equally

Time complexity

If you can divide it almost evenly every time , that

• This is the main time of each cycle while In circulation , That is to say O(right - left);
• If it's even, it's logn layer ;
• So the total time is O(nlogn).

Spatial complexity

• The height of the recursive tree is logn,
• The space complexity of each floor is O(1),
• So the total spatial complexity is O(logn).

2. Most uneven

If you can get the maximum every time / minimum value , So the recursive tree looks like this ：

Time complexity

As shown in the figure above ：O(n^2)

Spatial complexity

The height of this recursive tree becomes O(n).

3. summary

Actually , Most of the time it will be close to uniform The situation of , So the uniform case is a average case.

Why does it seem like the best is actually an average situation ？

Because even if you don't get to the middle point , For example, it is divided into 10% and 90% The numbers on both sides , In fact, the time of each floor is still O(n), It's just The number of layers has changed to 9 At the bottom of the log, The total time is still O(nlogn).

So the average time complexity of the fast queue is O(nlogn).

stability

Then you should be able to see it , stay swap When , Has broken the relative order between the elements , So fast platoon is not stable .

We also answer the question at the beginning , Namely

• Why for primitive type Use fast platoon ,

  • Because it's the fastest ;

• Why for object Use merge ,

  • Because it's stable and fast .

That's all the content of the quick queue , It's also a very common test ！ In the next article, I'll talk about a few topics extended from quick scheduling , Guess what it is ？

If you like this article , Remember to leave me a like message ～ Your support and recognition , It's the biggest driving force of my creation , See you in the next article ！

This is Qi , New York program , Lifelong learners , Every night 9 spot , Let's meet you in the cloud study room ！

See my... For more dry articles Github: https://github.com/xiaoqi6666/NYCSDE