Python machine learning algorithm: linear regression

flutter + Applet + Back end ,3 Individuals can open your APP The way | Registration will be sent to Dajiang Yuntai 、 Huawei watch ！>>>

author |Vagif Aliyev compile |VK source |Towards Data Science

Linear regression is probably one of the most common algorithms , Linear regression is what machine learning practitioners must know . This is usually the first time a beginner comes into contact with machine learning algorithms , Understanding how it works is essential to better understand it .

therefore , In short , Let's break down the real problem ： What is linear regression ？

Linear regression defines

Linear regression is a supervised learning algorithm , The purpose of this paper is to use a linear method to model the relationship between dependent variables and independent variables . let me put it another way , Its goal is to fit a linear trend line that best captures data relationships , also , From this line , It can predict what the target value might be .

Great , I know the definition of it , But how does it work ？ Good question ！ To answer this question , Let's take a closer look at how linear regression works ：

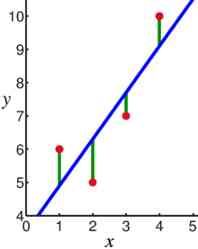
1. Fitting data （ As shown in the figure above ）.

2. Calculate the distance between points （ The red dots on the picture are dots , The green line is the distance ）, And then square it , Then sum it （ These values are squared , To ensure that negative values do not produce incorrect values and hinder the calculation of ）. This is the error of the algorithm , Or better known as residual

3. Store the residuals of iterations

4. Based on an optimization algorithm , Make the line a little bit “ Move ”, So that the line can better fit the data .

5. Repeat step 2-5, Until the desired result is achieved , Or the residual error is reduced to zero .

This method of fitting straight lines is called the least square method .

The mathematics behind linear regression

If you already understand, please feel free to skip this section

The linear regression algorithm is as follows ：

It can be simplified as ：

The following algorithm will basically complete the following operations ：

1. Accept one Y vector （ Your data tags ,（ housing price , Stock price , wait …）

This is your target vector , It will be used later to evaluate your data （ I'll talk about it in detail later ）.

2. matrix X（ The characteristics of the data ）：

This is the characteristic of the data , Age 、 Gender 、 Gender 、 Height, etc . This is the data that the algorithm actually uses to predict . Notice how there is a feature 0. This is called the intercept term , And always equal to 1.

3. Take a weight vector , And transpose it ：

This is the magic of the algorithm . All the eigenvectors are multiplied by these weights . This is called dot product . actually , You will try to find the best combination of these values for a given dataset . This is called optimization .

4. Get the output vector ：

This is the prediction vector from the data . then , You can use the cost function to evaluate the performance of the model .

This is basically the whole algorithm expressed mathematically . Now you should have a solid understanding of the function of linear regression . But the problem is , What is an optimization algorithm ？ How do we choose the best weight ？ How we evaluate performance ？

cost function

The cost function is essentially a formula , Used to measure the loss of a model or “ cost ”. If you've ever been to any Kaggle match , You may have come across some . Some common methods include ：

• Mean square error

• Root mean square error

• Mean absolute error

These functions are essential for model training and development , Because they answer “ How well does my model predict new instances ” This basic question ？”. Remember that , Because it's about our next topic .

optimization algorithm

Optimization is usually defined as improving something , The process of bringing it to its full potential . This also applies to machine learning . stay ML In the world of , Optimization is essentially trying to find the best combination of parameters for a data set . It's basically machine learning “ Study ” part .

I'll talk about the two most common algorithms ： Gradient descent method and standard equation .

gradient descent

Gradient descent is an optimization algorithm , To find the minimum value of a function . It does this by iteratively taking steps in the negative direction of the gradient . In our case , Gradient descent constantly updates the weight by moving the slope of the function tangent .

A concrete example of gradient descent

To better illustrate the gradient descent , Let's take a simple example . Imagine a man on the top of a mountain , He / She wants to climb to the bottom of the mountain . What they might do is look around , See which way to take a step , To get down faster . then , They may take a step in this direction , Now they're closer to the goal . However , They have to be careful when they come down , Because they can get stuck at some point , So we have to make sure that we choose our step size accordingly .

---

Again , The goal of gradient descent is to minimize the function . In our case , This is to minimize the cost of our model . It does this by finding the tangent of the function and moving in that direction . Algorithm “ step ” The size of is defined by the known learning rate . This basically controls the distance we move down . Use this parameter , We have to pay attention to two situations ：

1. Too fast to learn , The algorithm may not converge （ Minimum value reached ） And bounce around the minimum , But it will never reach that value

2. The learning rate is too low , The algorithm will take too long to reach the minimum , It may be “ card ” On a secondary advantage .

We have another parameter , It controls how many times the algorithm iterates the dataset .

Visually , The algorithm will do the following ：

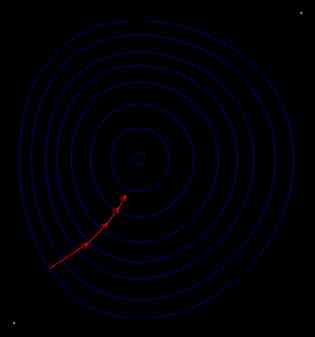
Because this algorithm is very important for machine learning , Let's take a look at what it does ：

1. Random initialization weights . This is called random initialization

2. then , The model uses these random weights to predict

3. The prediction of the model is evaluated by the cost function

4. Then the model runs gradient down , Find the tangent of the function , And then take a step on the slope of the tangent

5. The process will repeat N Sub iteration , Or if a condition is met .

Advantages and disadvantages of gradient descent method

advantage ：

1. It is possible to reduce the cost function to a global minimum （ Very close to or =0）

2. One of the most effective optimization algorithms

shortcoming ：

1. It can be slow on large datasets , Because it uses the entire dataset to calculate the gradient of the function tangent

2. It's easy to fall into a secondary advantage （ Or local minima ）

3. The user must manually select the learning rate and the number of iterations , It can be time-consuming

Now that we've introduced gradient descent , Now let's introduce the standard equation .

Standard equation （Normal Equation）

If we go back to our example , Instead of taking the next step , We will be able to get to the bottom immediately . That's what the standard equation looks like . It uses linear algebra to generate weights , It can produce as good a result as a gradient descent in a very short time .

The advantages and disadvantages of the standard equation

advantage

1. There is no need to choose the learning rate or the number of iterations

2. Very fast

shortcoming

1. It doesn't scale well to large datasets

2. Tends to produce good weight , But not the best weight

Feature scaling

This is an important preprocessing step for many machine learning algorithms , Especially those that use distance measurement and calculation （ Such as linear regression and gradient descent ） The algorithm of . It's essentially scaling our features , Make them in similar ranges . Think of it as a house , A scale model of a house . The shape of the two is the same （ They are all houses ）, But the size is different （5 rice ！=500 rice ）. We do this for the following reasons ：

1. It speeds up the algorithm

2. Some algorithms are scale sensitive . In other words , If features have different scales , It is possible to give a higher weight to a feature with a higher order of magnitude . This will affect the performance of machine learning algorithms , obviously , We don't want our algorithm to be biased towards a feature .

To demonstrate this , Suppose we have three characteristics , Named as A、B and C：

• Before zooming AB distance =>

• Before zooming BC distance =>

• After zooming AB distance =>

• After zooming BC Distance of =>

We can see clearly that , These features are more comparable and unbiased than before scaling .

Write linear regression from scratch

ok , Now the moment you've been waiting for ; Realization ！

Be careful ： All the code can be taken from this Github repo download . however , I suggest you follow the tutorial before you do this , Because then you'll have a better understanding of what code you're actually writing ：

https://github.com/Vagif12/ML-Algorithms-From-Scratch/blob/main/Linear%20Regression%20from%20Scratch.ipynb

First , Let's do some basic import ：

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_boston

Yes , That's all you need to import ！ We use numpy As a mathematical realization ,matplotlib Used to draw graphics , as well as scikitlearn Of boston Data sets .

#  Load and split data 
data = load_boston()
X,y = data['data'],data['target']

Next , Let's create a custom train_test_split function , Split our data into a training and test set ：

#  Split training and test sets 
def train_test_divide(X,y,test_size=0.3,random_state=42):
    np.random.seed(random_state)
    train_size = 1 - test_size
    arr_rand = np.random.rand(X.shape[0])
    split = arr_rand < np.percentile(arr_rand,(100*train_size))
    
    X_train = X[split]
    y_train = y[split]
    X_test =  X[~split]
    y_test = y[~split]
    
    return X_train, X_test, y_train, y_test
X_train,X_test,y_train,y_test = train_test_divide(X,y,test_size=0.3,random_state=42)

Basically , We're doing

1. Get the test set size .

2. Set a random seed , To ensure our results and repeatability .

3. According to the test set size, get the training set size

4. Random sampling from our features

5. The randomly selected instances are divided into training set and test set

Our cost function

We will achieve MSE Or mean square error , A common cost function for regression tasks ：

def mse(preds,y):
        m = len(y)
        return 1/(m) * np.sum(np.square((y - preds)))

• M It refers to the number of training instances

• yi It refers to an instance of our tag vector

• preds It's our prediction

In order to write clean 、 Repeatable and efficient code , And follow software development practices , We're going to create a class of linear regression ：

class LinReg:
    def __init__(self,X,y):
        self.X = X
        self.y = y
        self.m = len(y)
        self.bgd = False

• bgd It's a parameter , It defines whether we should use batch gradient descent .

Now we're going to create a method to add a intercept entry ：

def add_intercept_term(self,X):
        X = np.insert(X,1,np.ones(X.shape[0:1]),axis=1).copy()
        return X

This is basically inserting a column at the beginning of our feature . It's just for matrix multiplication .

If we don't add that , So we're going to force the hyperplane through the origin , And it tilts so much , So the data can't be fitted correctly

Zoom our features ：

def feature_scale(self,X):
        X = (X - X.mean()) / (X.std())
        return X

Next , We're going to initialize the weights randomly ：

def initialise_thetas(self):
        np.random.seed(42)
        self.thetas = np.random.rand(self.X.shape[1])

Now? , We will use the following formula to write standard equations from scratch ：

def normal_equation(self):
        A = np.linalg.inv(np.dot(self.X.T,self.X))
        B = np.dot(self.X.T,self.y)
        thetas = np.dot(A,B)
        return thetas

Basically , We divide the algorithm into three parts ：

1. We got X After transposition and X The inverse of the dot product of

2. We get the dot product of the weight and the label

3. We get the dot product of two calculated values

This is the standard equation ！ Not bad ！ Now? , We will use the following formula to achieve batch gradient descent ：

def batch_gradient_descent(self,alpha,n_iterations):
        self.cost_history = [0] * (n_iterations)
        self.n_iterations = n_iterations
        
        for i in range(n_iterations):
            h = np.dot(self.X,self.thetas.T)
            gradient = alpha * (1/self.m) * ((h - self.y)).dot(self.X)
            
            self.thetas = self.thetas - gradient
            self.cost_history[i] = mse(np.dot(self.X,self.thetas.T),self.y)
            
        return self.thetas

ad locum , We do the following ：

1. We set up alpha, Or the learning rate , And the number of iterations

2. We create a list to store our cost function history , In order to draw in the line chart later

3. loop n_iterations Time ,

4. We get predictions , And calculate the gradient （ The slope of the tangent to the function ）.

5. We update the weights to move in the negative direction of the gradient

6. We use our custom MSE Function records values

7. repeat , After completion , Return results

Let's define a fitting function for our data ：

def fit(self,bgd=False,alpha=0.158,n_iterations=4000):
        self.X = self.add_intercept_term(self.X)
        self.X = self.feature_scale(self.X)
        if bgd == False:
            
            self.thetas = self.normal_equation()
        else:
            self.bgd = True
            self.initialise_thetas()
            self.thetas = self.batch_gradient_descent(alpha,n_iterations)

ad locum , We just need to check whether users need gradient descent , And follow our steps accordingly .

Let's build a function to plot the cost function ：

def plot_cost_function(self):
        
        if self.bgd == True:
            plt.plot(range((self.n_iterations)),self.cost_history)
            plt.xlabel('No. of iterations')
            plt.ylabel('Cost Function')
            plt.title('Gradient Descent Cost Function Line Plot')
            plt.show()
        else:
            print('Batch Gradient Descent was not used!')

The last way to predict unmarked instances ：

def predict(self,X_test):
        self.X_test = X_test.copy()
        self.X_test = self.add_intercept_term(self.X_test)
        self.X_test = self.feature_scale(self.X_test)
        predictions = np.dot(self.X_test,self.thetas.T)
        return predictions

Now? , Let's see which optimization produces better results . First , Let's try gradient descent ：

lin_reg_bgd = LinReg(X_train,y_train)
lin_reg_bgd.fit(bgd=True)

mse(y_test,lin_reg_bgd.predict(X_test))

OUT:
28.824024414708344

Let's draw our function , See how the cost function is reduced ：

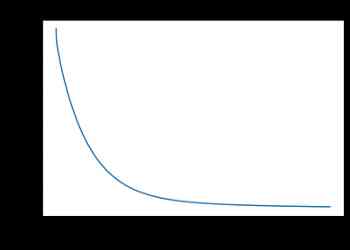
So we can see , At about 1000 Times of iteration , It's starting to converge .

Now the standard equation is ：

lin_reg_normal = LinReg(X_train,y_train)
lin_reg_normal.fit()

mse(y_test,lin_reg_normal.predict(X_test))

OUT:
22.151417764247284

So we can see , The performance of the standard equation is slightly better than that of the gradient descent method . This may be because the data set is very small , And we didn't choose the best parameter for the learning rate .

future

1. Greatly improve the learning rate . What's going to happen ？

2. Do not apply feature scaling . Is there a difference ？

3. Try to study , See if you can implement a better optimization algorithm . Evaluate your model in the test set

---

It's really interesting to write this article , Although it's a little long , But I hope you learned something today .

Link to the original text ：https://towardsdatascience.com/machine-learning-algorithms-from-start-to-finish-in-python-linear-regression-aa8c1d6b1169

Welcome to join us AI Blog station ： http://panchuang.net/

sklearn Machine learning Chinese official documents ： http://sklearn123.com/

Welcome to pay attention to pan Chuang blog resource summary station ： http://docs.panchuang.net/