当前位置:网站首页>MATLAB小技巧(28)模糊综合评价
MATLAB小技巧(28)模糊综合评价
2022-07-05 08:23:00 【mozun2020】
MATLAB小技巧(28)模糊综合评价
前言
MATLAB进行图像处理相关的学习是非常友好的,可以从零开始,对基础的图像处理都已经有了封装好的许多可直接调用的函数,这个系列文章的话主要就是介绍一些大家在MATLAB中常用一些概念函数进行例程演示!
模糊综合评价法是一种基于模糊数学的综合评价方法。该综合评价法根据模糊数学的隶属度理论把定性评价转化为定量评价,即用模糊数学对受到多种因素制约的事物或对象做出一个总体的评价。它具有结果清晰,系统性强的特点,能较好地解决模糊的、难以量化的问题,适合各种非确定性问题的解决。
模糊综合评价法的最显著特点是:
相互比较
以最优的评价因素值为基准,其评价值为1;其余欠优的评价因素依据欠优的程度得到相应的评价值。函数关系
可以依据各类评价因素的特征,确定评价值与评价因素值之间的函数关系(即:隶属度函数)。确定这种函数关系(隶属度函数)有很多种方法,例如,F统计方法,各种类型的F分布等。当然,也可以请有经验的评标专家进行评价,直接给出评价值。
在招标文件的编制中,应依据项目的具体情况,有重点地选择评价因素,科学地确定评价值与评价因素值之间的函数关系以及合理地确定评价因素的权重。模糊综合评价的一般步骤:
模糊综合评价指标的构建
模糊综合评价指标体系是进行综合评价的基础,评价指标的选取是否适宜,将直接影响综合评价的准确性。进行评价指标的构建应广泛涉猎与该评价指标系统行业资料或者相关的法律法规。采用构建好权重向量
通过专家经验法或者AHP层次分析法构建好权重向量。构建隶属矩阵
建立适合的隶属函数从而构建好隶属矩阵。隶属矩阵和权重的合成
采用适合的合成因子对其进行合成,并对结果向量进行解释。
仿真示例MATLAB版本为MATLAB2015b。
一. MATLAB仿真
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%功能:本程序为模糊综合评判的程序,人为给定权重
%环境:Win7,Matlab2015b
%Modi: C.S
%时间:2022-06-27
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%% I. 清空环境变量
clear all
clc
tic
%--------------------------------------------------------------------------
%程序运行,直接输入命令mohu即可
%本程序可以进行扩展
%对于进行二级模糊综合评判,可编制mohufun.m函数来实现
%如[yy1,qdh,qdh1]=mohufun(R,L,M,w,XX,yy]来实现运行两次这个函数,并编制相应的m文件,其中放至两个这样的函数即可实现
%模糊评判的结果说明:
%1:对于所有等级的隶属度之和为1。
%2:输出结果随某个变量的增大而qdh1的结果呈现出单调递增或递减
%3:最后的等级出[0.2 0 0 0.8]这种情况是正常的,和可拓评判中的对于等级的距离的概念是不一样的。
%只表现有变量是属于0.2这个等级的。
%--------------------------------------------------------------------------
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%此部分由计算时,人为给定部分,即相关求解条件
%要求计算前输入部分
R=4; %影响因素的个数
L=4; %评判的等级个数
M=29; %待评价洞段的个数
w=[0.1 0.7 0.1 0.1];%各指标的权重
%可拓评判的经典域,每天列构成一组,共有L组,由左到右依此为1,2,3,4
%评判结果为1,则表示属于最左边的经典域,为4则属于最右边的经典域
%XX为隶属函数的范围,具体可参见论文基于粗集的模糊综合评判,一个有四个隶属函数
%前两个数,确定是一个下降段的隶属函数,分成三段
%以后依此4上数为一组,确定一个梯形的隶属函数,分成五段
%最后两个是单独一组,为一个上升段的隶属函数分成三段
%下面的每行有12个数,其分成4个等级,分办界点数个2 4 4 2 之和为12
%也就是构成四个等级范围
%XX也是计算的核心数据
xx=[70 90 70 90 110 130 110 130 170 190 170 190
45 35 45 35 30 20 30 20 17 10 17 10
1.5 2.5 1.5 2.5 3 4 3 4 4.5 5.5 4.5 5.5
0.25 0.35 0.25 0.35 0.45 0.55 0.45 0.55 0.65 0.75 0.65 0.75];
%pp1为个指标为越大,等级越高,还是越大,等级越小的指标
%0为指标值越大,等级越大
%1为指标值越大,等级越小
%这一点要严格执行,XX(i,:),从小到大为0,XX(i,:)从大到小为1,
%若将以上的XX第行的顺序颠倒,则为pp1=[1 0 1 1 ]
pp1=[0 1 0 0];
%各待评价洞段参数
yy=[200 8 6 0.8
200 9.5 6 0.8
200 11 6 0.8
200 12.5 6 0.8
200 14 6 0.8
200 15.5 6 0.8
200 17 6 0.8
200 18.5 6 0.8
200 20 6 0.8
200 21.5 6 0.8
200 23 6 0.8
200 24.5 6 0.8
200 26 6 0.8
200 27.5 6 0.8
200 29 6 0.8
200 30.5 6 0.8
200 32 6 0.8
200 33.5 6 0.8
200 35 6 0.8
200 36.5 6 0.8
200 38 6 0.8
200 39.5 6 0.8
200 41 6 0.8
200 42.5 6 0.8
200 44 6 0.8
200 45.5 6 0.8
200 47 6 0.8
200 48.5 6 0.8
200 50 6 0.8
];
%下升段和下降段的隶属函数形式
%注意隶属函数的形式和论文中的隶属函数形式也要一样,否则要更改程序中的基些部分
%这里的a指区间的中间点,b指区间的宽度
f1=inline('0.5-0.5*sin((x-a)*pi/b)','a','b','x');
f2=inline('0.5+0.5*sin((x-a)*pi/b)','a','b','x');
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%求每个指标对于第一个等级的隶属度
for i=1:M,
for k=1:R,
j=1;
if pp1(k)==0 %先是求越大,等级越高的指标
if yy(i,k)<xx(k,j)
yy1(i,k,j)=1;
elseif yy(i,k)<=xx(k,j+1)
yy1(i,k,j)=f1(0.5*(xx(k,j)+xx(k,j+1)),abs(xx(k,j)-xx(k,j+1)),yy(i,k)) ;
else yy1(i,k,j)=0;
end
%再是求值越小,等级越高的指标
%下在和一个相比大于和小于要互换,函数f1和f2也要互换
elseif yy(i,k)>xx(k,j)
yy1(i,k,j)=1;
elseif yy(i,k)>=xx(k,j+1)
yy1(i,k,j)=f2(0.5*(xx(k,j)+xx(k,j+1)),abs(xx(k,j)-xx(k,j+1)),yy(i,k));
else yy1(i,k,j)=0;
end
end
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%求每个指标对于最后一个等级的隶属度
for i=1:M,
for k=1:R,
j=L;
if pp1(k)==0 %先是求越大,等级越高的指标
if yy(i,k)<xx(k,j*4-5)
yy1(i,k,j)=0;
elseif yy(i,k)<=xx(k,j*4-4)
yy1(i,k,j)=f2(0.5*(xx(k,j*4-5)+xx(k,j*4-4)),abs(xx(k,j*4-5)-xx(k,j*4-4)),yy(i,k));
else yy1(i,k,j)=1;
end
%再是求值越小,等级越高的指标
%下在和一个相比大于和小于要互换,函数f1和f2也要互换
elseif yy(i,k)>xx(k,j*4-5)
yy1(i,k,j)=0;
elseif yy(i,k)>=xx(k,j*4-4)
yy1(i,k,j)=f1(0.5*(xx(k,j*4-5)+xx(k,j*4-4)),abs(xx(k,j*4-5)-xx(k,j*4-4)),yy(i,k)) ;
else yy1(i,k,j)=1;
end
end
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%求每个指标对于中间几个等级的隶属度
for i=1:M,
for k=1:R,
for j=2:L-1;
if pp1(k)==0 %先是求越大,等级越高的指标
if yy(i,k)<xx(k,j*4-5)
yy1(i,k,j)=0;
elseif yy(i,k)<=xx(k,j*4-4)
yy1(i,k,j)=f2(0.5*(xx(k,j*4-5)+xx(k,j*4-4)),abs(xx(k,j*4-5)-xx(k,j*4-4)),yy(i,k));
elseif yy(i,k)<=xx(k,j*4-3)
yy1(i,k,j)=1;
elseif yy(i,k)<=xx(k,j*4-2)
yy1(i,k,j)=f1(0.5*(xx(k,j*4-3)+xx(k,j*4-2)),abs(xx(k,j*4-3)-xx(k,j*4-2)),yy(i,k)) ;
else yy1(i,k,j)=0;
end
%再是求值越小,等级越高的指标
%下在和一个相比大于和小于要互换,函数f1和f2也要互换
elseif yy(i,k)>xx(k,j*4-5)
yy1(i,k,j)=0;
elseif yy(i,k)>=xx(k,j*4-4)
yy1(i,k,j)=f1(0.5*(xx(k,j*4-5)+xx(k,j*4-4)),abs(xx(k,j*4-5)-xx(k,j*4-4)),yy(i,k));
elseif yy(i,k)>=xx(k,j*4-3)
yy1(i,k,j)=1;
elseif yy(i,k)>=xx(k,j*4-2)
yy1(i,k,j)=f2(0.5*(xx(k,j*4-3)+xx(k,j*4-2)),abs(xx(k,j*4-3)-xx(k,j*4-2)),yy(i,k)) ;
else yy1(i,k,j)=0;
end
end
end
end
% %相乘计算,隶属度乘权重各洞段对每一等级的隶属度,取最大值
%dot函数为内积函数,为两向量各对应分量相等后再求和
for i=1:M,
for j=1:L,
qdh(i,j)=dot(yy1(i,:,j),w);
end
end
%隶属度乘等级值,确定级别
% %qdh为评价结果,取最大的,属于哪一个等级
% qdh1,等级值
for i=1:M,
for j=1:L,
[maxlevel(i),qdh1(i)]=max(qdh(i,:));
end
disp(['样本',num2str(i),'对应分类为:',num2str(qdh1(i))]);
end
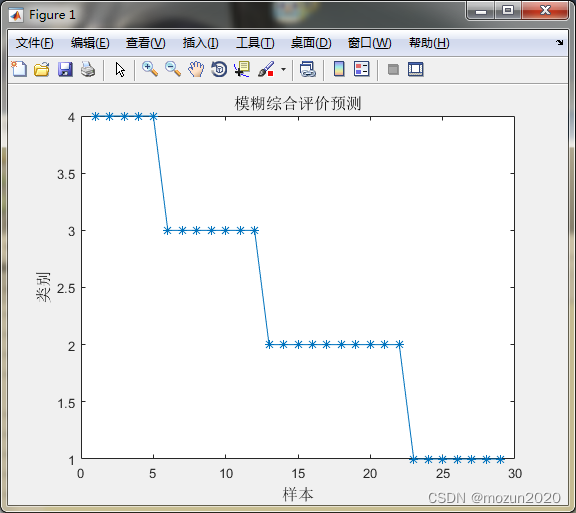
figure(1)
plot(qdh1(1:29),'-*');
title('模糊综合评价预测','fontsize',12)
xlabel('样本','fontsize',12)
ylabel('类别','fontsize',12)
toc
二. 仿真结果
样本1对应分类为:4
样本2对应分类为:4
样本3对应分类为:4
样本4对应分类为:4
样本5对应分类为:4
样本6对应分类为:3
样本7对应分类为:3
样本8对应分类为:3
样本9对应分类为:3
样本10对应分类为:3
样本11对应分类为:3
样本12对应分类为:3
样本13对应分类为:2
样本14对应分类为:2
样本15对应分类为:2
样本16对应分类为:2
样本17对应分类为:2
样本18对应分类为:2
样本19对应分类为:2
样本20对应分类为:2
样本21对应分类为:2
样本22对应分类为:2
样本23对应分类为:1
样本24对应分类为:1
样本25对应分类为:1
样本26对应分类为:1
样本27对应分类为:1
样本28对应分类为:1
样本29对应分类为:1
时间已过 0.075994 秒。
三. 小结
模糊综合评价法(fuzzy comprehensive evaluation method)是模糊数学中最基本的数学方法之一,该方法是以隶属度来描述模糊界限的。由于评价因素的复杂性、评价对象的层次性、评价标准中存在的模糊性以及评价影响因素的模糊性或不确定性、定性指标难以定量化等一系列问题,使得人们难以用绝对的“非此即彼”来准确的描述客观现实,经常存在着“亦此亦彼”的模糊现象,其描述也多用自然语言来表达,而自然语言最大的特点是它的模糊性,而这种模糊性很难用经典数学模型加以统一量度。因此,建立在模糊集合基础上的模糊综合评判方法,从多个指标对被评价事物隶属等级状况进行综合性评判,它把被评判事物的变化区间做出划分,一方面可以顾及对象的层次性,使得评价标准、影响因素的模糊性得以体现;另一方面在评价中又可以充分发挥人的经验,使评价结果更客观,符合实际情况。模糊综合评判可以做到定性和定量因素相结合,扩大信息量,使评价数度得以提高,评价结论可信。
传统的综合评价方法很多,应用也较为广泛,但是没有一种方法能够适合各种场所,解决所有问题,每一种方法都有其侧重点和主要应用领域。如果要解决新的领域内产生的新问题,模糊综合法显然更为合适。模糊评价法奠基于模糊数学。模糊数学诞生于1965年,他的创始人美国自动控制专家L.A.Zadeh。20世纪80年代后期,日本将模糊技术应用于机器人、过程控制、地铁机车、交通管理、故障诊断、医疗诊断、声音识别、图像处理、市场预测等众多领域。模糊理论及模糊法在日本的应用和巨大的市场前景,给西方企业界很大震动,在学术界也得到了普遍的认同。国内对于模糊数学及模糊综合评价法的研究起步相对较晚,但在近些年各个领域(如医学、建筑业、环境质量监督、水利等)的应用也已初显成效。每天学一个MATLAB小知识,大家一起来学习进步阿!
边栏推荐
- MySQL之MHA高可用集群
- 实例007:copy 将一个列表的数据复制到另一个列表中。
- VESC Benjamin test motor parameters
- Design a clock frequency division circuit that can be switched arbitrarily
- Stm32--- systick timer
- 实例003:完全平方数 一个整数,它加上100后是一个完全平方数,再加上168又是一个完全平方数,请问该数是多少?
- 实例002:“个税计算” 企业发放的奖金根据利润提成。利润(I)低于或等于10万元时,奖金可提10%;利润高于10万元,低于20万元时,低于10万元的部分按10%提成,高于10万元的部分,可提成7.
- My-basic application 1: introduction to my-basic parser
- On boost circuit
- Talk about the circuit use of TVs tube
猜你喜欢
Explain task scheduling based on Cortex-M3 in detail (Part 2)

Solutions to compilation warnings in Quartus II
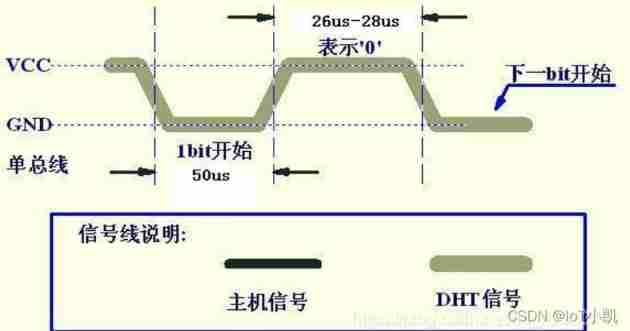
STM32 summary (HAL Library) - DHT11 temperature sensor (intelligent safety assisted driving system)
How to copy formatted notepad++ text?
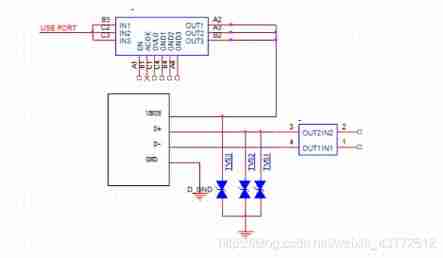
Talk about the circuit use of TVs tube
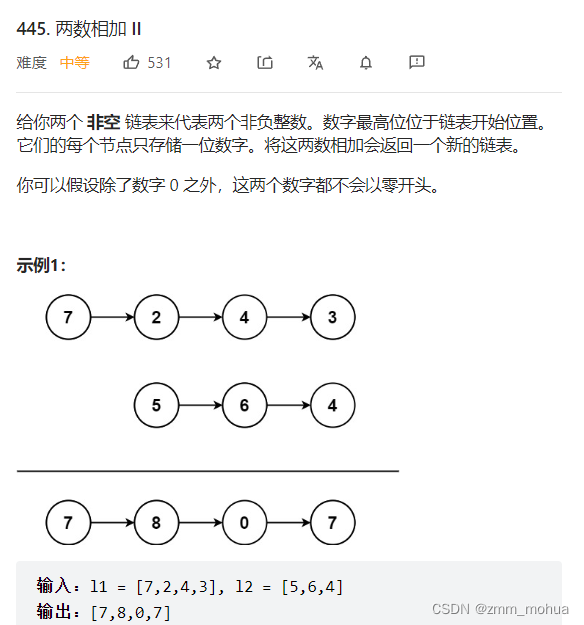
leetcode - 445. 两数相加 II
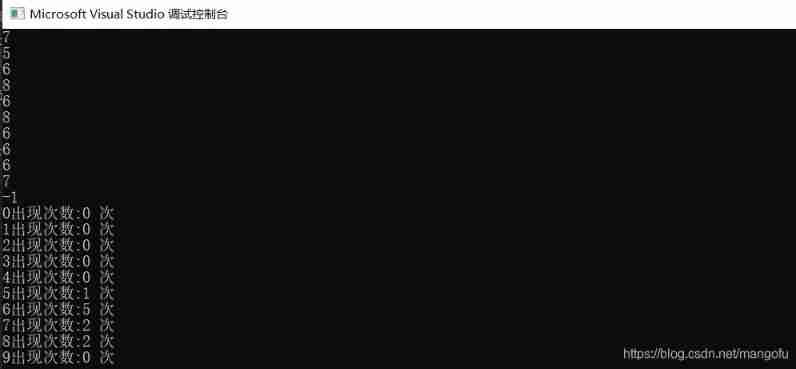
Count the number of inputs (C language)
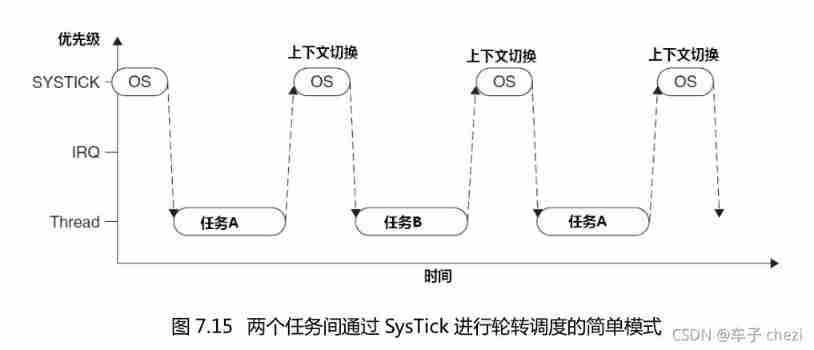
Explain task scheduling based on Cortex-M3 in detail (Part 1)
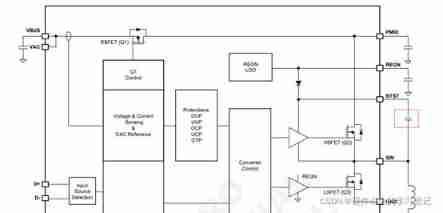
DCDC circuit - function of bootstrap capacitor
STM32 single chip microcomputer -- debug in keil5 cannot enter the main function
随机推荐
Several implementation schemes of anti reverse connection protection of positive and negative poles of power supply!
How to copy formatted notepad++ text?
My-basic application 1: introduction to my-basic parser
關於線性穩壓器的五個設計細節
Let's briefly talk about the chips commonly used in mobile phones - OVP chips
matlab timeserise
STM32 tutorial triple ADC interleaved sampling
Classic application of MOS transistor circuit design (1) -iic bidirectional level shift
STM32---IIC
Arduino uses nrf24l01+ communication
Negative pressure generation of buck-boost circuit
[paper reading] the latest transfer ability in deep learning: a survey in 2022
Example 002: the bonus paid by the "individual income tax calculation" enterprise is based on the profit commission. When the profit (I) is less than or equal to 100000 yuan, the bonus can be increase
Working principle and type selection of common mode inductor
Hardware 3 -- function of voltage follower
Zero length array in GNU C
Example 003: a complete square is an integer. It is a complete square after adding 100, and it is a complete square after adding 168. What is the number?
Summary of SIM card circuit knowledge
Summary -st2.0 Hall angle estimation
Measurement fitting based on Halcon learning [III] PM_ measure_ board. Hdev routine