当前位置:网站首页>啃下大骨头——排序(二)
啃下大骨头——排序(二)
2022-07-04 22:17:00 【让一切都燃烧】
2.3 交换排序
基本思想:所谓交换,就是根据序列中两个记录键值的比较结果来对换这两个记录在序列中的位置,交换排序的特点是:将键值较大的记录向序列的尾部移动,键值较小的记录向序列的前部移动。
2.3.1冒泡排序
找到最大的数往后排
冒泡排序的特性总结:
- 冒泡排序是一种非常容易理解的排序
- 时间复杂度:O(N^2)
- 空间复杂度:O(1)
- 稳定性:稳定
代码
void BubbleSort(int* a, int n)
{
assert(a);
for (int j = 0; j < n; ++j)
{
int exchange = 0;
for (int i = 1; i < n - j; ++i)
{
if (a[i - 1]>a[i])
{
Swap(&a[i - 1], &a[i]);
exchange = 1;
}
}
//没交换
if (exchange == 0)
{
break;
}
}
}
与插入排序相比:
冒泡:N-1 + n-2
插入:N 接近有序或者是局部有序等等情况下,插入能更好的使用
2.3.2 快速排序
快速排序是
Hoare于1962年提出的一种二叉树结构的交换排序方法
其基本思想为:
任取待排序元素序列中的某元素作为基准值,按照该排序码将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,然后最左右子序列重复该过程,直到所有元素都排列在相应位置上为止
单趟:
选出一个key,一般是最左边或者是最右边
要求排完之后要求:左边比key要小,右边比key要大
上述为快速排序递归实现的主框架,发现与二叉树前序遍历规则非常像,同学们在写递归框架时可想想二叉树前序遍历规则即可快速写出来,后序只需分析如何按照基准值来对区间中数据进行划分的方式即可。
将区间按照基准值划分为左右两半部分的常见方式有:
1. hoare版本
选定最左边为key,R先从后往前走找到比key小的数(此时L是不动的,等R找完L再开始),然后L再从前往后走找到比key大的数,此时两者交换,然后继续,直到R与L相遇,将该位置的值与key交换
因为不是同时走,所以R与L不会错过。
左边是key为什么不能左边先走?
结论: 要保证相遇位置的值比key要小或者就是key的位置
两种情况:
1.R先走,R停下来,L去遇到R 此时相遇位置就是R停下来的位置,而R停下的条件就是遇到比key小的值,所以此时满足相遇位置比key要小的结论
2.R先走,R没有找到比key要小的值,R去遇了L
1)L没走,R直接与L相遇key的位置(与key相等
2)R与L已经走过一轮了,相遇位置是L的上一轮停下来的位置,此时这个位置比key要小。因为上一轮L已经与R交换了,所以此时L就是比key要小的数比key要小
结论建议:左边是key,右边先走 右边是key,左边先走
// [begin, end]
//N*log^N
void QuickSort(int* a, int begin, int end)
{
// 区间不存在,或者只有一个值则不需要在处理
if (begin >= end)
{
return;
}
int left = begin, right = end;
int keyi = left;
while (left < right)
{
// 右边先走,找小
while (left < right && a[right] >= a[keyi])
{
--right;
}
// 左边再走,找大
while (left < right && a[left] <= a[keyi])
{
++left;
}
Swap(&a[left], &a[right]);
}
Swap(&a[keyi], &a[left]);
keyi = left;
//递归
// [begin, keyi-1] keyi [keyi+1, end]
//左区间有序 + 右区间有序 = 整体有序
QuickSort(a, begin, keyi - 1);
QuickSort(a, keyi + 1, end);
}
2.挖坑法(hoare改良)
先选定一个key把它拿出来形成一个坑位
// 挖坑法
int PartSort2(int* a, int begin, int end)
{
int key = a[begin];
int piti = begin;
while (begin < end)
{
// 右边找小,填到左边的坑里面去。这个位置形成新的坑
while (begin < end && a[end] >= key)
{
--end;
}
a[piti] = a[end];
piti = end;
// 左边找大,填到右边的坑里面去。这个位置形成新的坑
while (begin < end && a[begin] <= key)
{
++begin;
}
a[piti] = a[begin];
piti = begin;
}
a[piti] = key;
return piti;
}
void QuickSort(int* a, int begin, int end)
{
//区间不存在,或者只有一个值则不需要处理
if (begin >= end)
{
return;
}
int keyi = PartSort2(a, begin, end);
//[begin, keyi-1] keyi [keyi+1, end]
QuickSort(a, begin, keyi-1);
QuickSort(a, keyi + 1, end);
}
3.前后指针法
选定最左边为key
cur指针找小(比key小),找到之后与prev交换,若cur越界那么perv与key交换
什么会影响快排的效率?
有序或者接近有序,key的值(选到最大或最小)
N + N-1 + N-2 + …
O(N^2)
数据量过大会出现栈溢出
方法:
1.随机选key
2.三数选中 在第一个,中间,最后一个当中选,选不是最大也不是最小的
//选出不是最大也不是最小的值
int GetMidIndex(int* a, int begin, int end)
{
int mid = (begin + end) / 2;
if (a[begin] < a[mid])
{
if (a[mid] < a[end])
{
return mid;
}
else if (a[begin] < a[end])
{
return end;
}
else
{
return begin;
}
}
else // (a[begin] >= a[mid])
{
if (a[mid] > a[end])
{
return mid;
}
else if (a[begin] < a[end])
{
return begin;
}
else
{
return end;
}
}
}
// 前后指针法
int PartSort3(int* a, int begin, int end)
{
int prev = begin;
int cur = begin + 1;
int keyi = begin;
// 加入三数取中的优化
int midi = GetMidIndex(a, begin, end);
Swap(&a[keyi], &a[midi]);
//大于了,相当于越界才会结束
while (cur <= end)
{
// cur位置的值小于keyi位置值——找小
if (a[cur] < a[keyi] && ++prev != cur)
//交换
Swap(&a[prev], &a[cur]);
++cur;//不管怎样cur一定都在往后走
}
Swap(&a[prev], &a[keyi]);
keyi = prev;
return keyi;
}
void QuickSort(int* a, int begin, int end)
{
//区间不存在,或者只有一个值则不需要处理
if (begin >= end)
{
return;
}
int keyi = PartSort3(a, begin, end);
//[begin, keyi-1] keyi [keyi+1, end]
QuickSort(a, begin, keyi-1);
QuickSort(a, keyi + 1, end);
}
2.3.2 快速排序优化
- 三数取中法选key
- 递归到小的子区间时,可以考虑使用插入排序
总递归调用次数:2^h-1
减少递归次数
当递归划分小区间,区间比较小的时候就不再递归去划分排序这个小区间。可以考虑直接使用其他排序去对小区间进行排序(插入排序)
假设区间小于10时,就不再递归排序小区间。差不多能减少80%的递归次数
void QuickSort(int* a, int begin, int end)
{
if (begin >= end)
{
return;
}
// 区间小于10时,就不再递归排序小区间
if (end - begin > 10)
{
int keyi = PartSort3(a, begin, end);
// [begin, keyi-1] keyi [keyi+1, end]
QuickSort(a, begin, keyi - 1);
QuickSort(a, keyi + 1, end);
}
else
{
InsertSort(a + begin, end - begin + 1);
}
}
2.3.2 快速排序非递归
因为要使用栈
所以记得引用Stack.h Stack.c
// 要求掌握,递归改非递归
// 递归大问题,极端场景下面,如果深度太深,会出现栈溢出
// 1、直接改循环 -- 比如斐波那契数列、归并排序
// 2、用数据结构栈模拟递归过程
void QuickSortNonR(int* a, int begin, int end)
{
ST st;
StackInit(&st);
StackPush(&st, end);
StackPush(&st, begin);
while (!StackEmpty(&st))
{
int left = StackTop(&st);
StackPop(&st);
int right = StackTop(&st);
StackPop(&st);
int keyi = PartSort3(a, left, right);
// [left, keyi-1] keyi[keyi+1, right]
if (keyi + 1 < right)
{
StackPush(&st, right);
StackPush(&st, keyi + 1);
}
if (left < keyi - 1)
{
StackPush(&st, keyi - 1);
StackPush(&st, left);
}
}
StackDestroy(&st);
}
快速排序的特性总结:
- 快速排序整体的综合性能和使用场景都是比较好的,所以才敢叫快速排序
- 时间复杂度:O(N*logN)
- 空间复杂度:O(logN)
- 稳定性:不稳定
2.4 归并排序
基本思想:
归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide andConquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
归并排序核心步骤:
先划分成左右两个子区间,如果两个子区间都有序就进行归并
(两个指针同时走,进行比较,谁小谁先到新区间里)
若左右区间无序,从左右区间分别一直划分成单个数,进行递归
先走一边
拥有两个数的有序左右区间归并成一个四个数的有序区间,然后拥有四个数的有序左右区间归并成最后的八位数的有序区间
1 2 4 8(可以不一定是2的倍数)
归并排序的特性总结:
- 归并的缺点在于需要O(N)的空间复杂度,归并排序的思考更多的是解决在磁盘中的外排序问题。
- 时间复杂度:O(N*logN)
- 空间复杂度:O(N)
- 稳定性:稳定
递归版本:
void _MergeSort(int* a, int begin, int end, int* tmp)
{
if (begin >= end)
return;
int mid = (begin + end) / 2;
// [begin, mid] [mid+1, end] 分治递归,让子区间有序
_MergeSort(a, begin, mid, tmp);//左
_MergeSort(a, mid + 1, end, tmp);//右
//归并 [begin, mid] [mid+1, end]
int begin1 = begin, end1 = mid;//左
int begin2 = mid + 1, end2 = end;//右
int i = begin1;//起始位置
while (begin1 <= end1 && begin2 <= end2)
{
//谁小谁先过去
if (a[begin1] < a[begin2])
{
tmp[i++] = a[begin1++];
}
else
{
tmp[i++] = a[begin2++];
}
}
//按理说,以下两个while只能进去一个
while (begin1 <= end1)
{
tmp[i++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[i++] = a[begin2++];
}
// 把归并数据拷贝回原数组
memcpy(a + begin, tmp + begin, (end - begin + 1)*sizeof(int));
}
void MergeSort(int* a, int n)
{
//第三新区间
int* tmp = (int*)malloc(sizeof(int)*n);
if (tmp == NULL)
{
printf("malloc fail\n");
exit(-1);
}
_MergeSort(a, 0, n - 1, tmp);
//释放第三方区间
free(tmp);
}
非递归版本:
//void MergeSortNonR(int* a, int n)
//{
// int* tmp = (int*)malloc(sizeof(int)*n);
// if (tmp == NULL)
// {
// printf("malloc fail\n");
// exit(-1);
// }
//
// int gap = 1;
// while (gap < n)
// {
// printf("gap=%d->", gap);
// for (int i = 0; i < n; i += 2 * gap)
// {
// // [i,i+gap-1][i+gap, i+2*gap-1]
// int begin1 = i, end1 = i + gap - 1;
// int begin2 = i + gap, end2 = i + 2 * gap - 1;
//
// // 越界-修正边界
// if (end1 >= n)
// {
// end1 = n - 1;
// // [begin2, end2]修正为不存在区间
// begin2 = n;
// end2 = n - 1;
// }
// else if (begin2 >= n)
// {
// // [begin2, end2]修正为不存在区间
// begin2 = n;
// end2 = n - 1;
// }
// else if(end2 >= n)
// {
// end2 = n - 1;
// }
//
// printf("[%d,%d] [%d, %d]--", begin1, end1, begin2, end2);
//
// int j = begin1;
// while (begin1 <= end1 && begin2 <= end2)
// {
// if (a[begin1] < a[begin2])
// {
// tmp[j++] = a[begin1++];
// }
// else
// {
// tmp[j++] = a[begin2++];
// }
// }
//
// while (begin1 <= end1)
// {
// tmp[j++] = a[begin1++];
// }
//
// while (begin2 <= end2)
// {
// tmp[j++] = a[begin2++];
// }
// }
//
// printf("\n");
// memcpy(a, tmp, sizeof(int)*n);
//
// gap *= 2;//1 2 4
// }
//
// free(tmp);
//}
void MergeSortNonR(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int)*n);
if (tmp == NULL)
{
printf("malloc fail\n");
exit(-1);
}
int gap = 1;
while (gap < n)
{
for (int i = 0; i < n; i += 2 * gap)
{
// [i,i+gap-1][i+gap, i+2*gap-1]
int begin1 = i, end1 = i + gap - 1;
int begin2 = i + gap, end2 = i + 2 * gap - 1;
// end1越界或者begin2越界,则可以不归并了
if (end1 >= n || begin2 >= n)
{
break;
}
else if (end2 >= n)
{
end2 = n - 1;
}
int m = end2 - begin1 + 1;
int j = begin1;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
tmp[j++] = a[begin1++];
}
else
{
tmp[j++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[j++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[j++] = a[begin2++];
}
memcpy(a + i, tmp + i, sizeof(int)* m);
}
gap *= 2;
}
free(tmp);
}
除此之外,还有一些排序:
桶排序
基数排序
计数排序
了解就好,不需要掌握。
2.5 非比较排序
适用于整数(负数也可以)
思想:计数排序又称为鸽巢原理,是对哈希直接定址法的变形应用。 操作步骤:
- 统计相同元素出现次数
- 根据统计的结果将序列回收到原来的序列中
局限性:
1.如果是浮点数、字符串就不能使用高
2.如果数据范围很大,空间复杂度就会很,不适合
3.适合范围集中重复数据较多
计数排序的特性总结:
- 计数排序在数据范围集中时,效率很高,但是适用范围及场景有限。
- 时间复杂度:O(MAX(N,范围))
- 空间复杂度:O(范围)
4.稳定性:稳定
// 时间复杂度:O(max(range, N))
// 空间复杂度:O(range)
void CountSort(int* a, int n)
{
int min = a[0], max = a[0];
for (int i = 1; i < n; ++i)
{
if (a[i] < min)
min = a[i];
if (a[i] > max)
max = a[i];
}
// 统计次数的数组
int range = max - min + 1;
int* count = (int*)malloc(sizeof(int)*range);
if (count == NULL)
{
printf("malloc fail\n");
exit(-1);
}
memset(count, 0, sizeof(int)*range);
// 统计次数
for (int i = 0; i < n; ++i)
{
count[a[i] - min]++;
}
// 回写-排序
int j = 0;
for (int i = 0; i < range; ++i)
{
// 出现几次就会回写几个i+min
while (count[i]--)
{
a[j++] = i + min;
}
}
}
边栏推荐
- POM in idea XML dependency cannot be imported
- Easy to use app recommendation: scan QR code, scan barcode and view history
- i. Mx6ull driver development | 24 - platform based driver model lights LED
- 都说软件测试很简单有手就行,但为何仍有这么多劝退的?
- LOGO特訓營 第一節 鑒別Logo與Logo設計思路
- PostgreSQLSQL高级技巧透视表
- Tiktok actual combat ~ the number of comments is updated synchronously
- 国产数据库乱象
- NFT Insider #64:电商巨头eBay提交NFT相关商标申请,毕马威将在Web3和元宇宙中投入3000万美元
- 如何实现轻松管理1500万员工?
猜你喜欢

NFT insider 64: e-commerce giant eBay submitted an NFT related trademark application, and KPMG will invest $30million in Web3 and metauniverse
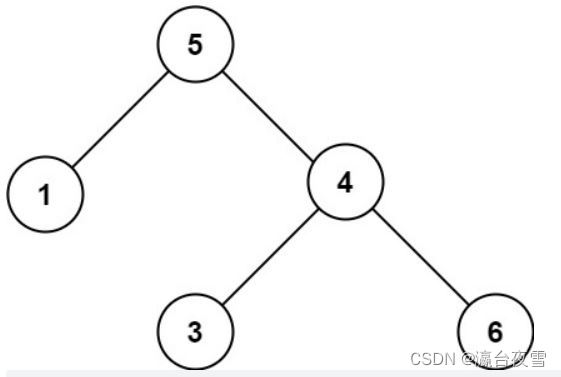
Li Kou 98: verify binary search tree

Naacl-22 | introduce the setting of migration learning on the prompt based text generation task
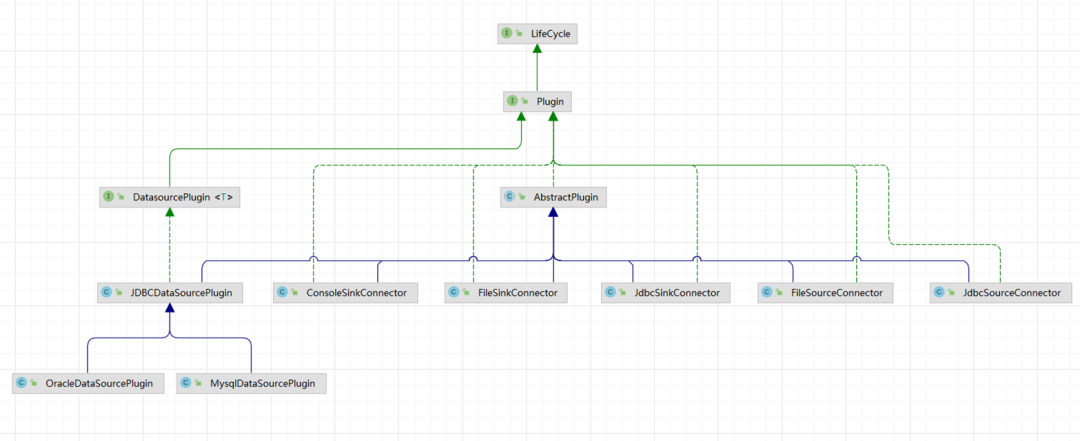
Visual task scheduling & drag and drop | scalph data integration based on Apache seatunnel
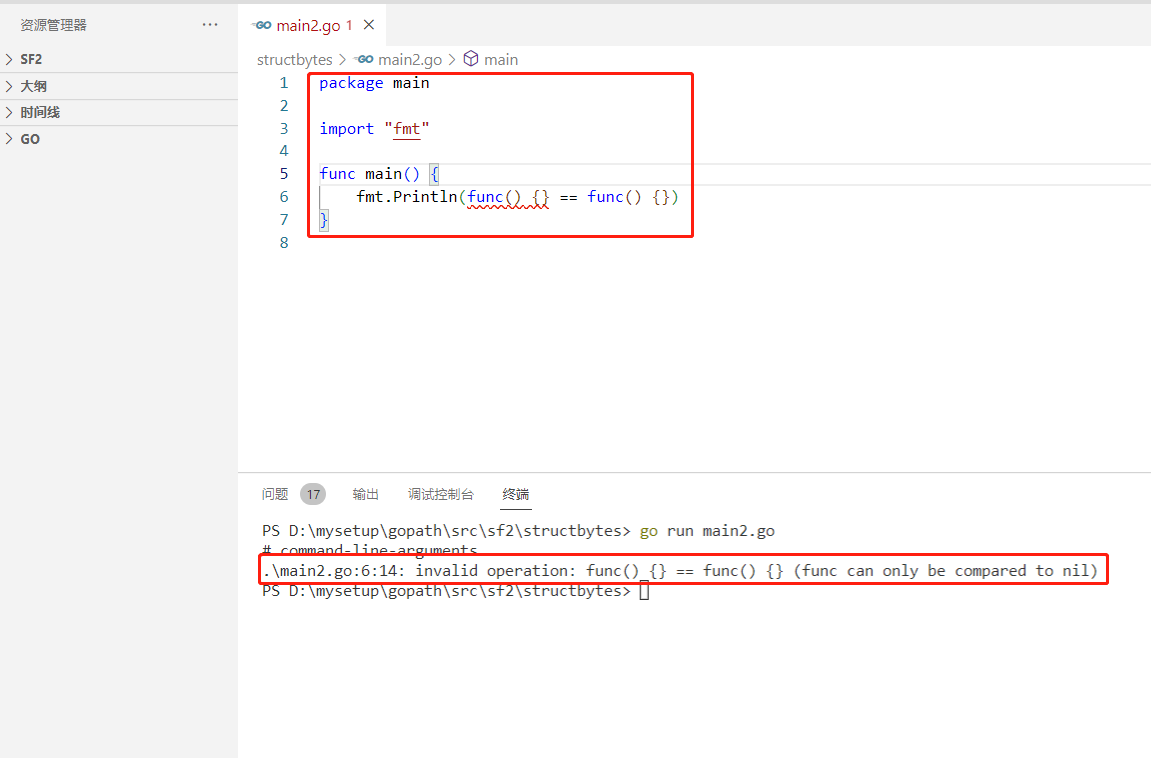
2022-07-04:以下go语言代码输出什么?A:true;B:false;C:编译错误。 package main import “fmt“ func main() { fmt.Pri

抖音实战~评论数量同步更新
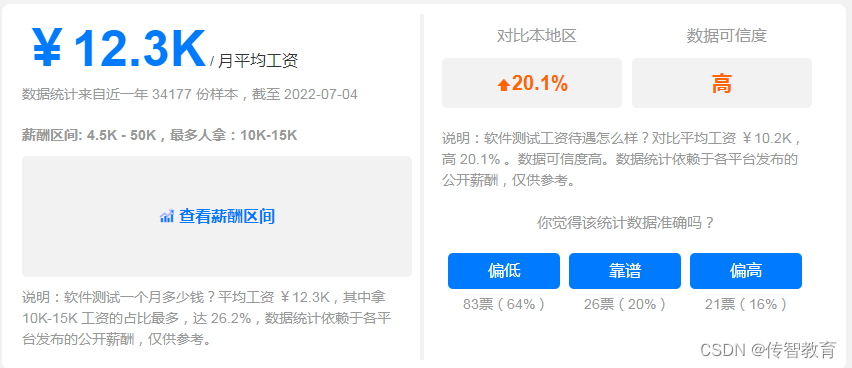
How to transfer to software testing, one of the high paying jobs in the Internet? (software testing learning roadmap attached)
With this PDF, we finally got offers from eight major manufacturers, including Alibaba, bytek and Baidu

It is said that software testing is very simple, but why are there so many dissuasions?

Deveco device tool 3.0 release brings five capability upgrades to make intelligent device development more efficient
随机推荐
Business is too busy. Is there really no reason to have time for automation?
Test will: bug classification and promotion solution
The use of complex numbers in number theory and geometry - Cao Zexian
Jvm-Sandbox-Repeater的部署
都说软件测试很简单有手就行,但为何仍有这么多劝退的?
Ascendex launched Walken (WLKN) - an excellent and leading "walk to earn" game
Tla+ introductory tutorial (1): introduction to formal methods
leetcode 72. Edit distance edit distance (medium)
Introducing QA into the software development lifecycle is the best practice that engineers should follow
In Linux, I call odspcmd to query the database information. How to output silently is to only output values. Don't do this
Flask 上下文详解
Google Earth Engine(GEE)——以MODIS/006/MCD19A2为例批量下载逐天AOD数据逐天的均值、最大值、最小值、标准差、方差统计分析和CSV下载(北京市各区为例)
LOGO特训营 第二节 文字与图形的搭配关系
Locust性能测试 —— 环境搭建及使用
More than 30 institutions jointly launched the digital collection industry initiative. How will it move forward in the future?
传智教育|如何转行互联网高薪岗位之一的软件测试?(附软件测试学习路线图)
Use blocconsumer to build responsive components and monitor status at the same time
Short video system source code, click the blank space of the screen, the keyboard does not automatically stow
【烹饪记录】--- 青椒炒千张
Domestic database chaos