当前位置:网站首页>[set theory] set identities (idempotent law | exchange law | combination law | distribution rate | De Morgan law | absorption rate | zero law | identity | exclusion law | contradiction law | complemen
[set theory] set identities (idempotent law | exchange law | combination law | distribution rate | De Morgan law | absorption rate | zero law | identity | exclusion law | contradiction law | complemen
2022-07-03 04:12:00 【Programmer community】
One 、 Set identity
1. Idempotent law :
A
∪
A
=
A
A \cup A = A
A∪A=A ,
A
∩
A
=
A
A \cap A = A
A∩A=A
2. Commutative law :
A
∪
B
=
B
∪
A
A \cup B = B \cup A
A∪B=B∪A ,
A
∩
B
=
B
∩
A
A \cap B = B \cap A
A∩B=B∩A
3. Associative law :
(
A
∪
B
)
∪
C
=
A
∪
(
B
∪
C
)
(A \cup B) \cup C = A \cup ( B \cup C )
(A∪B)∪C=A∪(B∪C) ,
(
A
∩
B
)
∩
C
=
A
∩
(
B
∩
C
)
(A \cap B) \cap C = A \cap ( B \cap C )
(A∩B)∩C=A∩(B∩C)
4. Distribution rate :
A
∪
(
B
∩
C
)
=
(
A
∪
B
)
∩
(
A
∪
C
)
A \cup ( B \cap C ) = ( A \cup B ) \cap ( A \cup C )
A∪(B∩C)=(A∪B)∩(A∪C) ,
A
∩
(
B
∪
C
)
=
(
A
∩
B
)
∪
(
A
∩
C
)
A \cap ( B \cup C ) = ( A \cap B ) \cup ( A \cap C )
A∩(B∪C)=(A∩B)∪(A∩C)
5. De Morgan law :
① absolute form :
∼
(
A
∪
B
)
=
∼
A
∩
∼
B
\sim ( A \cup B ) = \sim A \cap \sim B
∼(A∪B)=∼A∩∼B ,
∼
(
A
∩
B
)
=
∼
A
∪
∼
B
\sim ( A \cap B ) = \sim A \cup \sim B
∼(A∩B)=∼A∪∼B
② Relative form :
A
−
(
B
∪
C
)
=
(
A
−
B
)
∩
(
A
−
C
)
A - (B \cup C) = ( A - B ) \cap (A - C)
A−(B∪C)=(A−B)∩(A−C) ,
A
−
(
B
∩
C
)
=
(
A
−
B
)
∪
(
A
−
C
)
A - (B \cap C) = ( A - B ) \cup (A - C)
A−(B∩C)=(A−B)∪(A−C)
6. absorptivity :
A
∪
(
A
∩
B
)
=
A
A \cup ( A \cap B ) = A
A∪(A∩B)=A ,
A
∩
(
A
∪
B
)
=
A
A \cap (A \cup B) = A
A∩(A∪B)=A
7. Law of zero :
A
∪
E
=
E
A \cup E = E
A∪E=E ,
A
∩
∅
=
∅
A \cap \varnothing = \varnothing
A∩∅=∅
8. The same thing :
A
∪
∅
=
A
A \cup \varnothing = A
A∪∅=A ,
A
∩
E
=
A
A \cap E = A
A∩E=A
( An empty set is the unit element of a union operation , The complete set is the unit element of intersection operation )
9. The law of excluded middle :
A
∪
∼
A
=
E
A \cup \sim A = E
A∪∼A=E
10. Law of contradiction :
A
∩
∼
A
=
∅
A \cap \sim A = \varnothing
A∩∼A=∅
11. Complementary law :
∼
∅
=
E
\sim \varnothing = E
∼∅=E ,
∼
E
=
∅
\sim E= \varnothing
∼E=∅
12. The law of double negation :
∼
(
∼
A
)
=
A
\sim ( \sim A ) = A
∼(∼A)=A
13. Complementary transformation law :
A
−
B
=
A
∩
∼
B
A - B = A \cap \sim B
A−B=A∩∼B
( The difference operation of sets is unnecessary , Intersection and complement operations of sets can replace difference operations )
Two 、 Generalization of set identities to set families
{
A
α
}
α
∈
S
\{ A_\alpha \}_{\alpha \in S}
{ Aα}α∈S For the set family ,
S
S
S Is the indicator set ,
α
\alpha
α It is the element in the indicator set , about
S
S
S In the collection
α
\alpha
α Elements , There is a set
A
α
A_\alpha
Aα With the corresponding ; be-all
A
α
A_\alpha
Aα Put it together , Form a family ;
B
B
B Is an arbitrary set ;
1 . Distributive law
Distributive law ① :
B
∪
(
⋂
{
A
α
}
α
∈
S
)
=
⋂
α
∈
S
(
B
∪
A
α
)
B \cup ( \bigcap \{ A_\alpha \}_{\alpha \in S} ) = \bigcap_{\alpha \in S} ( B \cup A_\alpha )
B∪(⋂{ Aα}α∈S)=α∈S⋂(B∪Aα)
Find the intersection of each set element in the set family , Then with
B
B
B Perform and calculate ; Equivalent to Set each element in the family with
B
B
B Union , Then find the intersection of each of the above union operation results ;
Distributive law ② :
B
∩
(
⋃
{
A
α
}
α
∈
S
)
=
⋃
α
∈
S
(
B
∩
A
α
)
B \cap ( \bigcup \{ A_\alpha \}_{\alpha \in S} ) = \bigcup_{\alpha \in S} ( B \cap A_\alpha )
B∩(⋃{ Aα}α∈S)=α∈S⋃(B∩Aα)
Join each set element in the set family , Then with
B
B
B Perform intersection ; Equivalent to Set each element in the family with
B
B
B Intersection , Then find the union of each of the above union operation results ;
2 . De Morgan law
De Morgan law ( absolute form ) ① :
∼
(
⋃
{
A
α
}
α
∈
S
)
=
⋂
α
∈
S
(
∼
A
α
)
\sim ( \bigcup \{ A_\alpha \}_{\alpha \in S} ) = \bigcap_{\alpha \in S} ( \sim A_\alpha )
∼(⋃{ Aα}α∈S)=α∈S⋂(∼Aα)
Generalized union of set family , Then make up ; be equal to Each set in the set family , Make up first , Then find the generalized intersection ;
De Morgan law ( absolute form ) ② :
∼
(
⋂
{
A
α
}
α
∈
S
)
=
⋃
α
∈
S
(
∼
A
α
)
\sim ( \bigcap \{ A_\alpha \}_{\alpha \in S} ) = \bigcup_{\alpha \in S} ( \sim A_\alpha )
∼(⋂{ Aα}α∈S)=α∈S⋃(∼Aα)
Generalized intersection of set families , Then make up ; be equal to Each set in the set family , Make up first , Then find the generalized union ;
De Morgan law ( Relative form ) ③ :
B
−
(
⋃
{
A
α
}
α
∈
S
)
=
⋂
α
∈
S
(
B
−
A
α
)
B - ( \bigcup \{ A_\alpha \}_{\alpha \in S} ) = \bigcap_{\alpha \in S} ( B - A_\alpha )
B−(⋃{ Aα}α∈S)=α∈S⋂(B−Aα)
B
B
B Set subtraction Generalized union of set family ( Set family generalized union be relative to aggregate
B
B
B The complement of ) ; be equal to
B
B
B Set minus each set in the set family , First find the relative complement , Then find the generalized intersection ;
De Morgan law ( Relative form ) ④ :
B
−
(
⋂
{
A
α
}
α
∈
S
)
=
⋃
α
∈
S
(
B
−
A
α
)
B - ( \bigcap \{ A_\alpha \}_{\alpha \in S} ) = \bigcup_{\alpha \in S} ( B - A_\alpha )
B−(⋂{ Aα}α∈S)=α∈S⋃(B−Aα)
B
B
B Set subtraction Generalized intersection of set families ( Set family generalized intersection be relative to aggregate
B
B
B The complement of ) ; be equal to
B
B
B Set minus each set in the set family , First find the relative complement , Then find the generalized union ;
边栏推荐
- SAP UI5 应用开发教程之一百零五 - SAP UI5 Master-Detail 布局模式的联动效果实现明细介绍
- Classes in TS
- Mila, University of Ottawa | molecular geometry pre training with Se (3) invariant denoising distance matching
- 105. SAP UI5 Master-Detail 布局模式的联动效果实现明细介绍
- 2.14 simulation summary
- 在写web项目的时候,文件上传用到了smartupload,用了new string()进行转码,但是在数据库中,还是会出现类似扑克的乱码
- [Blue Bridge Road - bug free code] pcf8591 - code analysis of AD conversion
- What can learning pytorch do?
- Wechat applet + Alibaba IOT platform + Hezhou air724ug build a serverless IOT system (III) -- wechat applet is directly connected to Alibaba IOT platform aliiot
- 第十届中国云计算大会·中国站:展望未来十年科技走向
猜你喜欢

深潜Kotlin协程(十九):Flow 概述
When writing a web project, SmartUpload is used for file upload and new string () is used for transcoding, but in the database, there will still be random codes similar to poker

Nat. Comm. | 使用Tensor-cell2cell对细胞通讯进行环境感知去卷积
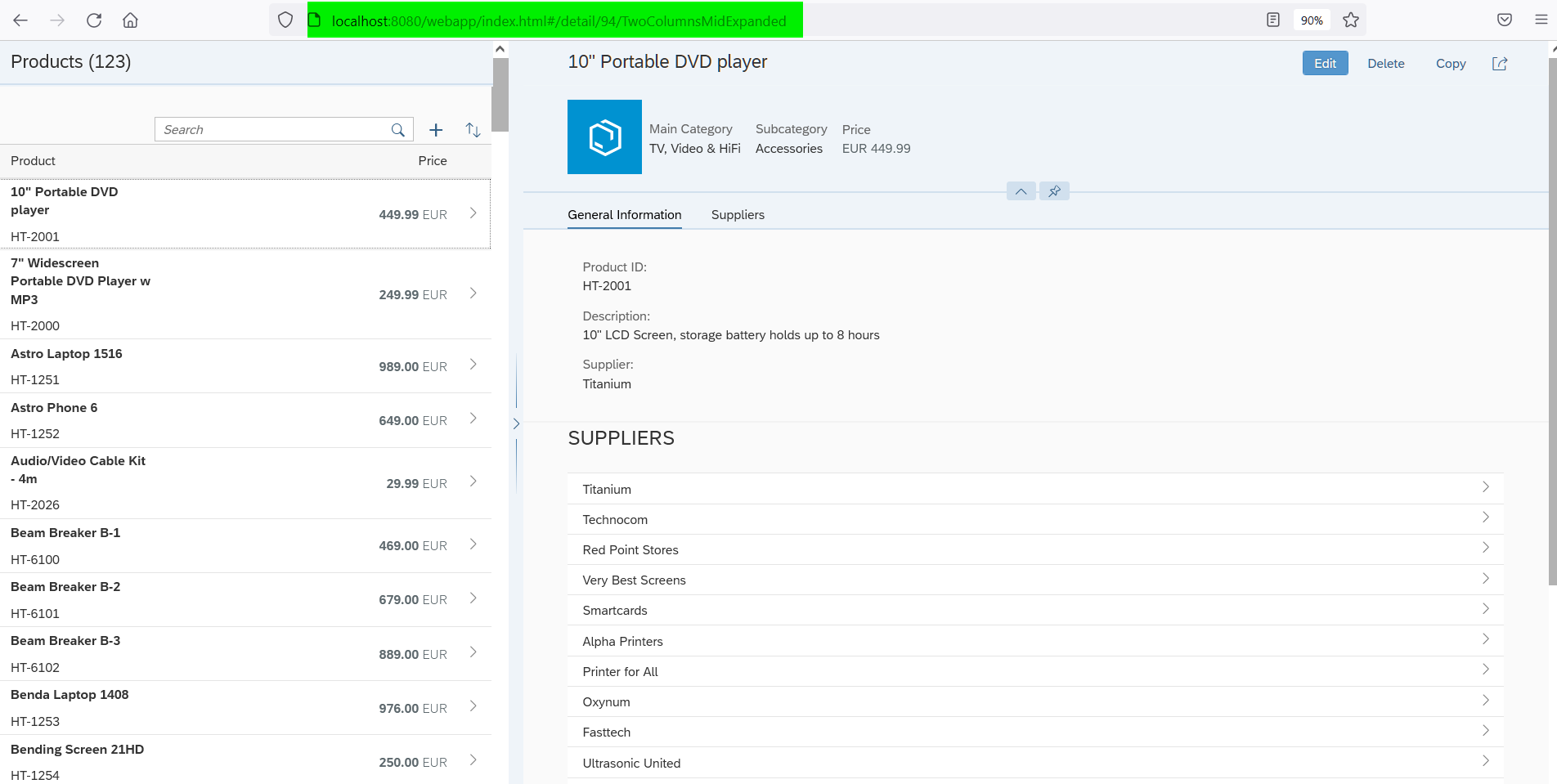
105. SAP UI5 Master-Detail 布局模式的联动效果实现明细介绍
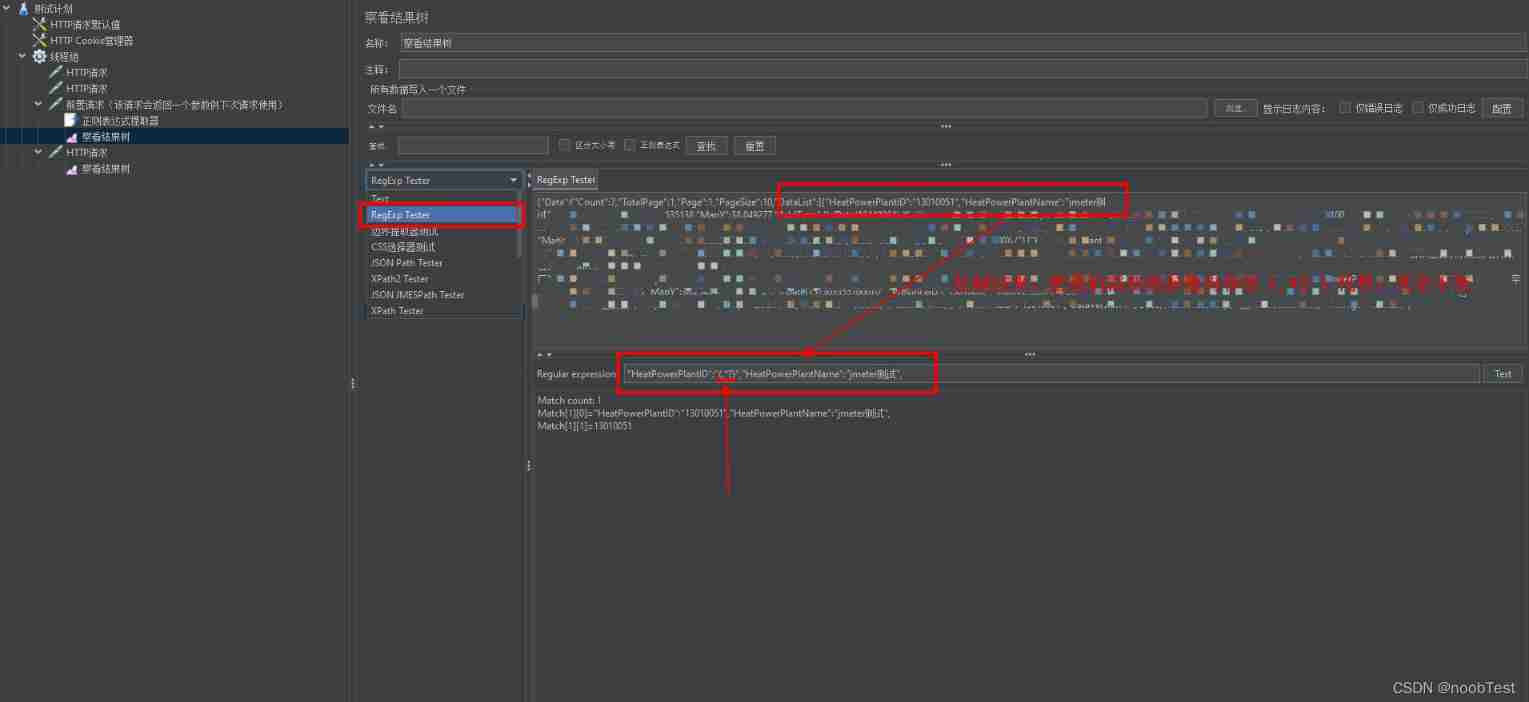
JMeter starts from zero (III) -- simple use of regular expressions

CVPR 2022 | 大連理工提出自校准照明框架,用於現實場景的微光圖像增强
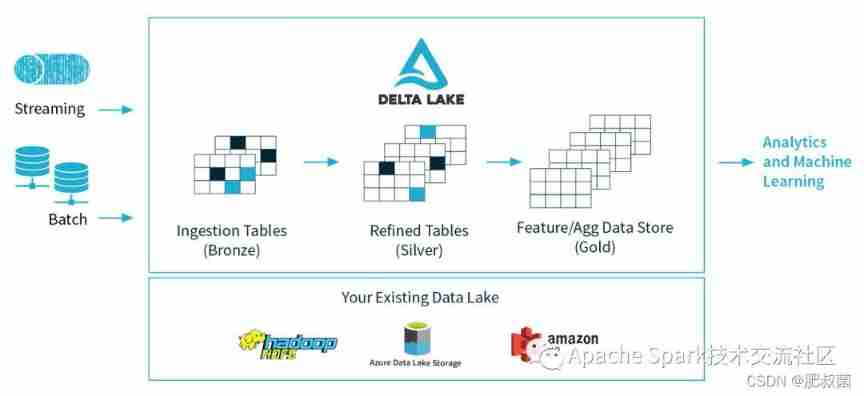
Data Lake three swordsmen -- comparative analysis of delta, Hudi and iceberg

中移物联网OneOS与OneNET入选《2021年物联网示范项目名单》
Five elements of user experience

【刷题篇】 找出第 K 小的数对距离
随机推荐
Mila, University of Ottawa | molecular geometry pre training with Se (3) invariant denoising distance matching
Is pytorch open source?
2022deepbrainchain biweekly report no. 104 (01.16-02.15)
[set theory] set concept and relationship (set represents | number set | set relationship | contains | equality | set relationship property)
Wechat applet + Alibaba IOT platform + Hezhou air724ug built with server version system analysis
Analysis of the reason why the server cannot connect remotely
[Blue Bridge Road - bug free code] pcf8591 - code analysis of AD conversion
DAPP for getting started with eth
Deep dive kotlin synergy (19): flow overview
mysql字段userid逗号分开保存按userid查询
China Mobile Internet of things oneos and onenet were selected in the list of 2021 Internet of things demonstration projects
[Blue Bridge Road -- bug free code] DS18B20 temperature reading code analysis
[set theory] set concept and relationship (set family | set family examples | multiple sets)
JS realizes lazy loading of pictures
Esp32 series (3): GPIO learning (take simple GPIO input and output, ADC, DAC as examples)
Practical operation of vim
Reflection and planning of a sophomore majoring in electronic information engineering
深潜Kotlin协程(十九):Flow 概述
Supervised pre training! Another exploration of text generation!
第十届中国云计算大会·中国站:展望未来十年科技走向