当前位置:网站首页>[mathematical logic] predicate logic (first-order predicate logic formula | example)
[mathematical logic] predicate logic (first-order predicate logic formula | example)
2022-07-03 03:48:00 【Programmer community】
List of articles
- One 、 First order predicate logic formula
- Two 、 First order predicate logic formula Example
Last blog : 【 Mathematical logic 】 Predicate logic ( Individual words | Individual domain | The predicate | Full name quantifier | There are quantifiers | Predicate formula | exercises )
One 、 First order predicate logic formula
Propositional formula : Basic proposition ( Propositional constant / Argument ) and A number of Conjunctions Form a finite length string ;
① Single Propositional argument / Propositional constant Is a proposition formula ;
② If
A
A
A Is a proposition formula , be
(
¬
A
)
(\lnot A)
(¬A) It is also a propositional formula ;
③ If
A
,
B
A,B
A,B Is a proposition formula , be
(
A
∧
B
)
,
(
A
∨
B
)
,
(
A
→
B
)
,
(
A
B
)
(A \land B) , (A \lor B), (A \to B), (A \leftrightarrow B)
(A∧B),(A∨B),(A→B),(AB) It is also a propositional formula ;
④ A limited number of times application ① ② ③ Formed symbol string Is a proposition formula ; ( Infinite times cannot )
First order predicate logic formula : stay Propositional formula On the basis of , Add a condition :
If
A
A
A It's the formula , be
∀
x
A
\forall x A
∀xA and
∃
x
A
\exist x A
∃xA Is also a formula
Related concepts of first-order predicate logic formula : With
∀
x
A
\forall x A
∀xA ,
∃
x
A
\exist x A
∃xA Take the formula as an example ;
Guide arguments :
∀
,
∃
\forall , \exist
∀,∃ After quantifier
x
x
x be called Guide arguments
Jurisdiction :
A
A
A be called The scope of the corresponding quantifier ;
Constraints appear : stay
∀
x
\forall x
∀x ,
∃
x
\exist x
∃x Jurisdiction
A
A
A in ,
x
x
x All appearances are constrained , This is called constraint occurrence ;
Free to appear : Jurisdiction
A
A
A in , It is not the argument of the constraint , Are free to appear ;
Two 、 First order predicate logic formula Example
First order predicate logic formula :
∀
x
(
F
(
x
)
→
∃
y
(
G
(
y
)
∧
H
(
x
,
y
,
z
)
)
)
\forall x ( F(x) \to \exist y ( G(y) \land H(x,y,z) ) )
∀x(F(x)→∃y(G(y)∧H(x,y,z)))
Formula interpretation : about All satisfied
F
F
F Nature
x
x
x , all There is satisfaction
G
G
G The object of nature
y
y
y , bring
x
,
y
,
z
x,y,z
x,y,z Satisfaction
H
H
H ;
∀
x
\forall x
∀x Of Jurisdiction yes
(
F
(
x
)
→
∃
y
(
G
(
y
)
∧
H
(
x
,
y
,
z
)
)
)
( F(x) \to \exist y ( G(y) \land H(x,y,z) ) )
(F(x)→∃y(G(y)∧H(x,y,z)))
∃
y
\exist y
∃y Of Jurisdiction yes
(
G
(
y
)
∧
H
(
x
,
y
,
z
)
)
)
( G(y) \land H(x,y,z) ) )
(G(y)∧H(x,y,z)))
x
,
y
x , y
x,y After the quantifier , yes Guide arguments , yes Constraints appear Argument of ;
z
z
z Not after the quantifier , yes Free to appear Argument of ;
Guide arguments Similar to the predefined Variable / Parameters , Free to appear Argument of It's equivalent to Temporary variable ,
边栏推荐
- Recursion: depth first search
- For instruction, uploading pictures and display effect optimization of simple wechat applet development
- 简易版 微信小程序开发之for指令、上传图片及展示效果优化
- Ansible简介【暂未完成(半成品)】
- 用Three.js做一個簡單的3D場景
- Compare float with 0
- Table structure of Navicat export database
- 渤、黄海的潮汐特征
- Applet get user avatar and nickname
- User value is the last word in the competition of mobile phone market
猜你喜欢
FileZilla Client下载安装
Role of JS No
Some preliminary preparations for QQ applet development: make an appointment for a development account, download and install developer tools, and create QQ applet

Message queue addition failure

pytorch开源吗?
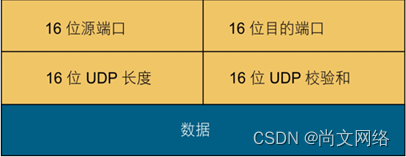
TCP, the heavyweight guest in tcp/ip model -- Kuige of Shangwen network
![Mongodb replication set [master-slave replication]](/img/2c/8030548455f45fa252062dd90e7b8b.png)
Mongodb replication set [master-slave replication]

用Three.js做一个简单的3D场景
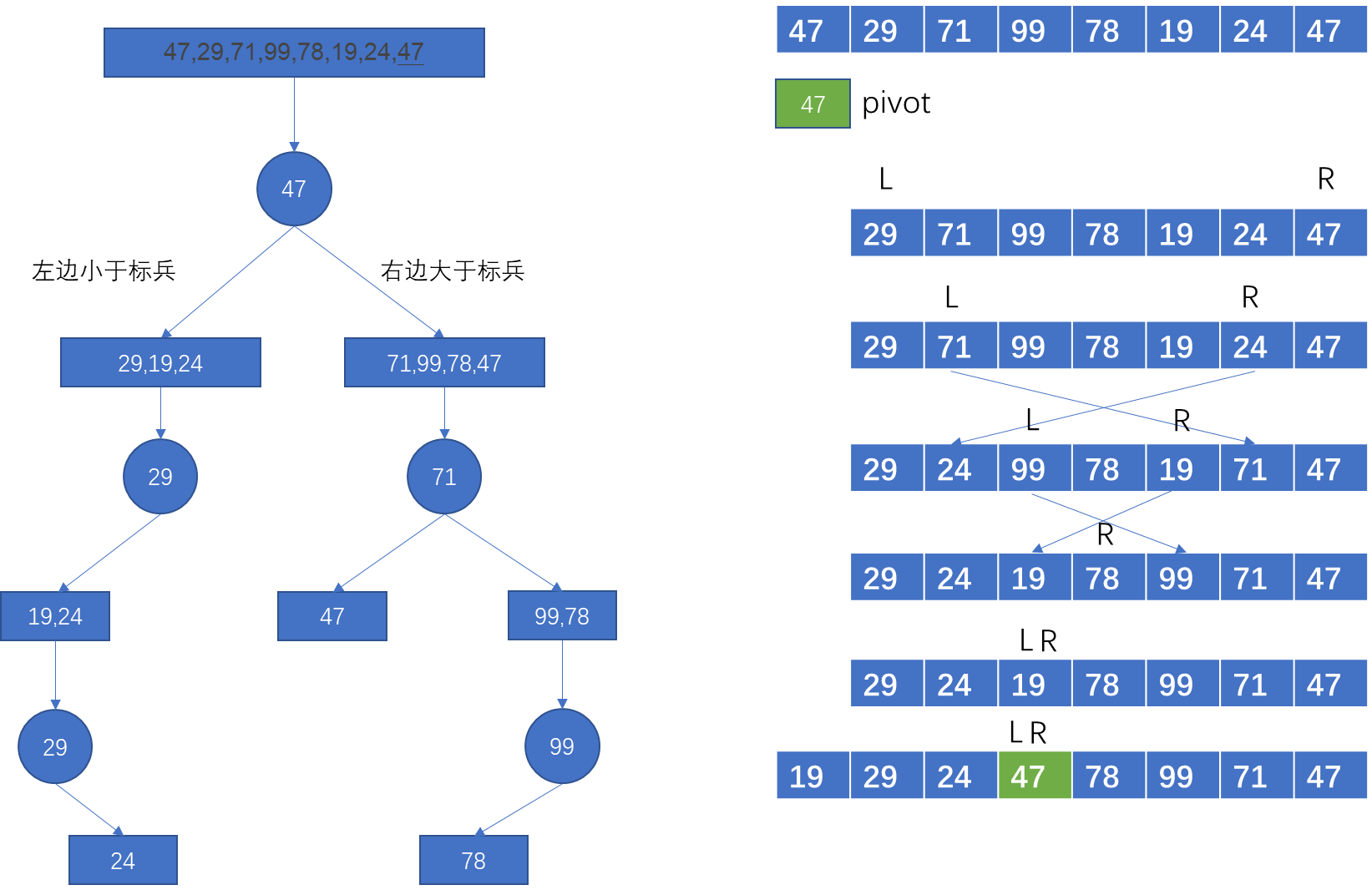
Recursion: quick sort, merge sort and heap sort

FileZilla Client下載安裝
随机推荐
MongoDB复制集【主从复制】
Web会话管理安全问题
2020-01-01t00:00:00.000000z date format conversion
[national programming] [software programming - Lecture Video] [zero foundation introduction to practical application]
Recursion: one dimensional linked lists and arrays
Simple wechat applet development page Jump, data binding, obtaining user information, obtaining user location information
[combinatorics] brief introduction to generating function (definition of generating function | Newton binomial coefficient | commonly used generating function | correlation with constant | correlation
Use of sigaction
900w+ data, from 17s to 300ms, how to operate
Positioning (relative positioning, absolute positioning, fixed positioning, Z-index) 2022-2-11
[DRM] simple analysis of DRM bridge driver call process
Role of JS No
Hi3536c v100r001c02spc040 cross compiler installation
Is pytorch open source?
静态网页 和 动态网页的区别 & WEB1.0和WEB2.0的区别 & GET 和 POST 的区别
CEPH Shangwen network xUP Nange that releases the power of data
What is pytorch? Is pytorch a software?
Captura下载安装及在Captura配置FFmpeg
Introduction à mongodb
[mathematical logic] propositional logic (judgment of the correctness of propositional logic reasoning | formal structure is eternal truth - equivalent calculus | deduction from premise - logical reas