当前位置:网站首页>L2-006 树的遍历 (25 分)
L2-006 树的遍历 (25 分)
2022-07-06 09:14:00 【%xiao Q】
题目
给定一棵二叉树的后序遍历和中序遍历,请你输出其层序遍历的序列。这里假设键值都是互不相等的正整数。
输入格式:
输入第一行给出一个正整数N(≤30),是二叉树中结点的个数。第二行给出其后序遍历序列。第三行给出其中序遍历序列。数字间以空格分隔。
输出格式:
在一行中输出该树的层序遍历的序列。数字间以1个空格分隔,行首尾不得有多余空格。
输入样例:
7
2 3 1 5 7 6 4
1 2 3 4 5 6 7
输出样例:
4 1 6 3 5 7 2
分析
这题我们得知道如何在已知二叉树的中序遍历和后序遍历的情况下建树,这里我们可以这样做,后续遍历的最后一个节点一定是根节点,然后在中序遍历中找该节点,根据中序遍历的特性可以分开左右子树,然后在递归左子树和有子树,进行同样的操作。
然后就是程序遍历,这里直接用bfs搜即可。
参考代码:
#include <iostream>
#include <cstdio>
#include <set>
#include <vector>
#include <cstring>
#include <cmath>
#include <queue>
#include <stack>
#include <algorithm>
#include <unordered_map>
#define LL long long
#define rep(i, a, b) for(int i = a; i <= b; i++)
#define reps(i, a, b) for(int i = a; i < b; i++)
#define pre(i, a, b) for(int i = b; i >= a; i--)
using namespace std;
const int N = 10010;
int pos, n;
int pre[N], in[N], post[N];
struct node
{
int l, r, w;
}T[N];
// 建树
void creat(int inl, int inr, int u)
{
if(inl > inr) return ;
// puts("hh");
// cout << u << endl;
T[u].w = post[pos--];
T[u].l = 2 * u, T[u].r = 2 * u + 1;
int mid;
for(mid = inl; mid <= inr; mid++)
if(T[u].w == in[mid]) break;
//必须先递归右子树,因为后续遍历的根节点前面一些点一定是右子树的点,
// 而我们是根据后续遍历的根节逐渐前移来去找递归的
creat(mid + 1, inr, 2 * u + 1);
creat(inl, mid - 1, 2 * u);
}
// 进行层序遍历
void bfs()
{
int idx = 0;
queue<int> q;
q.push(1);
while(q.size())
{
node t = T[q.front()];
q.pop();
if(!idx) cout << t.w;
else cout << " " << t.w;
idx++;
if(T[t.l].w != -1) q.push(t.l);
if(T[t.r].w != -1) q.push(t.r);
}
}
int main()
{
cin >> n;
rep(i, 1, n) cin >> post[i];
rep(i, 1, n) cin >> in[i];
memset(T, -1, sizeof T);
pos = n;
creat(1, n, 1);
bfs();
cout << endl;
return 0;
}
边栏推荐
- Esp8266 at+cipstart= "", "", 8080 error closed ultimate solution
- Knowledge Q & A based on Apache Jena
- Ansible practical series I_ introduction
- 自动机器学习框架介绍与使用(flaml、h2o)
- 引入了junit为什么还是用不了@Test注解
- Why is MySQL still slow to query when indexing is used?
- Remember the interview algorithm of a company: find the number of times a number appears in an ordered array
- 一键提取pdf中的表格
- 01 project demand analysis (ordering system)
- 记一次某公司面试题:合并有序数组
猜你喜欢
Deoldify project problem - omp:error 15:initializing libiomp5md dll,but found libiomp5md. dll already initialized.
La table d'exportation Navicat génère un fichier PDM
02 staff information management after the actual project
Redis的基础使用
![[recommended by bloggers] background management system of SSM framework (with source code)](/img/7f/a6b7a8663a2e410520df75fed368e2.png)
[recommended by bloggers] background management system of SSM framework (with source code)

QT creator design user interface

【博主推荐】asp.net WebService 后台数据API JSON(附源码)
Installation and use of MySQL under MySQL 19 Linux
【博主推荐】C# Winform定时发送邮箱(附源码)
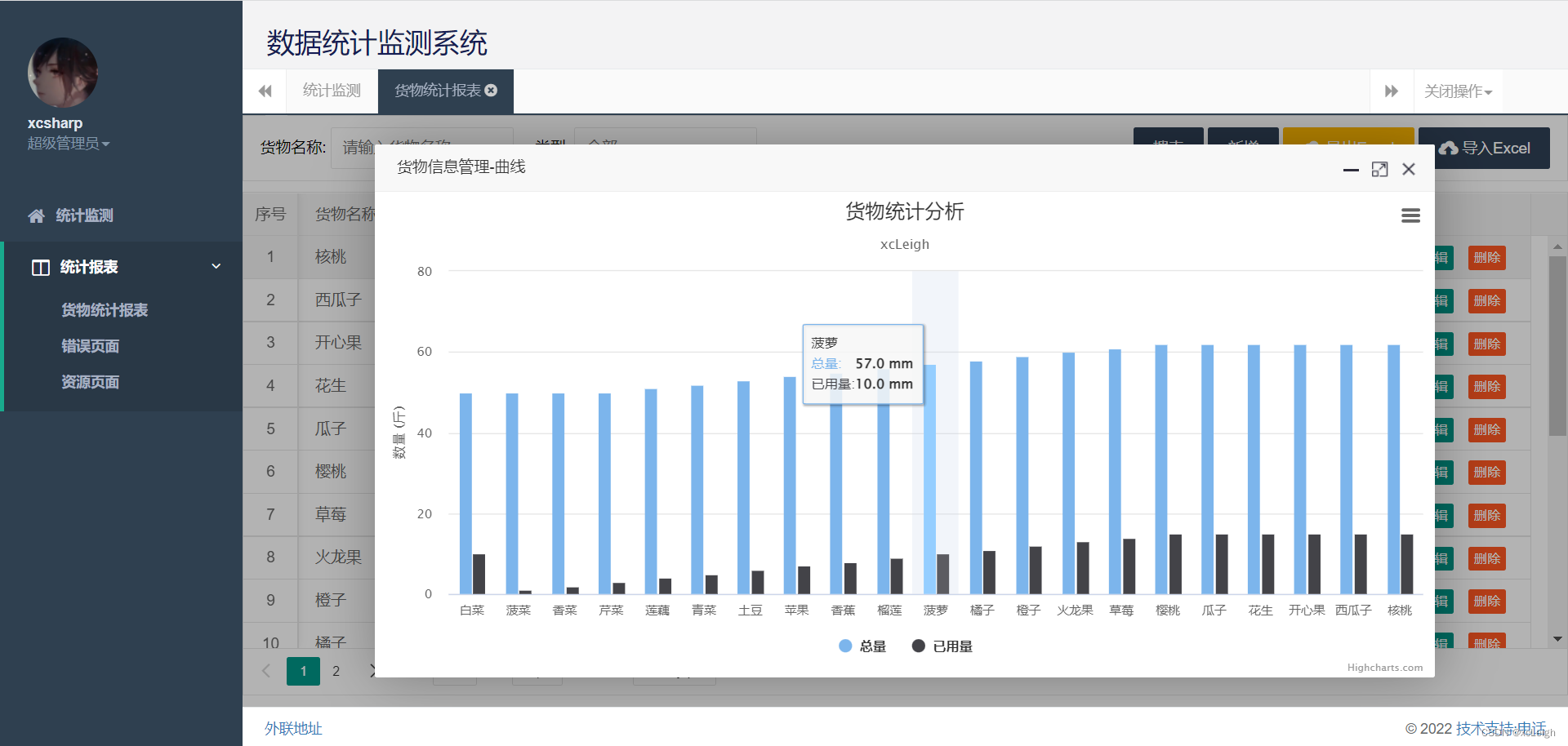
【博主推荐】C#MVC列表实现增删改查导入导出曲线功能(附源码)
随机推荐
Summary of numpy installation problems
AcWing 1298.曹冲养猪 题解
虚拟机Ping通主机,主机Ping不通虚拟机
Antlr4 uses keywords as identifiers
虚拟机Ping通主机,主机Ping不通虚拟机
[BMZCTF-pwn] 12-csaw-ctf-2016-quals hungman
【博主推荐】C#生成好看的二维码(附源码)
Some notes of MySQL
Esp8266 at+cipstart= "", "", 8080 error closed ultimate solution
数据库高级学习笔记--SQL语句
Number game
Idea import / export settings file
Unable to call numpy in pycharm, with an error modulenotfounderror: no module named 'numpy‘
QT creator support platform
Database advanced learning notes -- SQL statement
Basic use of redis
CSDN Q & a tag skill tree (V) -- cloud native skill tree
How to set up voice recognition on the computer with shortcut keys
[ahoi2009]chess Chinese chess - combination number optimization shape pressure DP
Swagger, Yapi interface management service_ SE