当前位置:网站首页>[number theory] divisor
[number theory] divisor
2022-07-06 11:04:00 【Nathan Qian】
Try division to find the divisor
subject
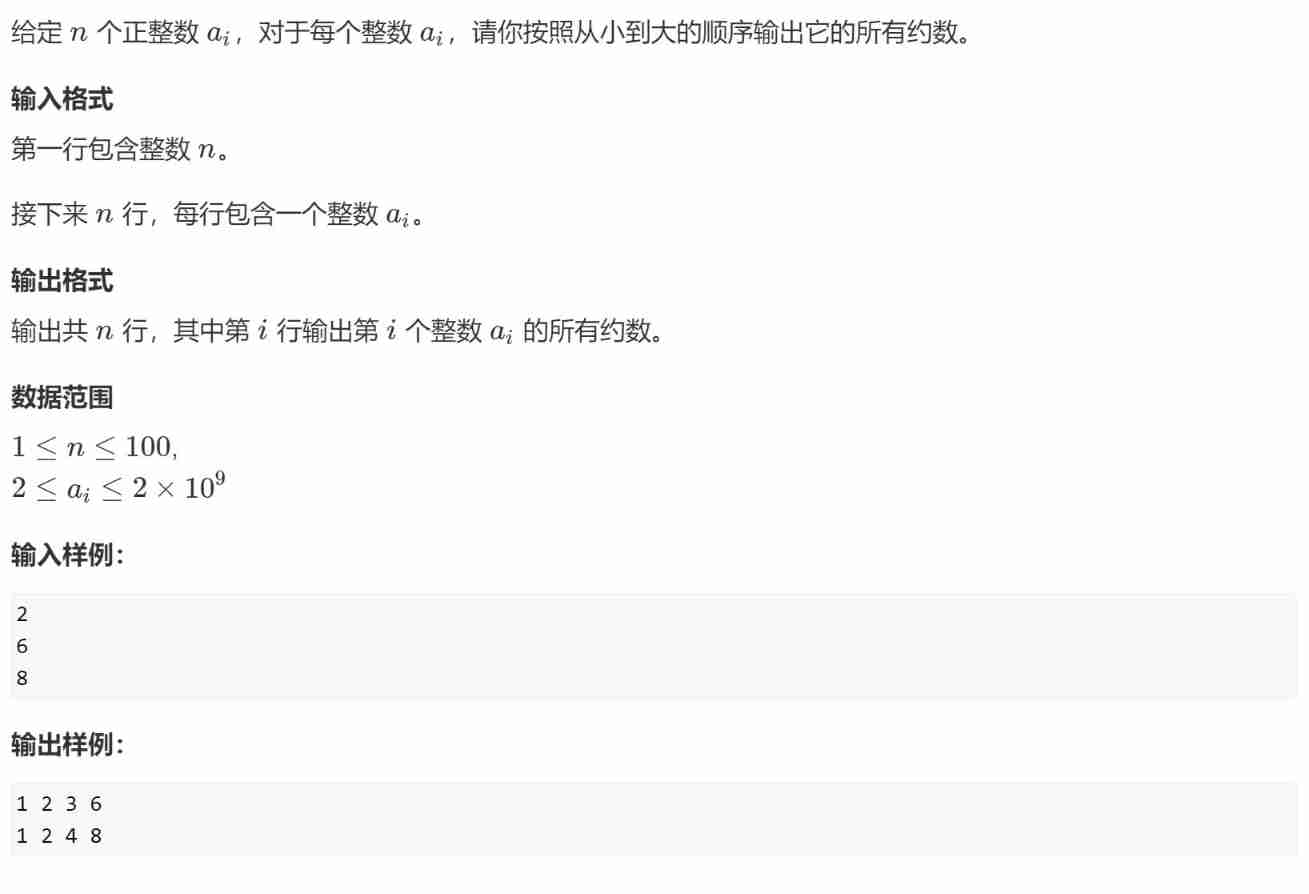
explain
- Because divisors appear in pairs , So you just need to i*i<=x
- prevent x It's a total square , One more number is recorded . Therefore, special deposit is required x/i Conditions
Code segment
#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;
vector<int>get_divisors(int x)
{
vector<int>ans;
for(int i=1;i*i<=x;i++)
{
if(x%i==0)
{
ans.push_back(i);
if(i!=x/i)ans.push_back(x/i);
}
}
sort(ans.begin(),ans.end());
return ans;
}
int main()
{
int t;
cin>>t;
while(t--)
{
int x;cin>>x;
vector<int>ans=get_divisors(x);
for(auto x:ans)cout<<x<<' ';
cout<<endl;
}
return 0;
}Find the number of divisors
subject
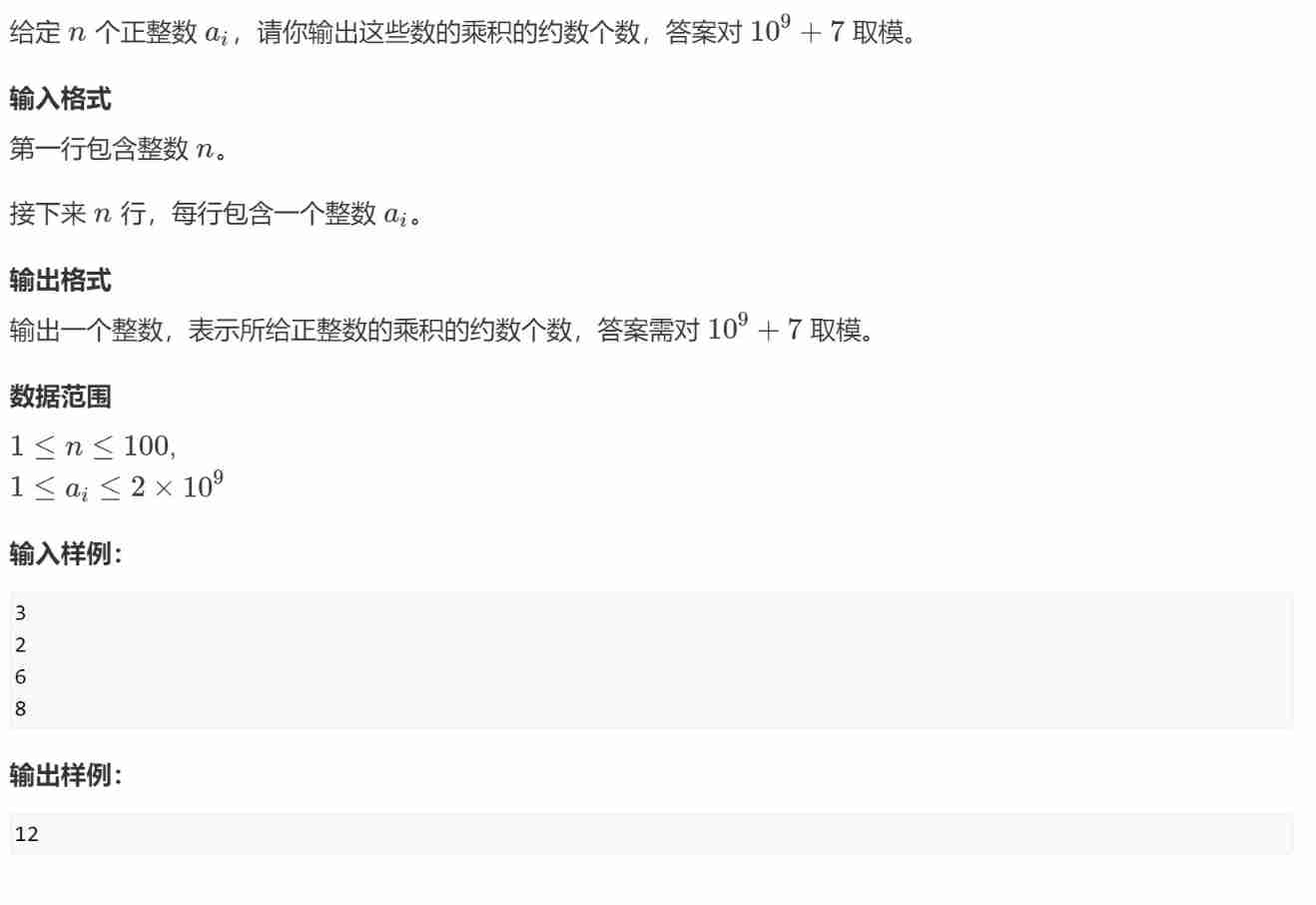
explain

- According to the above theorem , We should factorize each number , Then find the sum of prime factors
- be aware 1 Although it is a divisor , But the combination result is only 1 Kind of , So it's not in the scope
- about ans The multiplication modulus of cannot be written as ans*=x%mod, It can only be written as ans=ans*x%mod
Code segment
#include<iostream>
#include<unordered_map>
const int mod=1e9+7;
using namespace std;
unordered_map<int,int>primes;
int main()
{
int n;cin>>n;
while(n--)
{
int x;cin>>x;
for(int i=2;i*i<=x;i++)
{
if(x%i==0)
{
while(x%i==0)
{
primes[i]++;
x/=i;
}
}
}
if(x>1)primes[x]++;
}
long long ans=1;
for(auto it=primes.begin();it!=primes.end();it++)
{
ans=ans*(1+it->second)%mod;
}
cout<<ans%mod<<endl;
}The sum of the approximations
subject

explain

- Here, please a1^α1 Sum of divisors of , It is obvious that there can be algebraic theorems
- Multiplication principle , It can be understood as the sum of each power combination of each prime number
- Select a number in each bracket and multiply it to exactly equal one of the divisors
- This does not repeat the choice of accumulation , That is, the sum of approximations
- When finding the sum of divisors of prime numbers , For the accumulation of proportional series
- The simple formula is
int t( frequency ) ,x( base number ),sum( and )
while(t--)
{
sum=sum*x+1;
}
Code segment
#include<iostream>
#include<unordered_map>
const int mod=1e9+7;
using namespace std;
int main()
{
int t;cin>>t;
unordered_map<int,int>primes;
while(t--)
{
int x;cin>>x;
for(int i=2;i*i<=x;i++)
{
if(x%i==0)
{
while(x%i==0)
{
primes[i]++;
x/=i;
}
}
}
if(x>1)primes[x]++;
}
long long sum=1;
for(auto it=primes.begin();it !=primes.end();it++)
{
long long tmp=1;
int t=it->second;
while(t--)
{
tmp=(tmp*it->first+1)%mod;
}
sum=sum*tmp%mod;
// Although it can guarantee tmp No more than mod, But if sum*tmp It is likely to be greater than mod
}
cout<<sum<<endl;
}greatest common divisor
subject

explain
- Mathematical proof of Euclidean algorithm
- 【 number theory 】 Euclid algorithm _nathanqian123 The blog of -CSDN Blog
#include<iostream>
using namespace std;
int gcd(int a,int b)
{
return b==0?a:gcd(b,a%b);
}
int main()
{
int t;cin>>t;
while(t--)
{
int a,b;
cin>>a>>b;
cout<<gcd(a,b)<<endl;
}
}边栏推荐
- The virtual machine Ping is connected to the host, and the host Ping is not connected to the virtual machine
- 01项目需求分析 (点餐系统)
- CSDN question and answer module Title Recommendation task (II) -- effect optimization
- Install MySQL for Ubuntu 20.04
- C language advanced pointer Full Version (array pointer, pointer array discrimination, function pointer)
- 【博主推荐】asp.net WebService 后台数据API JSON(附源码)
- Deoldify项目问题——OMP:Error#15:Initializing libiomp5md.dll,but found libiomp5md.dll already initialized.
- Win10: how to modify the priority of dual network cards?
- TCP/IP协议(UDP)
- [untitled]
猜你喜欢
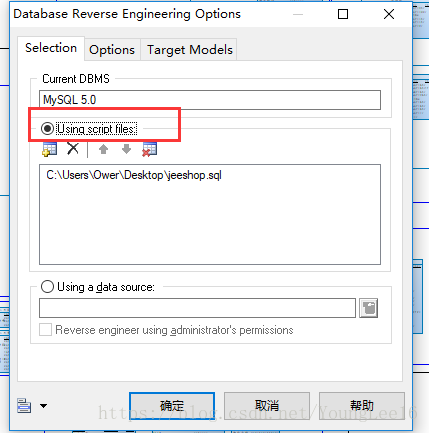
La table d'exportation Navicat génère un fichier PDM
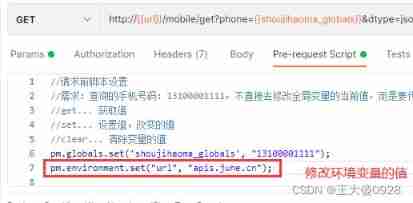
Postman uses scripts to modify the values of environment variables

Breadth first search rotten orange
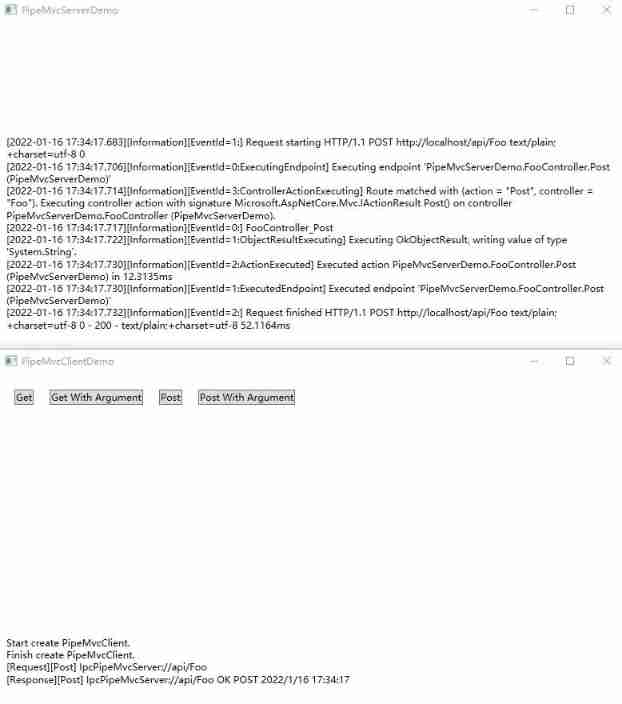
Dotnet replaces asp Net core's underlying communication is the IPC Library of named pipes
35 is not a stumbling block in the career of programmers
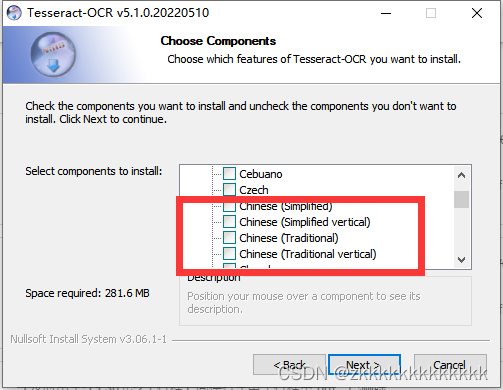
图像识别问题 — pytesseract.TesseractNotFoundError: tesseract is not installed or it‘s not in your path
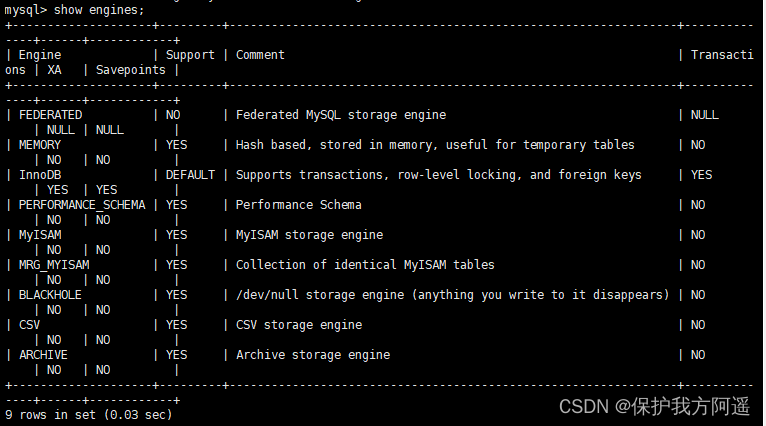
Mysql23 storage engine
Invalid global search in idea/pychar, etc. (win10)
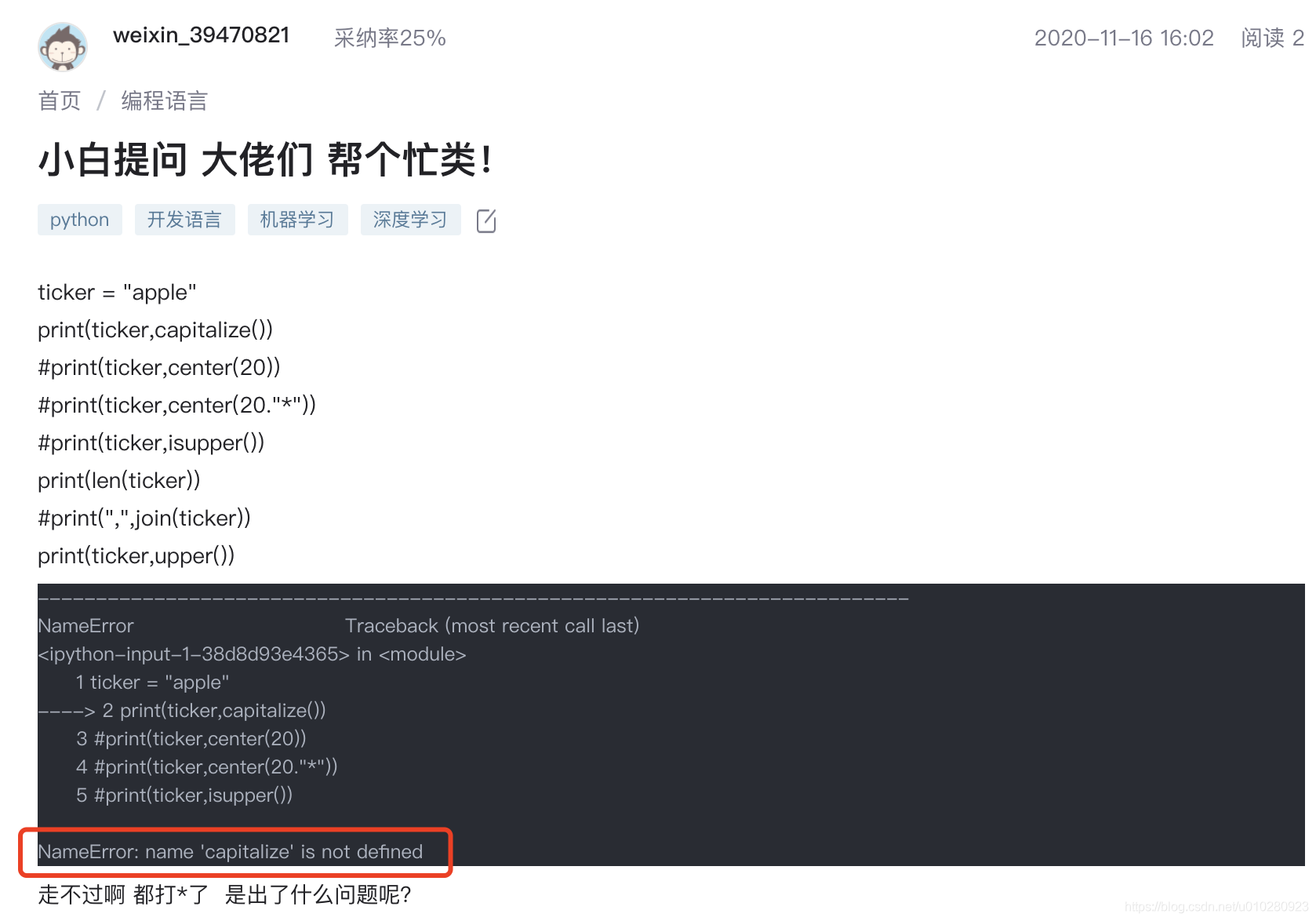
CSDN问答模块标题推荐任务(二) —— 效果优化

Why is MySQL still slow to query when indexing is used?
随机推荐
C语言标准的发展
MySQL23-存儲引擎
1. Mx6u learning notes (VII): bare metal development (4) -- master frequency and clock configuration
Postman Interface Association
[recommended by bloggers] C # generate a good-looking QR code (with source code)
CSDN问答模块标题推荐任务(二) —— 效果优化
La table d'exportation Navicat génère un fichier PDM
[recommended by bloggers] background management system of SSM framework (with source code)
Global and Chinese markets for aprotic solvents 2022-2028: Research Report on technology, participants, trends, market size and share
Deoldify项目问题——OMP:Error#15:Initializing libiomp5md.dll,but found libiomp5md.dll already initialized.
[Li Kou 387] the first unique character in the string
Windows cannot start the MySQL service (located on the local computer) error 1067 the process terminated unexpectedly
Ansible practical Series II_ Getting started with Playbook
JDBC principle
MySQL的一些随笔记录
neo4j安装教程
MySQL主从复制、读写分离
02-项目实战之后台员工信息管理
Redis的基础使用
MySQL18-MySQL8其它新特性