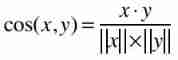Simple recommendation based on Euclidean distance

note

Minkowski distance ：

among ：

• r = 1  The formula is Manhattan distance
• r = 2  This formula is called Euclidean distance
• r = ∞  Maximal distance

*r The bigger the value is. , The difference size of a single dimension will have a greater impact on the overall distance .

 

 

Pearson correlation coefficient is used to measure the correlation between two variables

Its value is -1 to 1 Between ,1 It means a perfect match ,-1 It means completely contrary to

There is another formula , Be able to calculate the approximate value of Pearson correlation coefficient ：

Although this formula looks more complicated , And the calculation results are not very stable , There is a certain error , But its biggest advantage is , When implemented in code, you can only traverse the data once

 

 

 

What kind of similarity should be used ？

• If the data exists “ Fraction inflation ” problem , Just use Pearson correlation coefficient .
• If data comparison “ Concentrated ”, There are basically public values between variables , And these distance data are very important , Use Euclidean or Manhattan distances .
• If the data is sparse , Cosine similarity is used .

among ,“·” Sign means quantity product .“||x||” It's a vector x The mold , The formula is ：

Manhattan distance and Euclidean distance work very well with complete data , If the data is sparse , Then consider using cosine distance .

 

Use Euclidean distance to realize simple recommendation function :

# -*- coding: utf-8 -*-
"""
Created on Mon Feb 28 09:52:22 2022

@author: Knight
"""

from math import sqrt


users = {"Angelica": {"Blues Traveler": 3.5, "Broken Bells": 2.0, "Norah Jones": 4.5, "Phoenix": 5.0, "Slightly Stoopid": 1.5, "The Strokes": 2.5, "Vampire Weekend": 2.0},
         "Bill":{"Blues Traveler": 2.0, "Broken Bells": 3.5, "Deadmau5": 4.0, "Phoenix": 2.0, "Slightly Stoopid": 3.5, "Vampire Weekend": 3.0},
         "Chan": {"Blues Traveler": 5.0, "Broken Bells": 1.0, "Deadmau5": 1.0, "Norah Jones": 3.0, "Phoenix": 5, "Slightly Stoopid": 1.0},
         "Dan": {"Blues Traveler": 3.0, "Broken Bells": 4.0, "Deadmau5": 4.5, "Phoenix": 3.0, "Slightly Stoopid": 4.5, "The Strokes": 4.0, "Vampire Weekend": 2.0},
         "Hailey": {"Broken Bells": 4.0, "Deadmau5": 1.0, "Norah Jones": 4.0, "The Strokes": 4.0, "Vampire Weekend": 1.0},
         "Jordyn":  {"Broken Bells": 4.5, "Deadmau5": 4.0, "Norah Jones": 5.0, "Phoenix": 5.0, "Slightly Stoopid": 4.5, "The Strokes": 4.0, "Vampire Weekend": 4.0},
         "Sam": {"Blues Traveler": 5.0, "Broken Bells": 2.0, "Norah Jones": 3.0, "Phoenix": 5.0, "Slightly Stoopid": 4.0, "The Strokes": 5.0},
         "Veronica": {"Blues Traveler": 3.0, "Norah Jones": 5.0, "Phoenix": 4.0, "Slightly Stoopid": 2.5, "The Strokes": 3.0}
        }


#  Calculate Euclid distance 
def ouji(rating1, rating2):
    commonRating = False
    
    sum = 0
    for r1 in rating1:
        if r1 in rating2:
            sum += (rating1[r1] - rating2[r1])**2
            commonRating = True
            
    distance = sqrt(sum)
    if commonRating:
        return distance
    else:
        return -1
    

#  Get the user with the smallest Euclidean distance 
def getNearestUser(username, users):
    distances = []
    
    for user in users:
        if user != username:
            distance = ouji(users[user], users[username])
            distances.append((distance, user))
            
    distances.sort()
    return distances[0][1]


def recommend(username, users):
    nearest = getNearestUser(username, users)
    recomendations = []
    
    waitingList = users[nearest]
    doneList = users[username]
    for value in waitingList:
        if not value in doneList:
            recomendations.append((value, waitingList[value]))
            
    return recomendations
    

print( recommend("Chan", users))
# >>> [('The Strokes', 2.5), ('Vampire Weekend', 2.0)]

print( recommend("Jordyn", users))
# >>> [('Blues Traveler', 3.0)]