C＃，数值计算（Numerical Recipes in C＃），线性代数方程的求解，Gauss-Jordan消去法，源代码

 

《Numerical Recipes》原文摘要：

Gauss-Jordan elimination is probably the way you learned to solve linear equa- tions in high school. (You may have learned it as “Gaussian elimination,” but, strictly speaking, that term refers to the somewhat different technique discussed in §2.2.) The basic idea is to add or subtract linear combinations of the given equations until each equation contains only one of the unknowns, thus giving an immediate solution. You might also have learned to use the same technique for calculating the inverse of a matrix.

For solving sets of linear equations, Gauss-Jordan elimination produces both the solution of the equations for one or more right-hand side vectors b, and also the matrix inverse A—1. However, its principal deficiencies are (i) that it requires all the right-hand sides to be stored and manipulated at the same time, and (ii) that when the inverse matrix is not desired, Gauss-Jordan is three times slower than the best alternative technique for solving a single linear set (§2.3). The method’s principal strength is that it is as stable as any other direct method, perhaps even a bit more stable when full pivoting is used (see §2.1.2).

For inverting a matrix, Gauss-Jordan elimination is about as efficient as any other direct method. We know of no reason not to use it in this application if you are sure that the matrix inverse is what you really want.

You might wonder about deficiency (i) above: If we are getting the matrix in- verse anyway, can’t we later let it multiply a new right-hand side to get an additional solution? This does work, but it gives an answer that is very susceptible to roundoff error and not nearly as good as if the new vector had been included with the set of right-hand side vectors in the first instance.

Thus, Gauss-Jordan elimination should not be your method of first choice for solving linear equations. The decomposition methods in §2.3 are better. Why do we discuss Gauss-Jordan at all? Because it is straightforward, solid as a rock, and a good place for us to introduce the important concept of pivoting which will also

be important for the methods described later. The actual sequence of operations performed in Gauss-Jordan elimination is very closely related to that performed by the routines in the next two sections.

凑字数的机器翻译译文：

高斯-乔丹消去法可能是你在高中学习求解线性方程的方法。（您可能已经将其理解为“高斯消元法”，但严格来说，该术语指的是§2.2中讨论的有所不同的技术。）基本思想是添加或减去给定方程的线性组合，直到每个方程只包含一个未知数，从而立即给出解。您可能还学会了使用相同的技术来计算矩阵的逆。

对于求解线性方程组，高斯-乔丹消元法生成一个或多个右侧向量b的方程解，以及矩阵逆A-1。然而，其主要缺陷是（i）它要求同时存储和操作所有右侧，以及（ii）当不需要逆矩阵时，Gauss-Jordan比求解单个线性集的最佳替代技术慢三倍（§2.3）。该方法的主要优点是，它与任何其他直接方法一样稳定，当使用完全旋转时，甚至可能更稳定一点（见§2.1.2）。

对于矩阵求逆，高斯-约当消元法与任何其他直接方法一样有效。如果您确信矩阵逆是您真正想要的，那么我们没有理由不在这个应用程序中使用它。

你可能会想知道上面的缺陷（i）：如果我们得到的是相反的矩阵，我们不能稍后让它乘以一个新的右手边来得到一个额外的解决方案吗？这确实可行，但它给出的答案很容易受到舍入误差的影响，并且不如新向量在第一个实例中包含在右侧向量集中那样好。

因此，高斯-乔丹消元法不应成为求解线性方程组的首选方法。§2.3中的分解方法更好。为什么我们要讨论高斯·乔丹？因为它简单明了，坚固如磐石，是我们引入旋转这一重要概念的好地方

对于后面描述的方法很重要。在高斯-乔丹消元法中执行的实际操作序列与接下来两节中的例程执行的操作序列密切相关。

列增广矩阵的消除

为了清楚起见，并避免写出无尽的椭圆（），我们将只写出四个方程和四个未知数的情况下的方程，并且具有三个事先已知的不同右侧向量。您可以编写更大的矩阵，并以完全类似的方式将方程扩展到具有M组右侧向量的N个矩阵的情况。当然，下文§2.1.2中实施的例行程序是通用的。

 

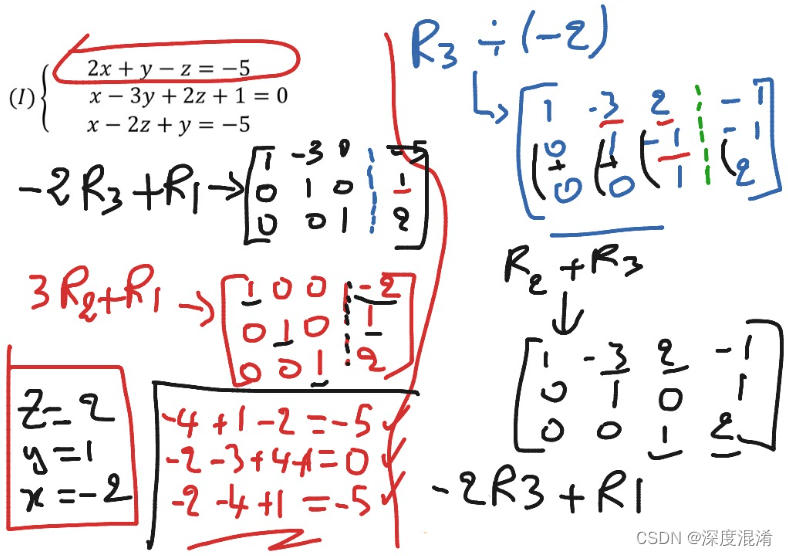
选主元

In “Gauss-Jordan elimination with no pivoting,” only the second operation in the above list is used. The zeroth row is divided by the element a00 (this being a trivial linear combination of the zeroth row with any other row — zero coefficient for the other row). Then the right amount of the zeroth row is subtracted from each other row to make all the remaining ai0’s zero. The zeroth column of A now agrees with the identity matrix. We move to column 1 and divide row 1 by a11, then subtract the right amount of row 1 from rows 0, 2, and 3, so as to make their entries in column 1 zero. Column 1 is now reduced to the identity form. And so on for columns 2 and 3. As we do these operations to A, we of course also do the corresponding operations to the b’s and to 1 (which by now no longer resembles the identity matrix in any way!). Obviously we will run into trouble if we ever encounter a zero element on the (then current) diagonal when we are going to divide by the diagonal element. (The element that we divide by, incidentally, is called the pivot element or pivot.) Not so obvious, but true, is the fact that Gauss-Jordan elimination with no pivoting (no use of the first or third procedures in the above list) is numerically unstable in the presence of any roundoff error, even when a zero pivot is not encountered. You must never do
Gauss-Jordan elimination (or Gaussian elimination; see below) without pivoting!
So what is this magic pivoting? Nothing more than interchanging rows (partial pivoting) or rows and columns (full pivoting), so as to put a particularly desirable element in the diagonal position from which the pivot is about to be selected. Since we don’t want to mess up the part of the identity matrix that we have already built up, we can choose among elements that are both (i) on rows below (or on) the one that is about to be normalized, and also (ii) on columns to the right (or on) the column we are about to eliminate. Partial pivoting is easier than full pivoting, because we don’t have to keep track of the permutation of the solution vector. Partial pivoting makes available as pivots only the elements already in the correct column. It turns out that partial pivoting is “almost” as good as full pivoting, in a sense that can be made mathematically precise, but which need not concern us here (for discussion and references, see [1]). To show you both variants, we do full pivoting in the routine in this section and partial pivoting in §2.3.
We have to state how to recognize a particularly desirable pivot when we see one. The answer to this is not completely known theoretically. It is known, both theoretically and in practice, that simply picking the largest (in magnitude) available element as the pivot is a very good choice. A curiosity of this procedure, however, is that the choice of pivot will depend on the original scaling of the equations. If we take the third linear equation in our original set and multiply it by a factor of a million, it is almost guaranteed that it will contribute the first pivot; yet the underlying solution

of the equations is not changed by this multiplication! One therefore sometimes sees routines which choose as pivot that element which would have been largest if the original equations had all been scaled to have their largest coefficient normalized to unity. This is called implicit pivoting. There is some extra bookkeeping to keep track of the scale factors by which the rows would have been multiplied. (The routines in
§2.3 include implicit pivoting, but the routine in this section does not.)
Finally, let us consider the storage requirements of the method. With a little reflection you will see that at every stage of the algorithm, either an element of A is predictably a one or zero (if it is already in a part of the matrix that has been reduced to identity form) or else the exactly corresponding element of the matrix that started as 1 is predictably a one or zero (if its mate in A has not been reduced to the identity form). Therefore the matrix 1 does not have to exist as separate storage: The matrix inverse of A is gradually built up in A as the original A is destroyed. Likewise, the solution vectors x can gradually replace the right-hand side vectors b and share the same storage, since after each column in A is reduced, the corresponding row entry in the b’s is never again used.
Here is a routine that does Gauss-Jordan elimination with full pivoting, replac- ing its input matrices by the desired answers. Immediately following is an over- loaded version for use when there are no right-hand sides, i.e., when you want only the matrix inverse.

在“无旋转的高斯-乔丹消元法”中，仅使用上述列表中的第二个运算。第零行除以元素a00（这是第零行与任何其他行的平凡线性组合-另一行的零系数）。然后从另一行中减去第0行的正确数量，使所有剩余的ai0为零。现在，A的第0列与单位矩阵一致。我们移动到第1列，将第1行除以a11，然后从第0、2和3行中减去适当数量的第1行，使其在第1列中的条目为零。第1列现在简化为标识形式。对于第2列和第3列，依此类推。当我们对A进行这些运算时，我们当然也对b和1进行相应的运算（到目前为止，它们不再以任何方式类似于单位矩阵！）。显然，当我们要除以对角线元素时，如果我们在（当时的）对角线上遇到零元素，我们会遇到麻烦。（顺便提一下，我们除以的元素称为枢轴元素或枢轴。）不太明显但真实的事实是，在存在任何舍入误差的情况下，即使没有遇到零枢轴，不带枢轴的高斯-乔丹消元法（不使用上述列表中的第一个或第三个过程）在数值上是不稳定的。你绝对不能这样做

高斯-乔丹消去法（或高斯消去法；见下文）无需旋转！

那么这个神奇的旋转是什么呢？只需交换行（部分旋转）或行和列（完全旋转），以便将特别需要的元素放置在将要选择轴的对角位置。因为我们不想弄乱我们已经建立的单位矩阵的一部分，我们可以在以下元素中进行选择：（i）在即将被规范化的行的下面（或上面），以及（ii）在右侧的列上（或在我们将要消除的列上）。部分旋转比完全旋转容易，因为我们不必跟踪解向量的排列。部分旋转仅使已在正确列中的元素可用作轴。事实证明，部分旋转“几乎”与完全旋转一样好，从某种意义上说，可以在数学上精确，但这不需要我们在这里关注（有关讨论和参考，请参阅[1]）。为了向你们展示这两种变体，我们在本节的例程中进行了完全旋转，在§2.3中进行了部分旋转。

我们必须说明，当我们看到一个特别需要的轴时，如何识别它。这个问题的答案在理论上并不完全清楚。理论上和实践中都知道，简单地选取最大（数量级）可用元素作为轴心是一个非常好的选择。然而，这个过程的一个奇怪之处是，轴的选择将取决于方程的原始比例。如果我们在原始集合中取第三个线性方程，将其乘以一百万因子，几乎可以保证它将贡献第一个枢轴；然而，潜在的解决方案

这个乘法不会改变方程的！因此，人们有时会看到一些例程选择一个元素作为轴心，如果原始方程都按比例缩放，使其最大系数归一化为一，则该元素将是最大的。这称为隐式旋转。有一些额外的簿记来跟踪行乘以的比例因子。（中的例程

§2.3包括隐式旋转，但本节中的例程不包括。）

最后，让我们考虑该方法的存储要求。稍加思考，你会发现，在算法的每个阶段，a的一个元素都可以预测为1或0（如果它已经在矩阵的一部分中，该部分已简化为单位形式），或者从1开始的矩阵的完全对应的元素可以预测为1或0（如果其在a中的配对尚未简化为单位形式）。因此，矩阵1不必作为单独的存储器存在：随着原始A的破坏，A的矩阵逆在A中逐渐建立。同样，解向量x可以逐渐替换右侧向量b并共享相同的存储，因为在减少A中的每列之后，不再使用b中的相应行条目。

这里有一个例程，它使用全旋转进行高斯-乔丹消元，用所需的答案替换其输入矩阵。紧随其后的是一个重载版本，用于没有右手边时，即只需要矩阵逆时。

 

源程序（POWER BY 315SOFT.COM）：

using System;

namespace Legalsoft.Truffer
{
    /// <summary>
    /// Gauss-Jordan decomposition - PTC
    /// Linear equation solution by Gauss-Jordan elimination.
    /// The input matrix is a[0..n - 1][0..n - 1]. b[0..n - 1][0..m - 1] is
    /// input containing the m right-hand side vectors.On output,
    /// a is replaced by its matrix inverse, and b is replaced by
    /// the corresponding set of solution vectors.
    /// </summary>
    public class GaussJordan
    {
        public GaussJordan() { }

        public static void gaussj(double[,] a, double[,] b)
        {
            int n = a.GetLength(0);
            int m = b.GetLength(1);

            // These integer arrays are used for bookkeeping on the pivoting
            int[] indxc = new int[n];
            int[] indxr = new int[n];
            int[] ipiv = new int[n];

            int icol = 0;
            int irow = 0;
            for (int j = 0; j < n; j++)
            {
                ipiv[j] = 0;
            }
            // This is the main loop over the columns to be reduced.
            for (int i = 0; i < n; i++)
            {
                // This is the outer loop of the search for a pivot element.
                double big = 0.0;
                for (int j = 0; j < n; j++)
                {
                    if (ipiv[j] != 1)
                    {
                        for (int k = 0; k < n; k++)
                        {
                            if (ipiv[k] == 0)
                            {
                                if (Math.Abs(a[j, k]) >= big)
                                {
                                    big = Math.Abs(a[j, k]);
                                    irow = j;
                                    icol = k;
                                }
                            }
                        }
                    }
                }
                ++(ipiv[icol]);
                // We now have the pivot element, so we interchange rows, if needed, to put the pivot
                // element on the diagonal.The columns are not physically interchanged, only relabeled:
                // indxc[i], the column of the .i C 1 / th pivot element, is the.i C 1 / th column that is
                // reduced, while indxr[i] is the row in which that pivot element was originally located.
                // If indxr[i] or indxc[i], there is an implied column interchange. With this form of
                // bookkeeping, the solution b's will end up in the correct order, and the inverse matrix
                // will be scrambled by columns.
                if (irow != icol)
                {
                    for (int l = 0; l < n; l++)
                    {
                        Globals.SWAP(ref a[irow, l],ref a[icol, l]);
                    }
                    for (int l = 0; l < m; l++)
                    {
                        Globals.SWAP(ref b[irow, l],ref b[icol, l]);
                    }
                }
                // We are now ready to divide the pivot row by the
                // pivot element, located at irow and icol.
                indxr[i] = irow;
                indxc[i] = icol;
                //if (a[icol, icol] == 0.0)
                if (Math.Abs(a[icol, icol]) <= float.Epsilon)
                {
                    throw new Exception("gaussj: Singular Matrix");
                }
                double pivinv = 1.0 / a[icol, icol];
                a[icol, icol] = 1.0;
                for (int l = 0; l < n; l++)
                {
                    a[icol, l] *= pivinv;
                }
                for (int l = 0; l < m; l++)
                {
                    b[icol, l] *= pivinv;
                }
                // Next, we reduce the rows..., except for the pivot one, of course.
                for (int ll = 0; ll < n; ll++)
                {
                    if (ll != icol)
                    {
                        double dum = a[ll, icol];
                        a[ll, icol] = 0.0;
                        for (int l = 0; l < n; l++)
                        {
                            a[ll, l] -= a[icol, l] * dum;
                        }
                        for (int l = 0; l < m; l++)
                        {
                            b[ll, l] -= b[icol, l] * dum;
                        }
                    }
                }
            }
            for (int l = n - 1; l >= 0; l--)
            {
                if (indxr[l] != indxc[l])
                {
                    for (int k = 0; k < n; k++)
                    {
                        Globals.SWAP(ref a[k, indxr[l]],ref a[k, indxc[l]]);
                    }
                }
            }
        }

        /// <summary>
        /// Overloaded version with no right-hand sides. Replaces a by its inverse.
        /// </summary>
        /// <param name="a"></param>
        public static void gaussj(double[,] a)
        {
            double[,] b = new double[a.GetLength(0), a.GetLength(1)];
            gaussj( a,  b);
        }

    }
}