当前位置:网站首页>位运算(Bit Operation)
位运算(Bit Operation)
2022-07-07 21:50:00 【Yake1965】
位运算(Bit Operation)
- [136. 只出现一次的数字](https://leetcode-cn.com/problems/single-number/)
- [67. 二进制求和](https://leetcode-cn.com/problems/add-binary/)
- [137. 只出现一次的数字 II](https://leetcode-cn.com/problems/single-number-ii/)
- [190. 颠倒二进制位](https://leetcode-cn.com/problems/reverse-bits/)
- [191. 位1的个数](https://leetcode-cn.com/problems/number-of-1-bits/)
- [231. 2 的幂](https://leetcode-cn.com/problems/power-of-two/)
- [260. 只出现一次的数字 III](https://leetcode-cn.com/problems/single-number-iii/)
- [268. 丢失的数字](https://leetcode-cn.com/problems/missing-number/)
- [318. 最大单词长度乘积](https://leetcode-cn.com/problems/maximum-product-of-word-lengths/)
- [389. 找不同](https://leetcode-cn.com/problems/find-the-difference/)
- [397. 整数替换](https://leetcode-cn.com/problems/integer-replacement/)
- [405. 数字转换为十六进制数](https://leetcode-cn.com/problems/convert-a-number-to-hexadecimal/)
- [458. 可怜的小猪](https://leetcode-cn.com/problems/poor-pigs/)
- [476. 数字的补数](https://leetcode-cn.com/problems/number-complement/submissions/)
- [剑指 Offer II 003. 前 n 个数字二进制中 1 的个数](https://leetcode.cn/problems/w3tCBm/)
- [89. 格雷编码](https://leetcode-cn.com/problems/gray-code/)
136. 只出现一次的数字
class Solution {
public int singleNumber(int[] nums) {
int res = 0;
for (Integer i : nums) res ^= i;
return res;
}
}
67. 二进制求和
方法一:模拟
class Solution:
def addBinary(self, a: str, b: str) -> str:
m, n, res, carry = len(a), len(b), [], 0
x = max(m, n)
for i in range(-1, -x-1, -1):
# 按位求和 + 进位,和 2 的余数为当前位的结果,和 2 取商为进位。
carry += (int(a[i]) if -i <= m else 0) + (int(b[i]) if -i <= n else 0)
res.append(str(carry % 2))
carry //= 2
if carry > 0: # 添加进位
res.append('1')
return ''.join(res[::-1])
# return bin(int(a, 2) + int(b, 2))[2:]
# return '{:b}'.format(int(a, 2) + int(b, 2))
方法二:位运算
如果不允许使用加减乘除,则可以使用位运算替代上述运算中的一些加减乘除的操作。
class Solution:
def addBinary(self, a, b) -> str:
x, y = int(a, 2), int(b, 2)
while y:
answer = x ^ y
carry = (x & y) << 1
x, y = answer, carry
return bin(x)[2:]
137. 只出现一次的数字 II
方法一:统计每一个二进制位
使用位运算 (x >> i) & 1 得到 x 的第 i 个二进制位,并将它们相加再对 3 取余,得到的结果一定为 0 或 1,即为答案的第 i 个二进制位。
需要注意的是,如果使用的语言对「有符号整数类型」和「无符号整数类型」没有区分,那么可能会得到错误的答案。这是因为「有符号整数类型」(即 int 类型)的第 31 个二进制位(即最高位)是补码意义下的符号位,对应着 − 2 31 -2^{31} −231 ,而「无符号整数类型」由于没有符号,第 31 个二进制位对应着 2 31 2^{31} 231 。Python 中需要对最高位进行特殊判断。
class Solution:
def singleNumber(self, nums: List[int]) -> int:
ans = 0
for i in range(32):
total = sum((num >> i) & 1 for num in nums)
if total % 3:
# Python 这里对于最高位需要特殊判断
if i == 31:
ans -= (1 << i)
else:
ans |= (1 << i)
return ans
190. 颠倒二进制位
方法一:逐位颠倒
将 n 视作一个长为 32 的二进制串,从低位往高位枚举 n 的每一位,将其倒序添加到翻转结果 rev \textit{rev} rev 中。
每枚举一位就将 n 右移一位,这样当前 n 的最低位就是要枚举的比特位。当 n 为 0 时即可结束循环。
class Solution:
def reverseBits(self, n: int) -> int:
# rev = 0
# for i in range(32):
# if n != 0:
# # n 的二进制末尾数字,拼接到 res 的开头,移动的是 n 的末尾数字。
# rev |= (n & 1) << (31 - i)
# n >>= 1
# return rev
res = 0
for i in range(32):
# res 左移,把 n 的二进制末尾数字,拼接到结果 res 的末尾。然后 n 右移。
res = (res << 1) | (n & 1)
n >>= 1
return res
191. 位1的个数
在 Python 语言中,使用 bin() 函数可以得到一个整数的二进制字符串。
一、库函数
class Solution(object):
def hammingWeight(self, n):
return bin(n).count("1")
二、右移 32 次
n & 1 得到二进制末尾数字;把 n 右移 1 位,直至结束。
class Solution(object):
def hammingWeight(self, n):
res = 0
while n:
res += n & 1
n >>= 1
return res
231. 2 的幂
class Solution:
def isPowerOfTwo(self, n: int) -> bool:
return not n & (n - 1) and n > 0
return n & (-n) == n
260. 只出现一次的数字 III
def singleNumber(self, nums: List[int]) -> List[int]:
xor = 0
for i in nums:
xor ^= i
lb = xor & -xor # 最右侧 1,用于分组。
x = y = 0
for i in nums:
if lb & i:
x ^= i
else:
y ^= i
return [x, y]
268. 丢失的数字
class Solution:
def missingNumber(self, nums: List[int]) -> int:
## 方法一:排序
# n = len(nums)
# nums.sort()
# for i in range(n):
# if nums[i] != i:
# return i
# return n
## 方法二:哈希表
# hash = set(nums)
# for i in range(len(nums) + 1):
# if i not in hash:
# return i
## 方法三:差
# return sum(range(len(nums) + 1)) - sum(nums)
# return (n := len(nums)) * (n + 1) // 2 - sum(nums)
## 方法四:异或
res = 0
for i, num in enumerate(nums):
res ^= i ^ num
res ^= len(nums)
return res
318. 最大单词长度乘积
words[i] 用一个32 位二进制的数字表示,二进制位第 [0, 25] 位,分别对应 [a, z],利用位运算的判断两个字符 words[i] 和 words[j] 是否有公共字母。
转换: abd => 00000…1011 => 11(10进制的11)
判断公共字母: abd & b => 1011 & 0010 != 0
方法一:set
class Solution:
def maxProduct(self, words: List[str]) -> int:
s = [set(w) for w in words]
ans, n = 0, len(words)
for i in range(n):
for j in range(i + 1, n):
if not s[i] & s[j]:
ans = max(ans, len(words[i]) * len(words[j]))
return ans
方法二:位运算
class Solution:
def maxProduct(self, words: List[str]) -> int:
res, n = 0, len(words)
wordArr = [0] * n
for i, word in enumerate(words):
for ch in set(word):
wordArr[i] |= (1 << (ord(ch)-ord('a')))
for i in range(n):
for j in range(i + 1, n):
if (wordArr[i] & wordArr[j]) == 0:
res = max(res, len(words[i]) * len(words[j]))
return res
## reduce 列表推导式
masks = [reduce(lambda a, b: a | (1 << (ord(b) - ord('a'))), word, 0) for word in words]
return max((len(x[1]) * len(y[1]) for x, y in product(zip(masks, words), repeat=2) if x[0] & y[0] == 0), default=0)
class Solution:
def maxProduct(self, words: List[str]) -> int:
def hashset(word):
# 用 32 位二进制数表示 word,也就是将 字符串影射 到 数字
# | 只计算不重复字母的和,sum 是所有字母的和,"abc" 和 "aaac" sum 一样都是 7
return sum(1 << (ord(c) - ord('a')) for c in set(word))
d, ans = defaultdict(int), 0
for w in words:
h = hashset(w)
if d[h] < len(w):
for other in d:
if not other & h:
ans = max(ans, d[other] * len(w))
d[h] = len(w)
return ans
389. 找不同
方法一:计数
class Solution:
def findTheDifference(self, s: str, t: str) -> str:
d = {
}
for c in s:
d[c] = d.get(c, 0) + 1
for c in t:
d[c] = d.get(c, 0) - 1
if d[c] < 0:
return c
class Solution:
def findTheDifference(self, s: str, t: str) -> str:
d = {
}
for c in s + t:
d[c] = d.get(c, 0) + 1
return [x for x in d if d[x]%2][-1]
方法二:求和
class Solution:
def findTheDifference(self, s: str, t: str) -> str:
return chr(sum(ord(c) for c in t) - sum(ord(c) for c in s))
# 利用 Counter (标准库的 collections)
# return list(Counter(t) - Counter(s))[0]
方法三:位运算
class Solution:
def findTheDifference(self, s: str, t: str) -> str:
res = 0
for c in s + t:
res ^= ord(c)
return chr(res)
# return chr(reduce(xor, map(ord, s + t)))
方法四:列表排序
class Solution:
def findTheDifference(self, s: str, t: str) -> str:
s = list(s)
t = list(t)
s.sort()
t.sort()
for i in range(len(s)):
if s[i] != t[i]:
return t[i]
return t[-1]
397. 整数替换
方法一:记忆化搜索
class Solution:
@cache # 记忆化搜索
def integerReplacement(self, n: int) -> int:
if n == 1: return 0
if n & 1: # 奇数 加减后除以 2 共两次操作
return 2 + min(self.integerReplacement((n - 1) >> 1), self.integerReplacement((n + 1) >> 1))
return 1 + self.integerReplacement(n >> 1)
方法二:贪心
递归枚举中的「最优解」是固定的。
if n <= 3:return n - 1
偶数
奇数 n % 4 余数为 1 或 3,减一或加一
class Solution:
def integerReplacement(self, n: int) -> int:
res = 0
while n != 1:
if n & 1:
n += -1 if n & 2 == 0 or n == 3 else 1
else:
n >>= 1
res += 1
return res
## 递归
# @lru_cache(None)
def x(n):
if n <= 3: return n - 1
if n & 1 == 0: return 1 + x(n >> 1)
if n & 4 == 1:
return 3 + x((n - 1) >> 2)
return 3 + x((n + 1) >> 2)
return x(n)
405. 数字转换为十六进制数
方法一:位运算
题目要求将给定的整数 num 转换为十六进制数,负整数使用补码运算方法。
在补码运算中,最高位表示符号位,符号位是 0 表示正整数和零,符号位是 1 表示负整数。32 位有符号整数的二进制数有 32 位,由于一位十六进制数对应四位二进制数,因此 32 位有符号整数的十六进制数有 8 位。将 num 的二进制数按照四位一组分成 8 组,依次将每一组转换为对应的十六进制数,即可得到 num 的十六进制数。
假设二进制数的 8 组从低位到高位依次是第 0 组到第 7 组,则对于第 i 组,可以通过 (num >> (4×i)) & 0xf 得到该组的值,其取值范围是 0 到 15(即十六进制的 f)。将每一组的值转换为十六进制数的做法如下:
对于 0 到 9,数字本身就是十六进制数;对于 10 到 15,将其转换为 a 到 f 中的对应字母。
对于负整数,由于最高位一定不是 0,因此不会出现前导零。对于零和正整数,可能出现前导零。避免前导零的做法如下:
如果 num = 0,则直接返回 0;
如果 num > 0,则在遍历每一组的值时,从第一个不是 0 的值开始拼接成十六进制数。
计算机存储 32 位有符号整数。int 型整数存储范围在 [ − 2 31 , 2 31 − 1 ] [-2^{31}, 2^{31} - 1] [−231,231−1] 内,且在计算机内部以补码形式表示,共 32 位,最高位为符号位,负数符号位为 1,正数为 0。
在计算机中, [ 0 , 2 31 − 1 ] [0, 2^{31} - 1] [0,231−1] 范围内的数对应的十六进制存储方式为 0x00000000-0x7FFFFFFF,(0 - 2147483647), [ − 2 31 , − 1 ] [-2^{31},-1] [−231,−1] 范围内的数对应的十六进制存储方式为 0x80000000-0xFFFFFFFF$。(2147483648 - 4294967295)
可以先将负数统一加上 2 32 2^{32} 232,使其映射到 [ 2 31 , 2 32 − 1 ] [2^{31}, 2^{32} - 1] [231,232−1] 范围内,就可以直接进行十六进制转换了。
负数加上 232 其实就是负数的绝对值取补数 232 - abs(num)
也可以通过与运算 &,或模运算 %,统一正负数。
num & 0xffffffff # 余数 num % (2 ** 32 )
print(0xffffffff,2 ** 32 - 1) # 4294967295 4294967295
num & 0xffffffff 这步操作将负数转换为正数,而这个正数的二进制编码正好和 32 位的负数的二进制编码一样,但是对其进行操作却没有对负数的二进制操作那么多限制。
为了方便起见,我们提前将十六进制对应的 16 种不同字符存到字符串 s 中,方便进制转换过程中直接提取。
输入为 0 时,直接返回 “0” ;
输入为正数时,通过不断求余数,最后翻转字符串得到十六进制表示;
输入为负数时,利用补码运算的方法,计算其补码运算后的数字,按正数步骤处理,最后处理符号位,注意,输入负数最小值时,补码运算后为 0 ,与输入为 0 要区分,特殊处理。
class Solution:
def toHex(self, num: int) -> str:
lib, ret = "0123456789abcdef", ""
# 加上 2**32 负数取补数 2**32 - abs(num)
# 1 << 32 = 2 ** 32 = -1 & 0xffffffff + 1 = 4294967296
# n = num + (1 << 32) if num < 0 else num
n = num & 0xffffffff # 余数 num % (2 ** 32 - 1)
if n == 0: return "0"
while n:
# ret = lib[n % 16] + ret
# n //= 16
ret = lib[n & 0xf] + ret # 掩码 0X0000000F -> 15
n >>= 4
return ret
458. 可怜的小猪
特别经典的一道题,1024个桶里,有一个有毒,十个小白鼠可以做测试,怎么一次找到有毒的那个?
将 0~1023 写成二进制,最多是十位,每个小白鼠喝所有某一位为 1 的(一鼠一位)
最终要找的那个就是所有死的小白鼠的位为 1,其他位为 0
十只小白鼠一次可以试出 2^10 个桶,如果是两次呢?
其实两次可以看成三进制,每个小白鼠可以在两轮内试出某一位是 0 还是 1 还是 2
第一次死就是那一位为 1,第二次是那一次为 2,没死就是那一位为 0
这样来看的话,x 轮就该转换成(x + 1)进制, 要找 buckets 在 x + 1 进制下是几位,就是我们至少需要的小白鼠个数了。
class Solution:
def poorPigs(self, buckets: int, minutesToDie: int, minutesToTest: int) -> int:
return ceil(log(buckets, minutesToTest//minutesToDie + 1))
476. 数字的补数
方法一:位运算
找二进制 num 中最高位是 1 的位数 i,然后遍历 num 的第 0 ∼ i 0∼i 0∼i 个二进制位,将它们依次进行取反。可以构造掩码 m a s k = 2 i + 1 − 1 mask = 2^{i+1} - 1 mask=2i+1−1,将 num 与 mask 进行异或运算。
class Solution:
def findComplement(self, num: int) -> int:
for i in range(1, 30 + 1):
if num < (1 << i): break
else: i = 31
# i - 1 是 num 二进制位中最高位是 1 的位数
mask = (1 << i) - 1
return num ^ mask
那怎么获取得与 num 二进制同样长度的 1 呢?
- 按位找最前边的 1;
- 利用 -1 的补码就是全1的(~0 也可以)。然后根据 mask 与 num 相与,判断 mask 的右移是否到位,如果有重合,那一定相与结果会不等于零!
class Solution {
public int findComplement(int num) {
mask = -1 # 0xFFFFFFFF 即全为 1 补码
while (mask & num) > 0:
mask <<= 1
return ~mask ^ num
剑指 Offer II 003. 前 n 个数字二进制中 1 的个数
class Solution {
public int[] countBits(int n) {
int[] ans = new int[n + 1];
int highBit = 0;
for(int i = 1; i < n + 1; i++) {
// ans[i] = Integer.bitCount(i);
// ans[i] = bit1(i);
// ans[i] = bit2(i);
ans[i] = ans[i & (i - 1)] + 1;
// ans[i] = ans[i >> 1] + (i & 1); // 最低位 1,右移分奇偶。
// 记录 i 的最高 bit 位。最高位 1
// if ((i & (i - 1)) == 0) highBit = i;
// ans[i] = ans[i - highBit] + 1;
}
return ans;
}
int bit1(int x){
int res = 0;
while(x > 0){
res += x % 2; x /= 2;
}
return res;
}
int bit2(int x){
int res = 0;
while(x > 0){
x &= x - 1; res++;
}
return res;
}
}
89. 格雷编码
class Solution {
public List<Integer> grayCode(int n) {
List<Integer> res = new ArrayList<>();
for(int i = 0; i < 1 << n; ++i)
res.add(i ^ i >> 1);
return res;
}
}
10、 338. 比特位计数
11、 342. 4的幂
12、371. 两整数之和
17、 461. 汉明距离
18、 476. 数字的补数
19、 477. 汉明距离总和
20、 526. 优美的排列
21、 1178. 猜字谜
22、 1711. 大餐计数
23、 剑指 Offer 15. 二进制中1的个数
边栏推荐
- JS triangle
- 7-18 simple simulation of banking business queue
- Talk about DART's null safety feature
- 消息队列与快递柜之间妙不可言的关系
- 行测-图形推理-2-黑白格类
- 数字藏品加速出圈,MarsNFT助力多元化文旅经济!
- Develop those things: go plus c.free to free memory, and what are the reasons for compilation errors?
- Database daily question --- day 22: last login
- Statistical method for anomaly detection
- Classification and prediction of heartbeat signal
猜你喜欢
微信论坛交流小程序系统毕业设计毕设(5)任务书

How to operate DTC community?

Microbial Health Network, How to restore Microbial Communities
Ligne - raisonnement graphique - 4 - classe de lettres
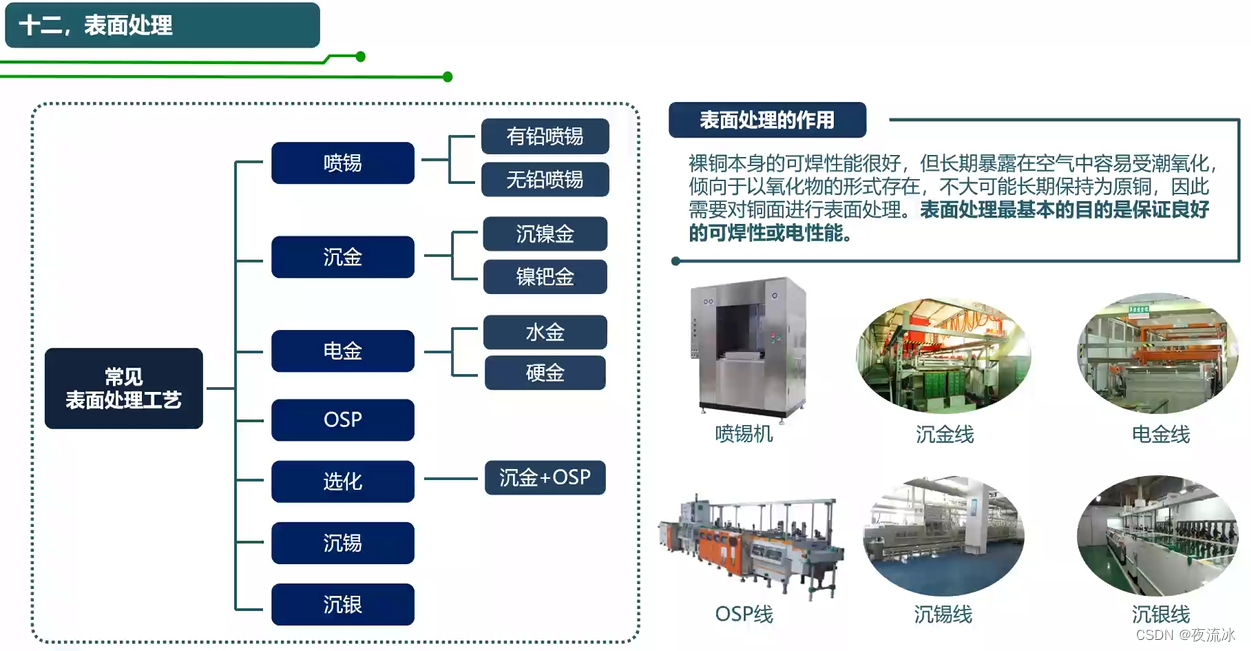
知识点滴 - PCB制造工艺流程
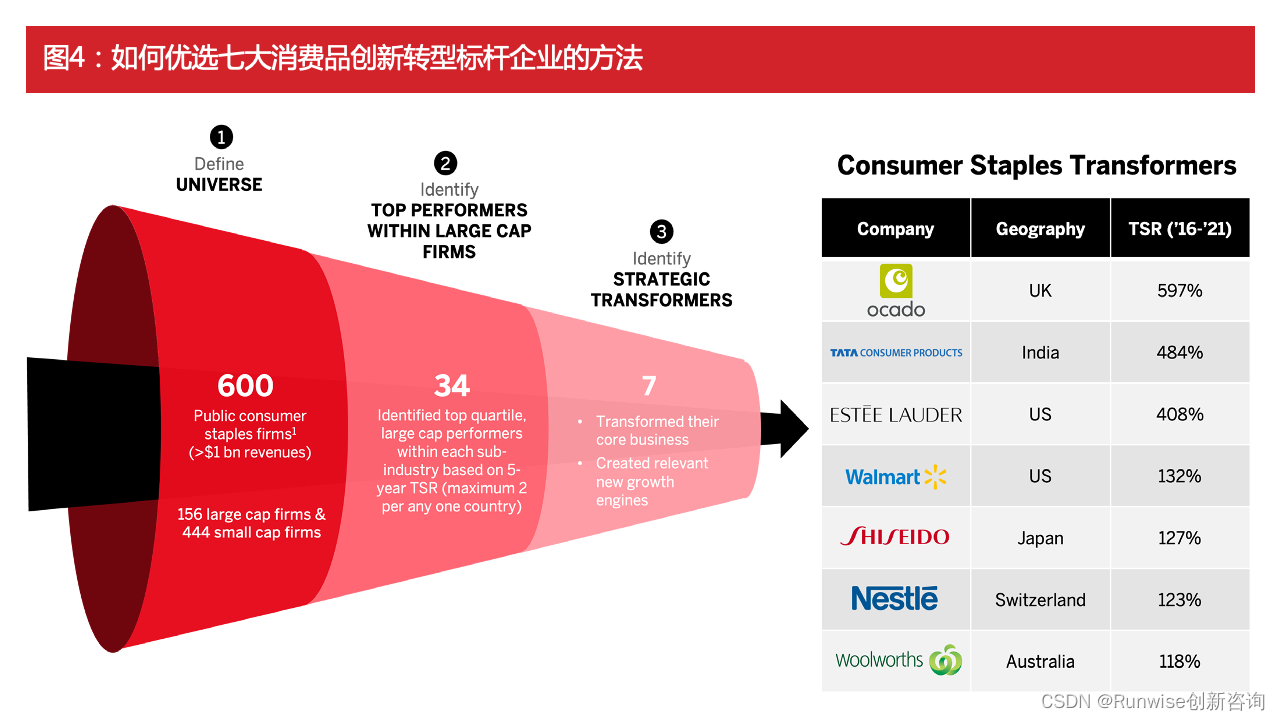
消费品企业敏捷创新转型案例

Brush question 4

30讲 线性代数 第五讲 特征值与特征向量

Online interview, how to better express yourself? In this way, the passing rate will be increased by 50%~
Visual studio 2019 installation
随机推荐
Brush question 4
[network] Introduction to C language
OC variable parameter transfer
Take full control! Create a "leading cockpit" for smart city construction
Anta DTC | Anta transformation, building a growth flywheel that is not only FILA
Sword finger offer 27 Image of binary tree
Cascade-LSTM: A Tree-Structured Neural Classifier for Detecting Misinformation Cascades-KDD2020
About idea cannot find or load the main class
Knowledge drop - PCB manufacturing process flow
Use JfreeChart to generate curves, histograms, pie charts, and distribution charts and display them to jsp-2
QT graphicsview graphical view usage summary with flow chart development case prototype
The wonderful relationship between message queue and express cabinet
今日创见|企业促进创新的5大关键要素
Circumvention Technology: Registry
Line test - graphic reasoning -7- different graphic classes
Two minutes, talk about some wrong understandings of MySQL index
微信论坛交流小程序系统毕业设计毕设(3)后台功能
Leetcode interview question 02.07 Linked list intersection [double pointer]
How to operate DTC community?
行测-图形推理-7-相异图形类