当前位置:网站首页>【统计学习方法】学习笔记——提升方法
【统计学习方法】学习笔记——提升方法
2022-07-07 10:28:00 【镰刀韭菜】
统计学习方法学习笔记——提升方法
提升方法(boosting)是一种常用的统计学习方法,应用广泛且有效。在分类问题中,它通过改变训练样本的权重,学习多个分类器,并将这些分类器进行线性组合,提高分类的性能。 (1)介绍boosting方法的思路和代表性的boosting算法AdaBoost
(2)通过训练误差分析探讨AdaBoost为什么能提高学习精度
(3)从前向分布加法模型的角度解释AdaBoost
(4)最后叙述boosting方法更具体的实例——boosting tree(提升树)
1. 提升方法AdaBoost算法
boosting基本思路:**boosting基于这样一种思想:对于一个复杂任务来说,将多个专家的判断进行适当的综合所得出的判断,要比其中任何一个专家单独的判断好。**实际上就是“三个臭皮匠,顶个诸葛亮”的道理。
强可学习:在概率近似正确(probably approximately correct,PAC)学习的框架中,一个概念,如果存在一个多项式的学习算法能够学习它,并且正确率很高,那么称这个概念是强可学习的。
弱可学习:一个概念,如果存在一个多项式的学习算法能够学习它,学习的正确率仅比随机猜测略好,那么称为弱可学习的。
强可学习和弱可学习:Schapire证明了强可学习与弱可学习是等价的,也就是说,在PAC学习的框架下,一个概念是强可学习的充要条件是这个概念是弱可学习的。
从弱学习到强学习:可将“弱学习”提升为“强学习”,弱学习算法通常比强学习算法容易得多。具体如何实施提升,便称为开发提升方法时要解决的问题。有很多提升算法被提出,最具代表性的就是AdaBoost。
**提升方法就是从弱学习算法出发,反复学习,得到一系列弱分类器(又称为基分类器),然后组合这些弱分类器,构成一个强分类器。**大多数的提升方法都是改变训练数据的概率分布(训练数据的权重分布),针对不同的训练数据分布,调用弱学习算法学习一系列弱分类器。这里就有两个问题。
(1)在每一轮如何改变训练数据的权值或概率分布
(2)如何将弱分类器组合成一个强分类器
对于前面提到的两个问题,AdaBoost的做法是
(1)提高那些被前一轮弱分类器错误分类样本的权重,降低那些被正确分类样本的权重。这样一来,那些没有得到正确分类的数据,由于权值的加大而受到后一轮的弱分类器的更大关注。
(2)加权多数表决,加大分类器误差小的弱分类器的权值,使其在表决中起较大的作用,减小分类误差大的弱分类器的权值,使其在表决中起较小的作用。
算法:AdaBoost
输入:训练数据集 T = ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x N , y N ) T=(x_1,y_1),(x_2,y_2),...,(x_N,y_N) T=(x1,y1),(x2,y2),...,(xN,yN),其中 x i ∈ X ⊆ R n , y i ∈ { − 1 , + 1 } x_i∈\mathcal{X}⊆R^n,y_i\in \{−1,+1\} xi∈X⊆Rn,yi∈{ −1,+1}。弱学习算法。
输出:最终分类器 G ( x ) G(x) G(x)
(1)初始化训练数据的权值分布
D 1 = ( w 11 , . . . , w 1 i , . . . , w 1 N ) , w 1 i = 1 N , i = 1 , 2 , . . . , N D_1=(w_{11},...,w_{1i},...,w_{1N}), w_{1i}=\frac{1}{N}, i=1,2,...,N D1=(w11,...,w1i,...,w1N),w1i=N1,i=1,2,...,N
这里假设了数据具有均匀的权值分布,每个样本在基分类器的学习作用相同。
(2)对m=1,2,…,M
(a)用权值分布为 D m D_m Dm的训练数据学习,得到基分类器 G m ( x ) : X → { + 1 , − 1 } G_m(x):\mathcal{X}→\{+1,−1\} Gm(x):X→{ +1,−1}
(b)计算 G m ( x ) G_m(x) Gm(x)在训练集上的分类误差率
e m = ∑ i = 1 N P ( G m ( x i ) ≠ y i ) = ∑ i = 1 N w m i I ( G m ( x i ) ≠ y i ) = ∑ G m ( x i ) ≠ y i w m i e_m=\sum_{i=1}^N P(G_m(x_i)≠y_i)=\sum_{i=1}^N w_{mi} I(G_{m}(x_i)\ne y_i)=\sum_{G_m(x_i)\ne y_i}w_{mi} em=i=1∑NP(Gm(xi)=yi)=i=1∑NwmiI(Gm(xi)=yi)=Gm(xi)=yi∑wmi
这里, w m i w_{mi} wmi表示第m轮中第i个实例的权值, ∑ i = 1 N w m i = 1 \sum_{i=1}^N w_{mi}=1 ∑i=1Nwmi=1,表明 G m ( x ) G_m(x) Gm(x)在加权的训练数据集上的分类误差率是被 G m ( x ) G_m(x) Gm(x)误分类样本的权值之和。
(c)计算 G m ( x ) G_m(x) Gm(x)的系数: α m = 1 2 log 1 − e m e m α_m=\frac{1}{2} \log{\frac{1−e_m}{e_m}} αm=21logem1−em,对数为自然对数。 α m α_m αm表示 G m ( x ) G_m(x) Gm(x)在最终分类器中的重要性。 e m ⩽ 0.5 e_m⩽0.5 em⩽0.5时 α m ⩾ 0 α_m⩾0 αm⩾0,而且 α m α_m αm随着 e m e_m em的减小而增大,分类误差越小的基分类器在最终分类器中的作用越大。
(d)更新训练集的权值分布,为下一轮做准备
D m + 1 = ( w m + 1 , 1 , . . . , w m + 1 , i , . . . , w m + 1 , N ) D_{m+1}=(w_{m+1,1},...,w_{m+1,i},...,w_{m+1,N}) Dm+1=(wm+1,1,...,wm+1,i,...,wm+1,N)
w m 1 , i = { w m i z m e − α m , G m ( x i ) = y i w m i z m e α m , G m ( x i ) ≠ y i w_{m_1, i}=\left\{\begin{matrix} \frac{w_{mi}}{z_m}e^{-\alpha _m}, & G_{m}(x_i)=y_i \\ \frac{w_{mi}}{z_m}e^{\alpha _m}, & G_{m}(x_i)\ne y_i \end{matrix}\right. wm1,i={ zmwmie−αm,zmwmieαm,Gm(xi)=yiGm(xi)=yi
Z m = ∑ i = 1 N w m i e x p ( − α m y i G m ( x i ) ) Z_m=\sum_{i=1}^N w_{mi}exp(−α_my_iG_m(x_i)) Zm=i=1∑Nwmiexp(−αmyiGm(xi))
其中 Z m Z_m Zm为规范化因子。
误分类样本权值变大,正确分类样本权值缩小,两相比较放大了 e 2 α m = 1 − e m e m e^{2\alpha_m}=\frac{1−e_m}{e_m} e2αm=em1−em倍。
(3)构建基分类器的线性组合
f ( x ) = ∑ m = 1 M α m G m ( x ) f(x)=\sum_{m=1}^M α_mG_m(x) f(x)=m=1∑MαmGm(x)
最终分类器为
G ( x ) = s i g n ( f ( x ) ) G(x)=sign(f(x)) G(x)=sign(f(x))
注意 α m α_m αm之和不为1。
2. AdaBoost算法的训练误差分析
AdaBoost最基本的性质是它能在学习过程中不断减少训练误差。
定理8.1(AdaBoost的训练误差界):AdaBoost算法最终分类器的训练误差界为
1 N ∑ i = 1 N I ( G ( x i ) ≠ y i ) ⩽ 1 N ∑ i e x p ( − y i f ( x i ) ) = ∏ m Z m \frac{1}{N}\sum_{i=1}^{N} I(G(x_i)≠y_i)⩽\frac{1}{N}\sum_i exp(−y_if(x_i))=\prod_m Z_m N1i=1∑NI(G(xi)=yi)⩽N1i∑exp(−yif(xi))=m∏Zm
定理8.2 (二分类问题AdaBoost的训练误差界)
∏ m = 1 M Z m = ∏ m = 1 M [ 2 e m ( 1 − e m ) ] = ∏ m = 1 M 1 − 4 γ m 2 ≤ e x p ( − 2 ∑ m = 1 M γ m 2 ) \prod_{m=1}^M Z_m=\prod_{m=1}^{M} [2\sqrt{e_m(1−e_m)}]=\prod_{m=1}^{M}\sqrt{1−4\gamma_m^2} \le exp(−2\sum_{m=1}^{M}\gamma_m^2) m=1∏MZm=m=1∏M[2em(1−em)]=m=1∏M1−4γm2≤exp(−2m=1∑Mγm2)
这里 γ m = 1 2 − e m \gamma_m=\frac{1}{2}−e_m γm=21−em。
推论8.1:如果存在 γ > 0 \gamma>0 γ>0,对所有m有 γ m ⩾ γ \gamma_m⩾\gamma γm⩾γ,则
1 N ∑ i = 1 N I ( G ( x i ) ≠ y i ) ⩽ e x p ( − 2 M γ 2 ) \frac{1}{N}\sum_{i=1}^{N} I(G(x_i)≠y_i)⩽exp(−2M\gamma^2) N1i=1∑NI(G(xi)=yi)⩽exp(−2Mγ2)
这表明在此条件下AdaBoost的训练误差是以指数速率下降的,这一性质当然很有吸引力。
与一些早期的提升方法不同,AdaBoost具有适应性,即它能适应弱分类器各自的训练误差率。这也是它名称的由来,Ada是Adaptive的简写。
3. AdaBoost算法的解释
可以认为AdaBoost算法是模型为加法模型、损失模型为指数模型、学习算法为前向分布算法时的二类分类学习方法。
3.1 前向分布算法
考虑加法模型(additive model)
f ( x ) = ∑ m = 1 M β m b ( x ; γ m ) f(x)=\sum_{m=1}^M β_m b(x; γ_m) f(x)=m=1∑Mβmb(x;γm)
其中, b ( x ; γ m ) b(x; \gamma_m) b(x;γm)为基函数, γ m \gamma_m γm为基函数的参数, β m \beta_m βm为基函数的系数。
在给定训练集和损失函数 L ( y , f ( x ) ) L(y,f(x)) L(y,f(x))的条件下,学习加法模型 f ( x ) f(x) f(x)成为经验风险极小化即损失函数极小化问题:
min β m , γ m ∑ i = 1 N L ( y i , ∑ m = 1 M β m b ( x i ; γ m ) ) \min_{β_m,γ_m}\sum_{i=1}^N L(y_i,\sum_{m=1}M β_mb(x_i; γ_m)) βm,γmmini=1∑NL(yi,m=1∑Mβmb(xi;γm))
通常这是一个复杂的优化问题。前向分步算法求解这一优化问题的想法是:从前向后,每一步只学习一个基函数及其系数,逐步逼近优化目标函数式,那么就可以简化优化的复杂度。每步优化如下损失:
min β , γ ∑ i = 1 N L ( y i , β b ( x i ; γ ) ) \min_{β,γ}\sum_{i=1}^N L(y_i,βb(x_i; γ)) β,γmini=1∑NL(yi,βb(xi;γ))
给定训练数据集 T = ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x N , y N ) T=(x_1,y_1),(x_2,y_2),...,(x_N,y_N) T=(x1,y1),(x2,y2),...,(xN,yN),其中 x i ∈ X ⊆ R n , y i ∈ { − 1 , + 1 } x_i∈\mathcal{X}⊆R^n,y_i\in \{−1,+1\} xi∈X⊆Rn,yi∈{ −1,+1}。损失函数 L ( y , f ( x ) ) L(y,f(x)) L(y,f(x))和基函数的集合 { b ( x ; γ ) } \{b(x; \gamma)\} { b(x;γ)},学习加法模型 f ( x ) f(x) f(x)的前向步骤算法如下:
这样,前向分步算法将同时求解从 m = 1 m=1 m=1到 M 所有参数 β m \beta_m βm , γ m \gamma_m γm的优化问题简化为逐次求解各个 β m \beta_m βm , γ m \gamma_m γm的优化问题。
3.2 前向分布算法与AdaBoost
由前向分步算法可以推导出AdaBoost,用定理叙述这一关系。
定理8.3:AdaBoost算法是前向分步加法算法的特例。这时,模型是由基本分类器组成的加法模型,损失函数是指数函数。
4. 提升树
提升树是以分类树或回归树为基本分类器的提升方法。提升树被认为是统计学习中性能最好的方法之一。
4.1 提升树模型
提升方法实际采用加法模型(即基函数的线性组合)与前向分步算法。以决策树为基函数的提升方法称为提升树(boosting tree)。对分类问题决策树是二叉分类树,对回归问题决策树是二叉回归树。
提升树模型可以表示为决策树的加法模型:
f M ( x ) = ∑ m = 1 M T ( x ; θ m ) f_M(x)=\sum_{m=1}^M T(x; θ_m) fM(x)=m=1∑MT(x;θm)
其中, T ( x ; θ m ) T(x;θ_m) T(x;θm)表示决策树, θ m θ_m θm为决策树的参数, M M M为树的个数。
4.2 提升树算法
提升树算法采用前向分步算法。首先确定初始提升树 f 0 ( x ) = 0 f_0(x)=0 f0(x)=0,第m步的模型是
f m ( x ) = f m − 1 ( x ) + T ( x ; θ m ) f_m(x)=f_{m-1}(x)+T(x;\theta_m) fm(x)=fm−1(x)+T(x;θm)
其中, f m − 1 ( x ) f_{m-1}(x) fm−1(x)为当前模型,通过经验风险极小化确定下一棵决策树的参数 θ m θ_m θm。
θ ^ m = a r g min θ m ∑ i = 1 N L ( y i , f m − 1 ( x i ) + T ( x i ; θ m ) ) \hat{\theta}_m=arg\min_{θ_m}\sum_{i=1}{N} L(y_i,f_{m−1}(x_i)+T(x_i;θ_m)) θ^m=argθmmini=1∑NL(yi,fm−1(xi)+T(xi;θm))
由于树的线性组合可以很好地拟合训练数据,即使数据中的输入与输出之间的关系很复杂。所以提升树是一个高功能的学习算法。
提升树的学习算法:下面讨论对不同问题的提升树学习算法,其主要区别在于使用的损失函数不同。包括用指数损失的分类问题,用平方损失的回归问题,以及用一般损失的一般决策问题。
对于二分类问题,只需将AdaBoost的基分类器限制为二分类树即可,可以说这时的提升树算法是Adaboost算法的特例。
回归问题的提升树,将输入空间X划分为J个互不相交的区域 R 1 , R 2 , . . . , R J R_1,R_2,...,R_J R1,R2,...,RJ,并且在每个区域上确定输出的常量 c j c_j cj,那么树可以表示为
T ( x i ; θ ) = ∑ j = 1 J c j I ( x ∈ R j ) T(x_i;θ)=\sum_{j=1}^J c_j I(x\in R_j) T(xi;θ)=j=1∑JcjI(x∈Rj)
其中,参数 θ = { ( R 1 , c 1 ) , ( R 2 , c 2 ) , . . . , ( R J , c J ) } θ=\{(R_1,c_1),(R_2,c_2),...,(R_J,c_J)\} θ={ (R1,c1),(R2,c2),...,(RJ,cJ)}表示树的区域划分和各区域上的常数。 J J J是回归树的复杂度即叶结点个数。
回归问题提升树使用以下前向分步算法:
f 0 ( x ) = 0 f m ( x ) = f m − 1 ( x ) + T ( x ; θ m ) , m = 1 , 2 , . . . , M f M ( x ) = ∑ i = 1 M T ( x ; θ m ) f_0(x)=0 \\\\ f_m(x) = f_{m−1}(x)+T(x;θ_m), m=1,2,...,M \\\\ f_M(x)=\sum_{i=1}^{M} T(x;θ_m) f0(x)=0fm(x)=fm−1(x)+T(x;θm),m=1,2,...,MfM(x)=i=1∑MT(x;θm)
在前向分步算法的第m步,给定当前模型 f m − 1 ( x ) f_{m−1}(x) fm−1(x),需求解
θ ^ m = a r g min θ m ∑ i = 1 N L ( y i , f m − 1 ( x i ) + T ( x i ; θ m ) ) \hat{\theta}_m=arg\min_{θ_m}\sum_{i=1}^{N} L(y_i,f_{m−1}(x_i)+T(x_i;θ_m)) θ^m=argθmmini=1∑NL(yi,fm−1(xi)+T(xi;θm))
得到 θ ^ m \hat{\theta}_m θ^m,即第m棵树的参数。
当采用平方损失时, L ( y , f ( x ) ) = ( y − f ( x ) ) 2 L(y, f(x))=(y-f(x))^2 L(y,f(x))=(y−f(x))2,其损失变成
L ( y , f m − 1 ( x ) + T ( x ; θ m ) ) = [ y − f m − 1 ( x ) − T ( x ; θ m ) ] 2 = [ r − T ( x ; θ m ) ] 2 L(y, f_{m−1}(x)+T(x;θ_m))=[y−f_{m−1}(x)−T(x;θ_m)]^2=[r−T(x;θ_m)]^2 L(y,fm−1(x)+T(x;θm))=[y−fm−1(x)−T(x;θm)]2=[r−T(x;θm)]2
这里, r = y − f m − 1 ( x ) r=y−f_{m−1}(x) r=y−fm−1(x),是当前模型拟合数据的残差。所以,对回归问题的提升树算法来说,只需简单地拟合当前模型的残差。
算法:回归问题的提升树算法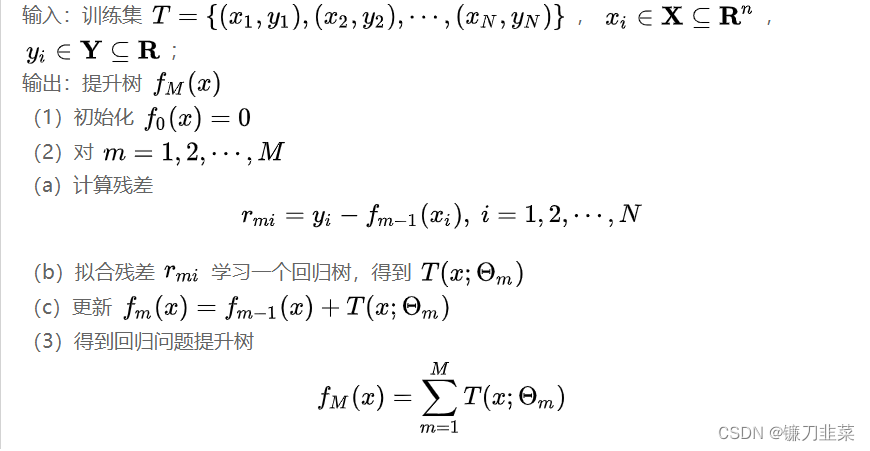
4.3 梯度提升
提升树利用加法模型与前向分步算法实现学习的优化过程,当损失函数是平方损失和指数损失函数时,每一步优化是很简单的,但对一般损失函数而言,往往每一步优化并不那么容易。针对这一问题,Freidman提出了梯度提升(gradient boosting)算法,这是利用最速下降法的近似方法,其关键是利用损失函数的负梯度在当前模型的值 − [ ∂ L ( y , f ( x i ) ) ∂ f ( x i ) ] f ( x ) = f m − 1 ( x ) -[\frac{\partial L(y,f(x_i))}{\partial f(x_i)}]_{f(x)=f_{m-1}(x)} −[∂f(xi)∂L(y,f(xi))]f(x)=fm−1(x)作为回归问题提升树算法中残差的近似值,拟合一个回归树。
算法:梯度提升算法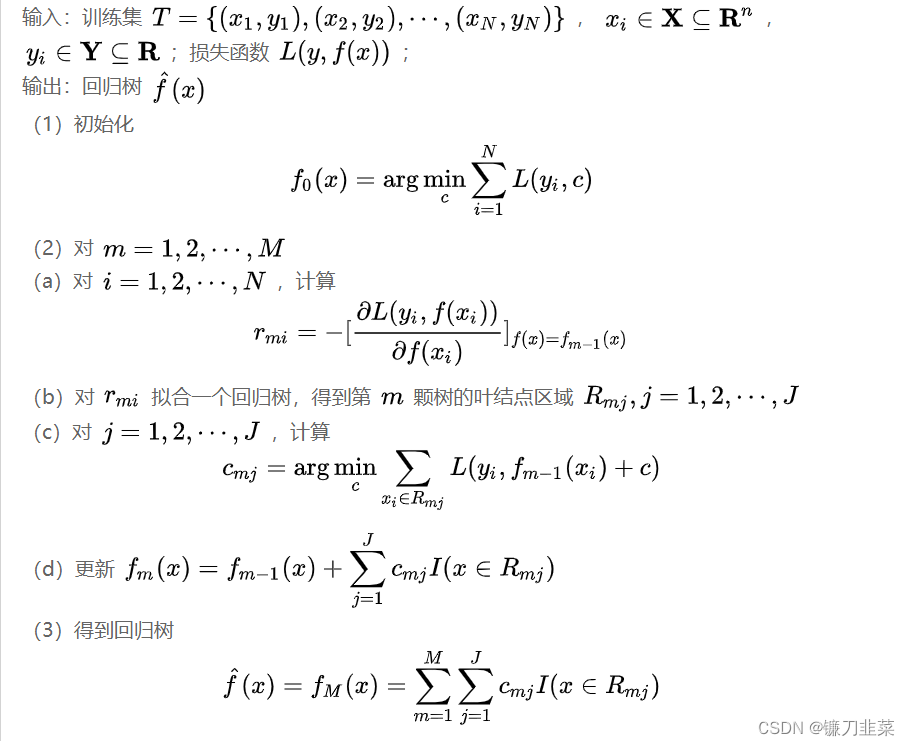
总结
- 提升方法是将弱学习算法提升为强学习算法的统计学习方法。
- AdaBoost模型是弱分类器的线性组合。
- AdaBoost算法的特点是通过迭代每次学习一个基本分类器。
- AdaBoost的每次迭代可以减少它在训练数据集上的分类误差率。
- 提升树是以分类树或者回归树为基本分类器的提升方法。
补充
Gradient Boosting
Gradient Boosting Machine(简称GBM),由Freidman提出,是一类以梯度提升为基本思想的算法。
经典的AdaBoost算法只能处理采用指数损失函数的二分类学习任务(当然,现在已经有能够处理多分类或回归任务的AdaBoost算法变种),而Gradient Boosting通过设置不同的可微损失函数可以处理各类学习任务(分类、回归、排序等),应用范围大大扩展。
AdaBoost对异常点(outlier)比较敏感,而Gradient Boosting通过引入bagging思想、加入正则项等方法能够有效地抵御训练数据中的噪音,具有更好的健壮性。
Gradient Boosting的基本思想是,将负梯度作为上一轮学习犯错的衡量指标,在下一轮学习中通过拟合负梯度来纠正上一轮犯的错误。这里的关键问题是:为什么通过拟合负梯度就能纠正上一轮的错误了?Freidman给出的答案是:函数空间的梯度下降。
GBDT
梯度提升树,常简称为GBDT(Gradient Boosting Decision Tree),或者是GBT(Gradient Boosting Tree),GTB(Gradient Tree Boosting ),GBRT(Gradient Boosting Regression Tree),MART(Multiple Additive Regression Tree)。GBDT在实际业务中得到了广泛应用,在机器学习算法中占有重要的一席之地。GBDT采用的是CART中的回归树
在解决分类问题时,GBDT常用的损失函数有:指数损失(退回到Adaboost)、负对数损失。指数损失容易受异常点影响,且只能用于二分类问题,因此sklearn中GradientBoostingClassifier的默认损失函数选得是后者。
在解决回归问题时,GBDT常用的损失函数有:均方差损失、绝对损失、Huber损失和分位数损失。对于Huber损失和分位数损失,常用于健壮回归,可以减少异常点对损失函数的影响,相反,均方差损失容易受到异常点的影响。
XGBoost
XGBoost是对GBDT的扩展实现,不仅在速度上更加高效,而且在算法推导上也有所改进。二者的主要差别如下:
- GBDT以CART回归树作为基学习器,XGBoost则支持gbtree、dart和gblinear三种基学习器。其中,前二者都是基于树的模型,dart还考虑了dropout思想,gblinear则是线性模型,这个时候XGBoost相当于带L1和L2正则化项的逻辑回归(分类问题)或者线性回归(回归问题)。
- GBDT在优化时只用到一阶导数信息,XGBoost则对代价函数进行了二阶泰勒展开,同时用到了一阶和二阶导数。顺便提一下,XGBoost工具支持自定义代价函数,只要函数一阶和二阶可导。
更本质一点来说,GBDT主要对loss L ( y , F ) L(y,F) L(y,F) 关于 F F F 求梯度,利用回归树拟合该负梯度;XGBoost主要对loss L ( y , F ) L(y,F) L(y,F) 二阶泰勒展开,然后求解析解,以解析解 o b j obj obj作为标准,贪心搜索split树是否 o b j obj obj更优,更直接。 - XGBoost在代价函数里加入了正则项,用于控制模型的复杂度。正则项里包含了树的叶子节点个数、每个叶子节点上输出的score的L2模的平方和。从bias-variance tradeoff角度来讲,正则项降低了模型的variance,使学习出来的模型更加简单,防止过拟合。
- XGBoost借鉴了随机森林的做法,支持列抽样(column subsampling),即随机选取部分特征进行学习,这不仅能降低过拟合,还能减少计算。
- 对于特征的值有缺失的样本,XGBoost可以自动学习出它的分裂方向。
- XGBoost工具支持并行。需要注意的是,这里的并行不是tree粒度的并行,XGBoost也是一次迭代完才能进行下一次迭代的(第t次迭代的代价函数里包含了前面t-1次迭代的预测值),XGBoost的并行是在特征粒度上的。
我们知道,决策树的学习最耗时的一个步骤就是对特征的值进行排序(因为要确定最佳分割点),XGBoost在训练前,预先对数据进行排序,保存为block结构,后面的迭代中重复使用这个结构,大大减小计算量。这个block结构也使得并行成为可能:在进行节点的分裂时,需要计算每个特征的增益,最终选增益最大的那个特征去做分裂,那么各个特征的增益计算就可以开多线程进行,达到并行目的。 - 树节点在进行分裂时,我们需要计算每个特征的每个分割点对应的增益,即用贪心法枚举所有可能的分割点。当数据无法一次载入内存或者在分布式情况下,贪心算法效率就会变得很低,所以XGBoost还提出了一种可并行的近似直方图算法,用于高效地生成候选的分割点。
- XGBoost中的回归树和GBDT所使用的CART回归树并不一致,后者的叶结点输出值,是分到该叶结点的所有样本点的均值,前者的叶结点输出值是根据打分公式计算出来的。
- Boosting主要关注降低bias,因此Boosting能基于泛化性能相当弱的学习器构建出很强的集成;Bagging主要关注降低variance,因此它在不剪枝的决策树、神经网络等学习器上效用更为明显。
LightGBM是微软近年来开源的库,相较于XGBoost,它的速度更快并且内存占用更低。LightGBM的改进点主要在于以下几方面:
- 采用直方图算法寻找分割点,减小内存占用、加速
- 采用Leaf-wise的方式建树,提升准确率
- 对并行学习的优化
- 减少训练集(GOSS)、减少特征(EFB)
内容来源
[1] 《统计学习方法》 李航
[2] https://www.cnblogs.com/liaohuiqiang/p/10980080.html
[3] 《统计学习方法》系列(8)
边栏推荐
- "Series after reading" my God! It's so simple to understand throttling and anti shake~
- [play RT thread] RT thread Studio - key control motor forward and reverse rotation, buzzer
- Fleet tutorial 15 introduction to GridView Basics (tutorial includes source code)
- The function of adding @ before the path in C #
- 2022 8th "certification Cup" China University risk management and control ability challenge
- Problem: the string and characters are typed successively, and the results conflict
- 《通信软件开发与应用》课程结业报告
- About web content security policy directive some test cases specified through meta elements
- How to connect 5V serial port to 3.3V MCU serial port?
- Vxlan 静态集中网关
猜你喜欢

Learning and using vscode

H3C HCl MPLS layer 2 dedicated line experiment
![An error occurred when vscade tried to create a file in the target directory: access denied [resolved]](/img/14/9899f5a765872fb3238be4305a2dc7.png)
An error occurred when vscade tried to create a file in the target directory: access denied [resolved]

2022 年第八届“认证杯”中国高校风险管理与控制能力挑战赛
数据库系统原理与应用教程(011)—— 关系数据库
消息队列消息丢失和消息重复发送的处理策略
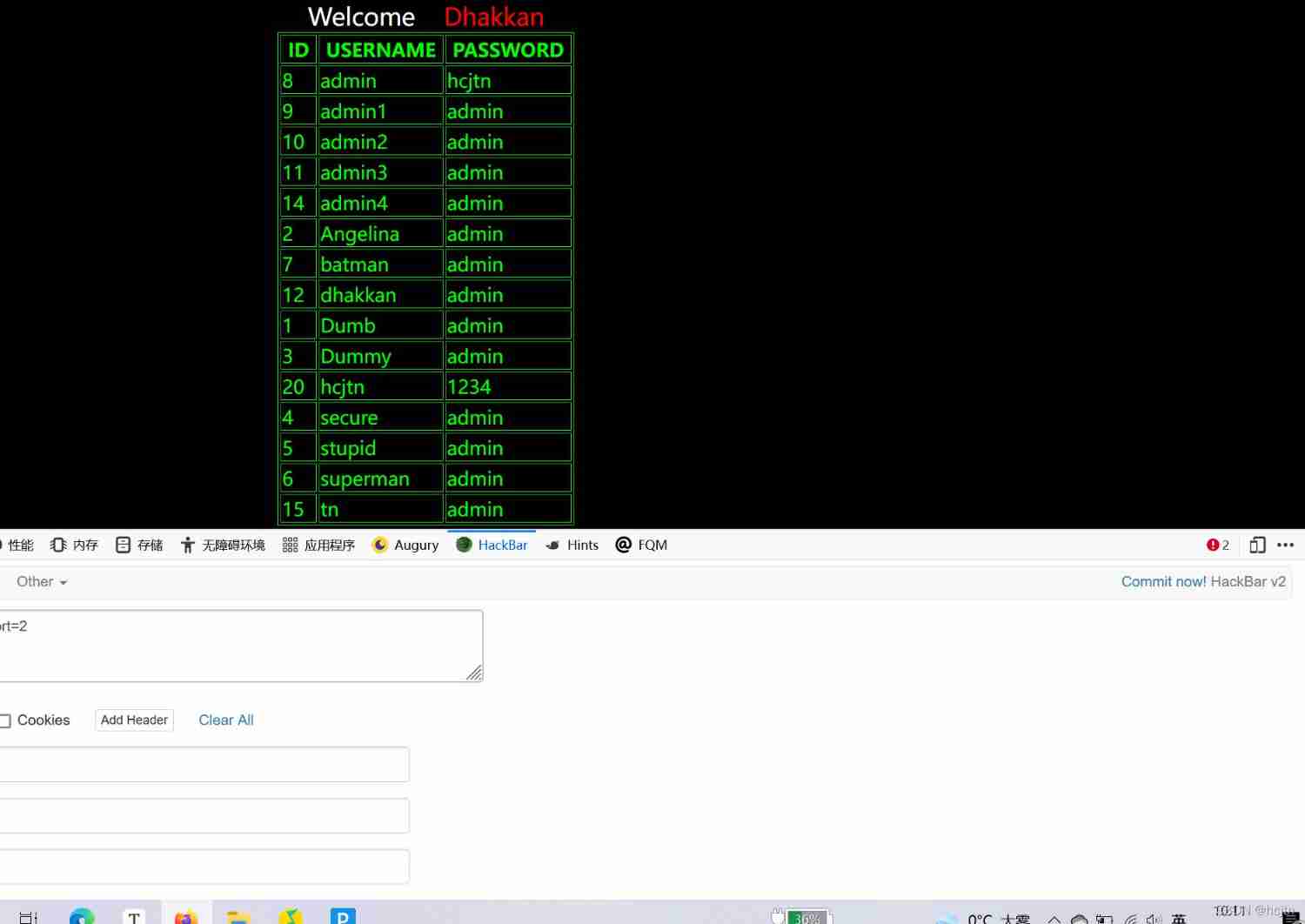
SQL Lab (46~53) (continuous update later) order by injection

Xiaohongshu microservice framework and governance and other cloud native business architecture evolution cases
Hi3516全系统类型烧录教程
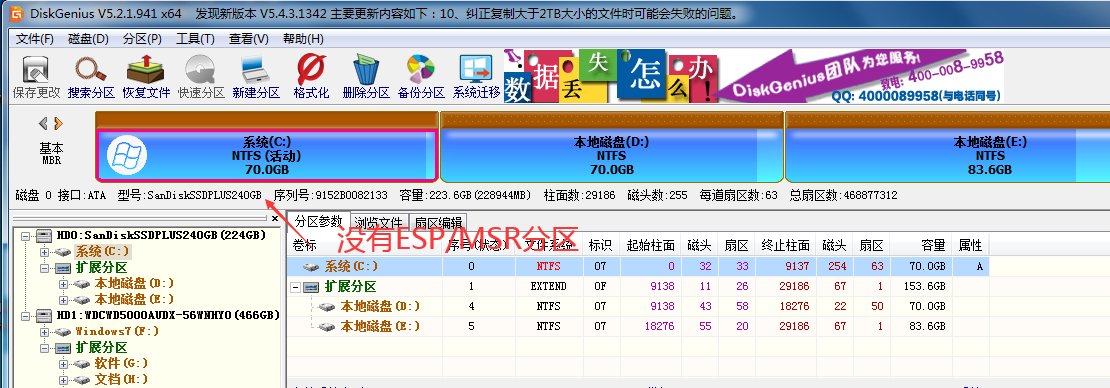
什么是ESP/MSR 分区,如何建立ESP/MSR 分区
随机推荐
VSCode的学习使用
111.网络安全渗透测试—[权限提升篇9]—[Windows 2008 R2内核溢出提权]
SQL Lab (32~35) contains the principle understanding and precautions of wide byte injection (continuously updated later)
SQL Lab (36~40) includes stack injection, MySQL_ real_ escape_ The difference between string and addslashes (continuous update after)
Sonar:cognitive complexity
Problem: the string and characters are typed successively, and the results conflict
Solve server returns invalid timezone Go to ‘Advanced’ tab and set ‘serverTimezone’ property manually
112. Network security penetration test - [privilege promotion article 10] - [Windows 2003 lpk.ddl hijacking rights lifting & MSF local rights lifting]
About sqli lab less-15 using or instead of and parsing
Let digital manage inventory
SQL injection -- Audit of PHP source code (take SQL lab 1~15 as an example) (super detailed)
Flet tutorial 17 basic introduction to card components (tutorial includes source code)
H3C HCl MPLS layer 2 dedicated line experiment
SQL Lab (41~45) (continuous update later)
Present pod information to the container through environment variables
顶级域名有哪些?是如何分类的?
小红书微服务框架及治理等云原生业务架构演进案例
zero-shot, one-shot和few-shot
The left-hand side of an assignment expression may not be an optional property access.ts(2779)
免备案服务器会影响网站排名和权重吗?