当前位置:网站首页>3. C language uses algebraic cofactor to calculate determinant
3. C language uses algebraic cofactor to calculate determinant
2022-07-06 13:26:00 【It's Wang Jiujiu】
Catalog
1. The principle of algebraic cofactor calculating determinant
Second order determinant calculation
Third order determinant calculation
Calculation of determinant Det
3. The shortcomings of this method
1. The principle of algebraic cofactor calculating determinant
Be careful : Determinant must be a square matrix !
Second order determinant calculation
Killing method :
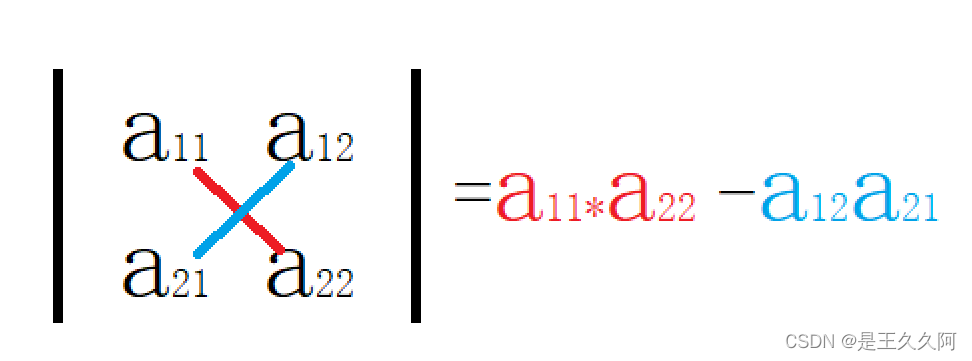
The calculation method of second-order determinant is very simple , Multiply the main diagonal elements — Multiply the sub diagonal elements , So it is also called killing method .
Third order determinant calculation
Scribing method :
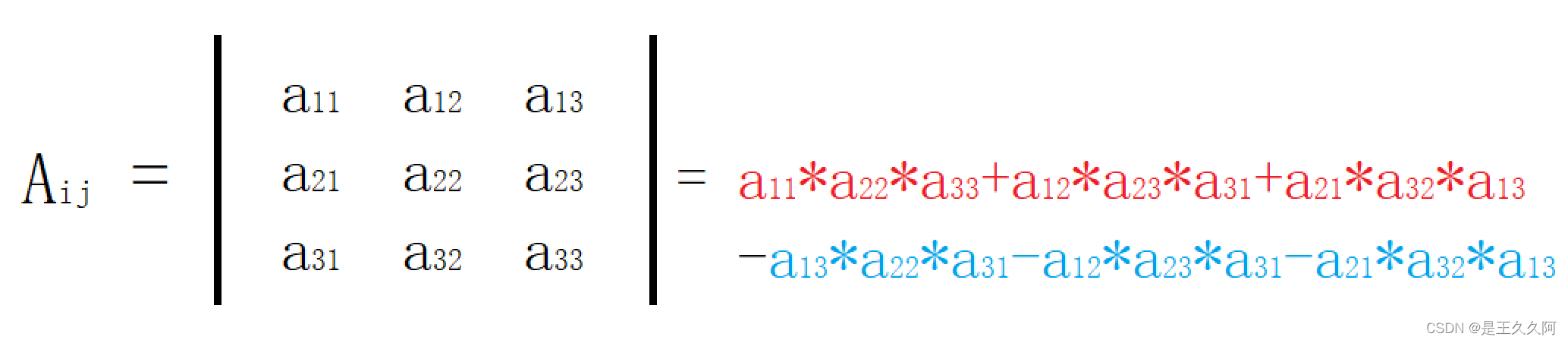
The scribing method is shown in the figure below
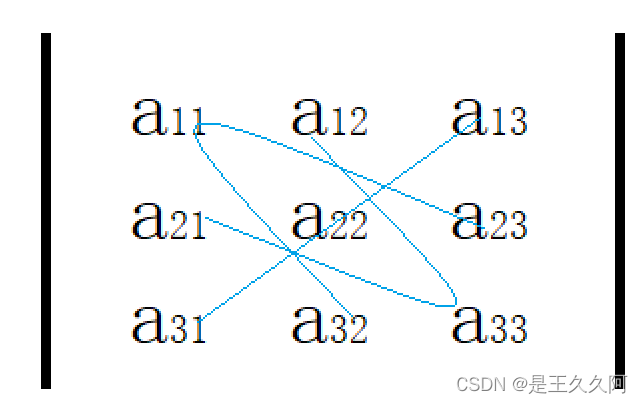
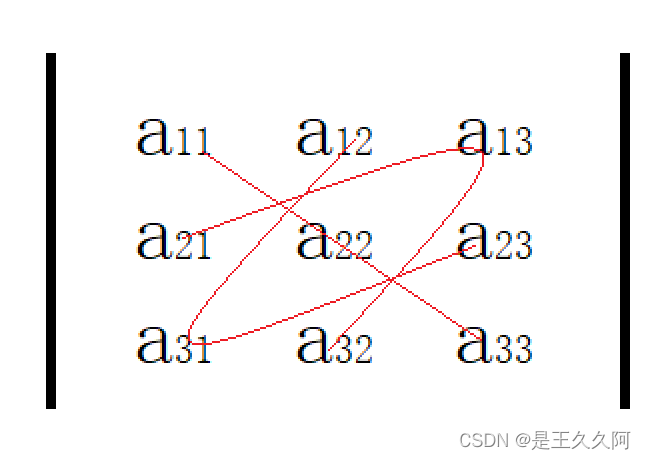
Calculated by definition
When calculating determinant , It can be expanded by row or column for calculation
Take the third-order determinant as an example :

Let's make the determinant A Expand by the first line :
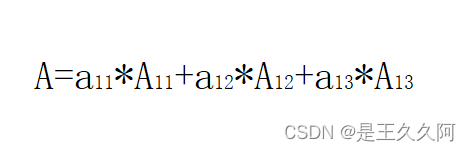
among ,Aij by aij The algebraic covalent of (i Is line number ,j For column number ), for example :A11 by a11 The algebraic covalent of .
Calculation method of algebraic cofactor :
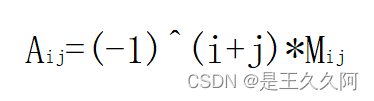
among ,(-1)^(i+j) Expressed as -1 Of i+j Power , Used to determine the positive and negative of algebraic cofactor ,Mij It is remainder formula .
The remainder formula :
Determinant to its i That's ok j Column , The remaining elements form a new determinant , The matrix is aij The Yu Zi form of .
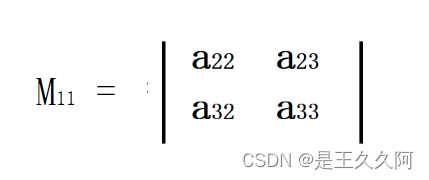
for example ,a11 The remainder of is :
Go to the first row and the first column , The remaining elements are combined into a new determinant according to the existing arrangement .
When calculating the value of determinant , We can choose 0 Expand the extra row and column , Greatly reduce the amount of calculation .
2. Code implementation
The core idea :
When we find the value of higher-order determinant , We can use the method of finding algebraic cofactor to gradually transform the problem of finding high-order determinant into the problem of finding low-order determinant . utilize recursive The idea of can solve such problems , Make big things small , It's trivial .
Input matrix main
stay C In language , A matrix can be stored using a two-dimensional array .
Of course, using arrays to store matrices also has its drawbacks : The size of the array cannot be changed . Before learning dynamic programming , You can open up enough memory space according to the size used , To deal with this problem .
When inputting determinant , We also need to determine its order n To calculate .
#include <stdio.h>
#include <math.h>
#include<assert.h>
#define COL 10// Maximum memory for two-dimensional arrays
int main()
{
int arr[COL][COL] = { 0 };
int i = 0, j = 0;
int n = 0;// Order
printf(" Determinant order :>");
scanf("%d", &n);
printf(" Please enter the determinant :>\n");
for (i = 0; i < n; i++)
{
for (j = 0; j < n; j++)
{
scanf("%d", &arr[i][j]);
}
}
printf("%d", Det(arr, n));
}Calculation of determinant Det
because 1 The determinant of order does not need to be calculated , Is itself , and 3 rank 、2 The determinant of order can be calculated according to the scribing method and the killing method , Here you can set the condition of recursion to n>3, Only determinants of order 4 and above are recursive , The determinant below the fourth order can be calculated directly .
- Before determinant calculation , To ensure the security of the array , When receiving the array, add const, Ensure that the array cannot be modified inside the function .
- The order of determinant is only greater than or equal to 1 Only when makes sense , Use at the beginning of the function assert Assertion n Is it greater than 0: If the condition is true, the function runs , The condition is false assert A warning will be given ,assert Need to include header file .
int Cof(const int arr2[COL][COL], int i, int n);// Statement : Calculate determinant
// Calculate determinant
int Det(const int arr[COL][COL], int n)
{
assert(n > 0);
int sum = 0;
int i = 0;
if (n == 1)//1 The order determinant leads directly to the result
{
sum = arr[0][0];
}
else if (n == 2)
{
sum = arr[0][0] * arr[1][1] - arr[0][1] * arr[1][0];// Kill method to solve
}
else if (n == 3)
{
sum = arr[0][0] * arr[1][1] * arr[2][2]
+ arr[0][1] * arr[1][2] * arr[2][0]
+ arr[1][0] * arr[2][1] * arr[0][2]
- arr[0][2] * arr[1][1] * arr[2][0]
- arr[0][1] * arr[1][0] * arr[2][2]
- arr[1][2] * arr[2][1] * arr[0][0];// Solve by scribing
}
else
{
for (i = 0; i < n; i++)// Expand by the first line
{
if (arr[0][i] != 0)// The expanded item is not 0 Only calculated
{
sum += ((int)pow(-1, i + 2)) * arr[0][i] * (Cof(arr, i, n));//2 Continue recursion above order
}
else
sum += 0;// The expansion item is 0
}
}
return sum;
}The remainder formula Cof
receive Det The two-dimensional array passed by the function , Take its place , The remaining elements form a new two-dimensional array and then pass it to Det function . The two functions call each other , Until the order is less than 4.
int Det(const int arr[COL][COL], int n);// Statement : Computing algebraic cofactor
// Find the remainder formula
int Cof(const int arr[COL][COL], int i, int n)
{
assert(n > 0);
int k = 0;
int j = 0;
int arr2[COL][COL] = { 0 };
for (k = 0; k < n - 1; k++)// Remove 0 That's ok i Column , The rest forms a new matrix
{
for (j = 0; j < n - 1; j++)
{
if (j < i)
{
arr2[k][j] = arr[k + 1][j];
}
else
{
arr2[k][j] = arr[k + 1][j + 1];
}
}
}
return Det(arr2, n - 1);
}3. The shortcomings of this method
Although we have set up many methods to avoid useless recursion
- The expansion item is 0 Then the calculation is not carried out
- 3 Direct calculation of determinant below order
But it is still insufficient to find the determinant of higher order : If you ask 10 Step determinant , Recursion is required 10!/ 6=604,800 Time , Deep recursion eventually causes the program to run very slowly .
边栏推荐
- Iterable、Collection、List 的常见方法签名以及含义
- View UI plus released version 1.2.0 and added image, skeleton and typography components
- 初识C语言(上)
- [中国近代史] 第五章测验
- 10 minutes pour maîtriser complètement la rupture du cache, la pénétration du cache, l'avalanche du cache
- 9.指针(上)
- 初识指针笔记
- 继承和多态(下)
- 2.初识C语言(2)
- View UI plus releases version 1.1.0, supports SSR, supports nuxt, and adds TS declaration files
猜你喜欢
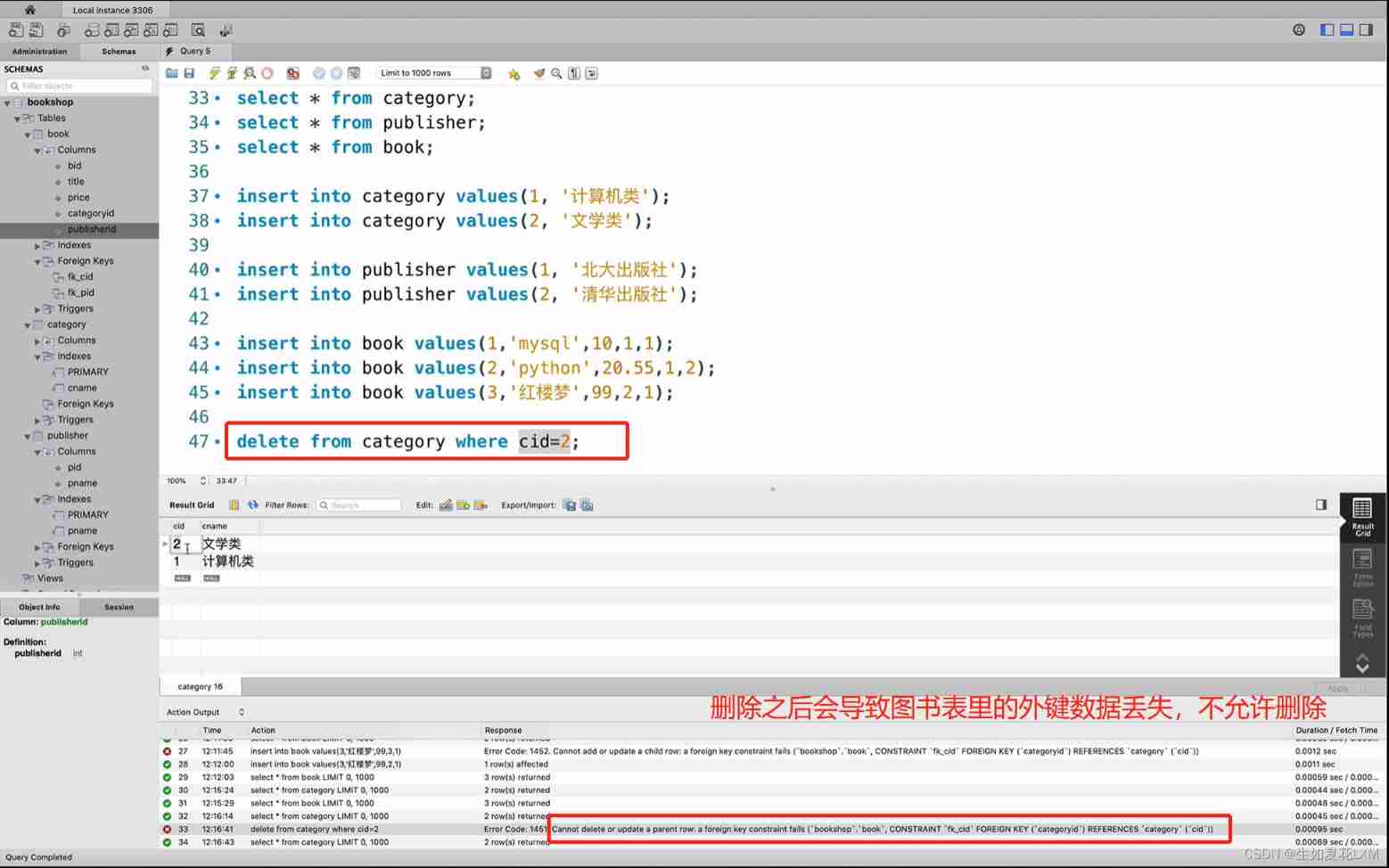
MySQL Database Constraints
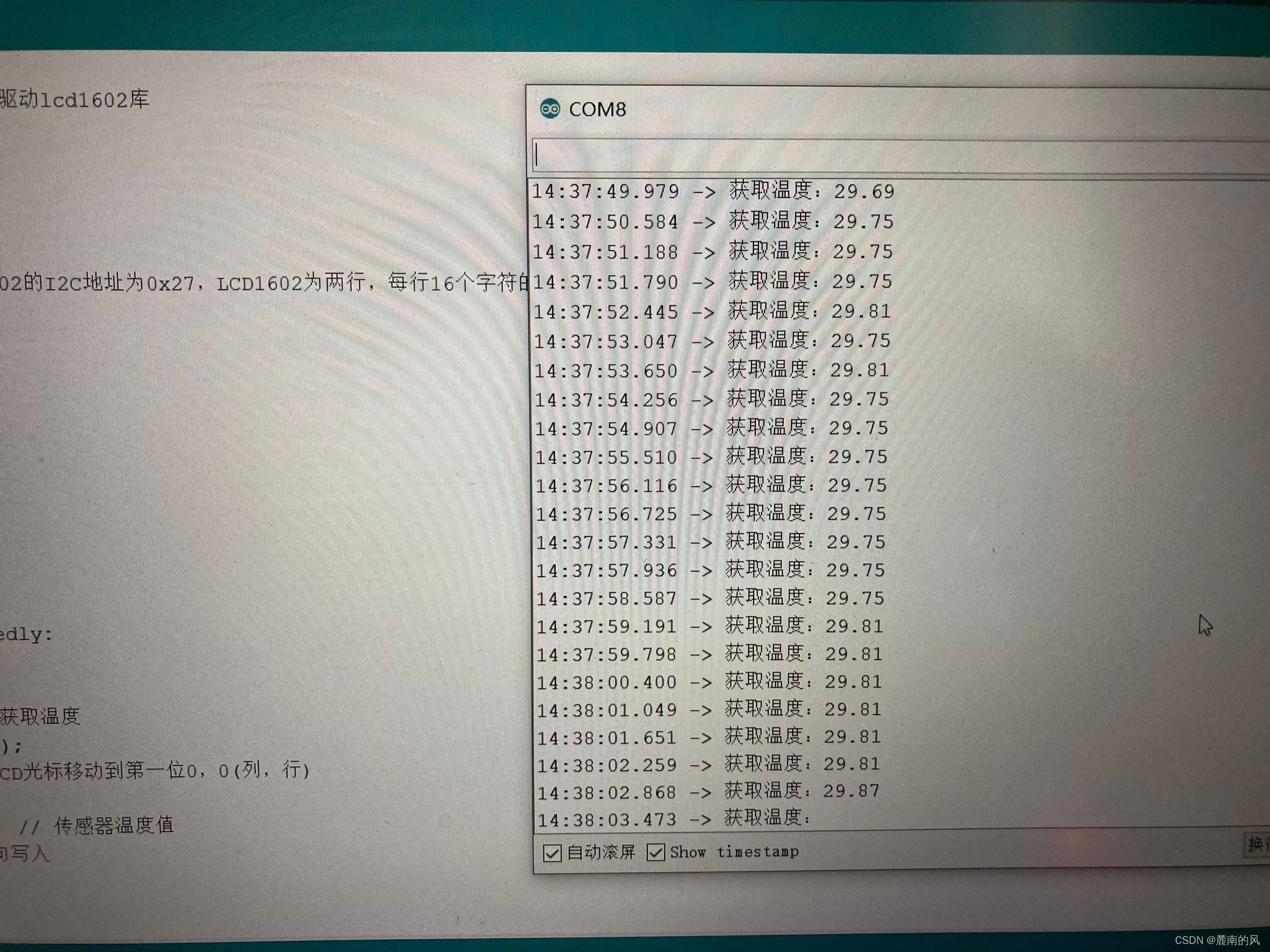
Arduino+ds18b20 temperature sensor (buzzer alarm) +lcd1602 display (IIC drive)

2.初识C语言(2)
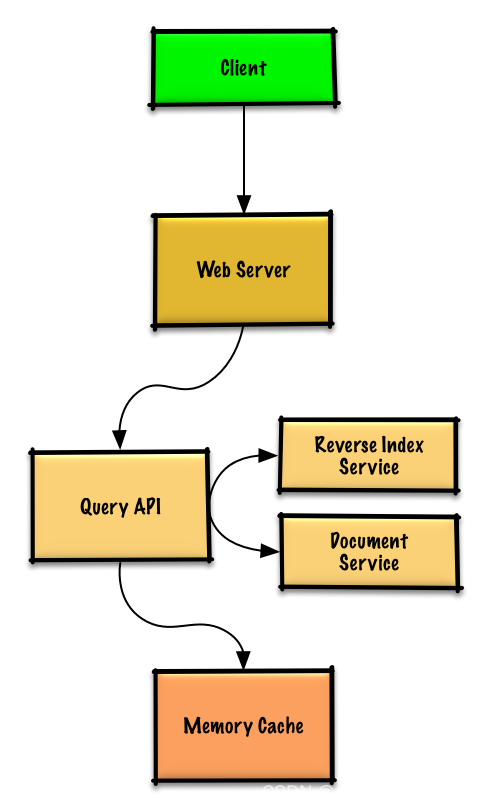
系统设计学习(二)Design a key-value cache to save the results of the most recent web server queries

Design a key value cache to save the results of the most recent Web server queries
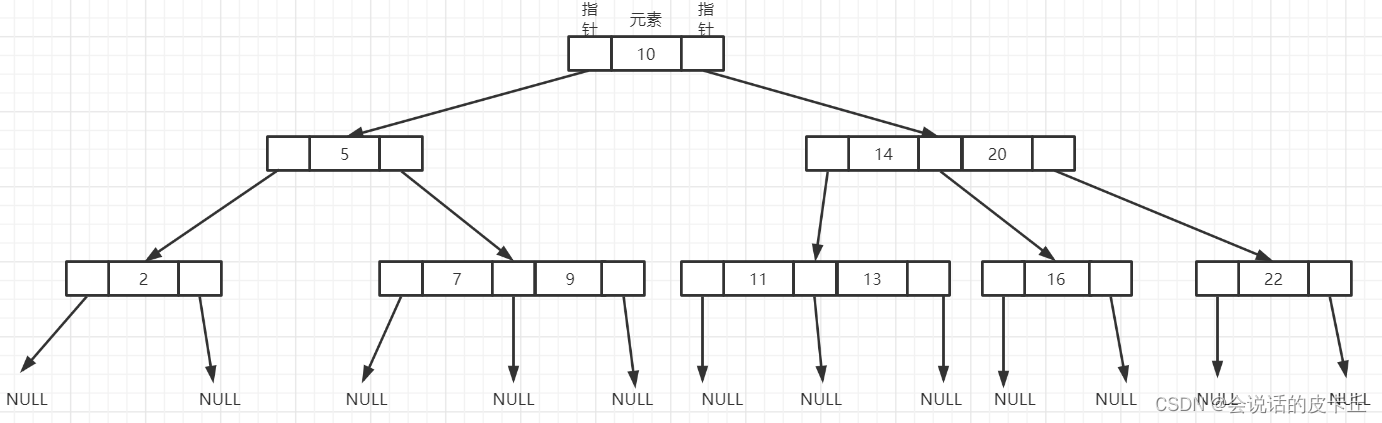
Differences and application scenarios between MySQL index clock B-tree, b+tree and hash indexes

8.C语言——位操作符与位移操作符

TYUT太原理工大学2022数据库题库选择题总结
十分鐘徹底掌握緩存擊穿、緩存穿透、緩存雪崩
IPv6 experiment
随机推荐
string
A brief introduction to the database of tyut Taiyuan University of technology in previous years
Arduino+ds18b20 temperature sensor (buzzer alarm) +lcd1602 display (IIC drive)
Atomic and nonatomic
arduino+DS18B20温度传感器(蜂鸣器报警)+LCD1602显示(IIC驱动)
Comparison between FileInputStream and bufferedinputstream
抽象类和接口
凡人修仙学指针-1
First acquaintance with C language (Part 1)
更改VS主题及设置背景图片
Questions and answers of "basic experiment" in the first semester of the 22nd academic year of Xi'an University of Electronic Science and technology
最新坦克大战2022-全程开发笔记-3
Arduino+ water level sensor +led display + buzzer alarm
学编程的八大电脑操作,总有一款你不会
4.30 dynamic memory allocation notes
西安电子科技大学22学年上学期《信号与系统》试题及答案
MySQL 30000 word essence summary + 100 interview questions, hanging the interviewer is more than enough (Collection Series
Redis介绍与使用
Voir ui plus version 1.3.1 pour améliorer l'expérience Typescript
[中国近代史] 第六章测验