当前位置:网站首页>LIS 最长上升子序列问题(动态规划、贪心+二分)
LIS 最长上升子序列问题(动态规划、贪心+二分)
2022-07-07 11:10:00 【-YIN】
参考一篇大佬博客学习到的解题方法:LIS(最长上升子序列)问题的三种求解方法以及一些例题
最长上升子序列
首先要理解两个概念:
1. 子串
串中任意个连续的字符组成的子序列称为该串的子串
对于一个字符串变量,例如"abcde",它的子串就是像"abc"这样可以从中找到的连续的字符串。字符串"abcde"本身也属于它本身最长的子串。
子串个数计算:
abc 的子串:a、 b、 c、 ab、 bc 、abc、/0共(3+2+1+1)个,
若字符串的长度为 n,则子串的个数就是[n*(n+1)/2+1]个, 例如:"software"中子串的个数就是8+7+…+1+1=37个,即为37个。
特别的!对于有连续相同的子串(例如:AAABBBCCC)这样的子串的计算方法是n(n+1)/2+1-重复子串
2. 子序列
子序列就是在原来序列中找出一部分组成的序列, 不一定连续但先后顺序与原序列一致
如 “abcdefg” 中,acd,bdf 属于它的子序列,而 bac,dbfg 则不是,因为它们与字符串的字符顺序不一致。
区别:
最长公共子序列(LCS) 是一个在一个序列集合中(通常为两个序列)用来查找所有序列中最长子序列的问题。这与查找最长公共子串的问题不同的地方是:子序列不需要在原序列中占用连续的位置; 而最长公共子序列必须连续。
LIC定义
最长上升子序列(Longest Increasing Subsequence),简称LIS,是一个在一个序列集合中(通常为两个序列)用来查找所有序列中最长子序列的问题。也有些情况求的是最长非降序子序列,二者区别就是序列中是否可以有相等的数。
假设我们有一个序列 b i,当b1 < b2 < … < bn 的时候,我们称这个序列是上升的。对于给定的一个序列(a1, a2, …, aN),我们也可以从中得到一些上升的子序列(ai1, ai2, …, aiK),这里1 <= i1 < i2 < … < iK <= N,但必须按照从前到后的顺序。比如,对于序列(1, 7, 3, 5, 9, 4, 8),我们就会得到一些上升的子序列,如(1, 7, 9), (3, 4, 8), (1, 3, 5, 8)等等,而这些子序列中最长的(如子序列(1, 3, 5, 8) ),它的长度为4,因此该序列的最长上升子序列长度为4。
如果光看定义的话会发现比较难理解,所以先看个例题
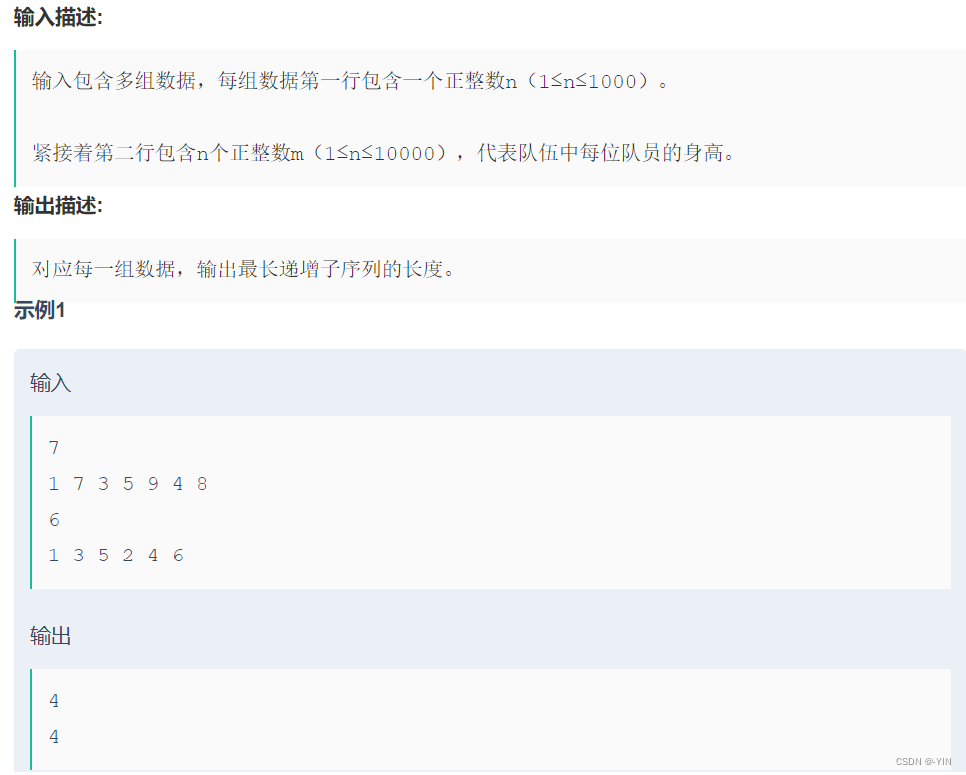
例题:广场舞队伍
题目链接:
来源:牛客网
广场上站着一支队伍,她们是来自全国各地的扭秧歌代表队,现在有她们的身高数据,请你帮忙找出身高依次递增的子序列。 例如队伍的身高数据是(1、7、3、5、9、4、8),其中依次递增的子序列有(1、7),(1、3、5、9),(1、3、4、8)等,其中最长的长度为4。
分析:对于固定的数组,虽然LIS序列不一定唯一,但LIS的长度是唯一的。
从题目给出的例子来看
动态规划
时间复杂度 O(n2), 空间复杂度 O(n)
给出与序列长度大小相等的 dp 数组,下标 i 表示 以 arr[ i ] 结尾的 LIS 的长度
状态转移方程:dp[i] = max( dp[i],dp[j] + 1)
d(i) 就是找以A[ i ]结尾的最长子序列,在 A[ i ] 之前的最长上升子序列+1,即前 i 个数的 LIS 长度 + 1。当 A[ i ] 之前没有比 A[ i ] 更小的数时,d(i) = 1。所有的d(i)里面最大的那个就是最长上升子序列。
其实说的通俗点,就是每次都向前找比它小的数与比它大的数的位置,将第一个比它大的替换掉,这样操作虽然LIS序列的具体数字可能会变,但是很明显LIS长度还是不变的
#include <iostream>
#include <vector>
using namespace std;
// 动态规划
size_t MostAddSub(vector<int>& v){
vector<int> dp(v.size(), 1);
size_t sum = 1;
for(size_t i = 0; i < v.size(); ++i){
for(size_t j = 0; j < i; ++j){
if(v[i] > v[j])
dp[i] = dp[i] > dp[j]+1 ? dp[i] : dp[j]+1;
}
sum = sum > dp[i] ? sum : dp[i];
}
return sum;
}
int main()
{
int n;
while (cin >> n){
vector<int> v(n);
for (int i = 0; i < n; ++i)
cin >> v[i];
cout << MostAddSub(v) << endl;
}
return 0;
}
贪心+二分法
时间复杂度 O(nlogn), 空间复杂度 O(n)
大佬文章中的解释
新给一个 low 数组,low [ i ]表示长度为 i 的LIS结尾元素的最小值。对于一个上升子序列,显然其结尾元素越小,越有利于在后面接其他的元素,也就越可能变得更长。因此,我们只需要维护 low 数组,对于每一个a[ i ],如果a[ i ] > low [当前最长的LIS长度],就把 a [ i ]接到当前最长的LIS后面,即low [++当前最长的LIS长度] = a [ i ]。
对于每一个a [ i ],如果a [ i ]能接到 LIS 后面,就接上去;否则,就用 a [ i ] 取更新 low 数组。具体方法是,在low数组中二分查找找到第一个大于等于a [ i ]的元素low [ j ],用a [ i ]去更新 low [ j ]。如果从头到尾扫一遍 low 数组的话,时间复杂度仍是O(n^2)。我们注意到 low 数组内部一定是单调不降的,所有我们可以二分 low 数组,找出第一个大于等于a[ i ]的元素。二分一次 low 数组的时间复杂度的O(lgn),所以总的时间复杂度是O(nlogn)。
不得不说,有二分的地方二分的边界永远是最恶心的最难搞的,整体思路不难。
- 新建一个长度为 n+1 的数组 low ,数组 low[i]表示长度为 i 的最长上升子序列的末尾元素的最小值。
即数组 1,2,3,4,5,6中长度为3的上升子序列可以为 1,2,3也可以为 2,3,4等等,但是d[3]=3,即子序列末尾元素最小为3(1,2,3)
- low 数组具有单调性,即表明:(1)可以使用二分法;(2)数组 low 的长度即为最长子序列的长度;
我们接着需要证明数组 low 具有单调性,即证明 i<j 时,low [i]<low [j],使用反证法,假设存在k<j时,low [k]>low [j],但在长度为j,末尾元素为low [j]的子序列A中,将后 j-i 个元素减掉,可以得到一个长度为 i 的子序列B,其末尾元素 t1 必然小于low [j](因为在子序列A中,t1的位置上在d[j]的后面),而我们假设数组 low 必须符合表示长度为 i 的最长上升子序列的末尾元素的最小值,此时长度为i的子序列的末尾元素t1 < low [j] < low [k],即t1<low [k],所以low [k]不是最小的,与题设相矛盾,因此可以证明其单调性
// 二分查找v中第一个>=num的元素下标
size_t Binary_search(vector<int>& low, int right, int num){
int left = 1, mid;
while (left <= right){
mid = ((right-left)>>1)+left;
if (low[mid] < num)
left = mid + 1;
else
right = mid - 1;
}
return left;
}
// 计算最大升序子序列长度
size_t FIS(vector<int>& v){
vector<int> low(v.size()+1, 0);
size_t retLen = 1;
low[retLen] = v[0];
for(size_t i = 1; i < v.size(); ++i){
if(low[retLen] < v[i])
low[++retLen] = v[i];
else
low[Binary_search(low, retLen, v[i])] = v[i];//二分查找
}
return retLen;
}
利用二分查找接口:
或着可以使用 STL库中 <algorithm> 中提供的二分查找值位置(lower_bound())的方法
STL中关于二分查找的函数有三个
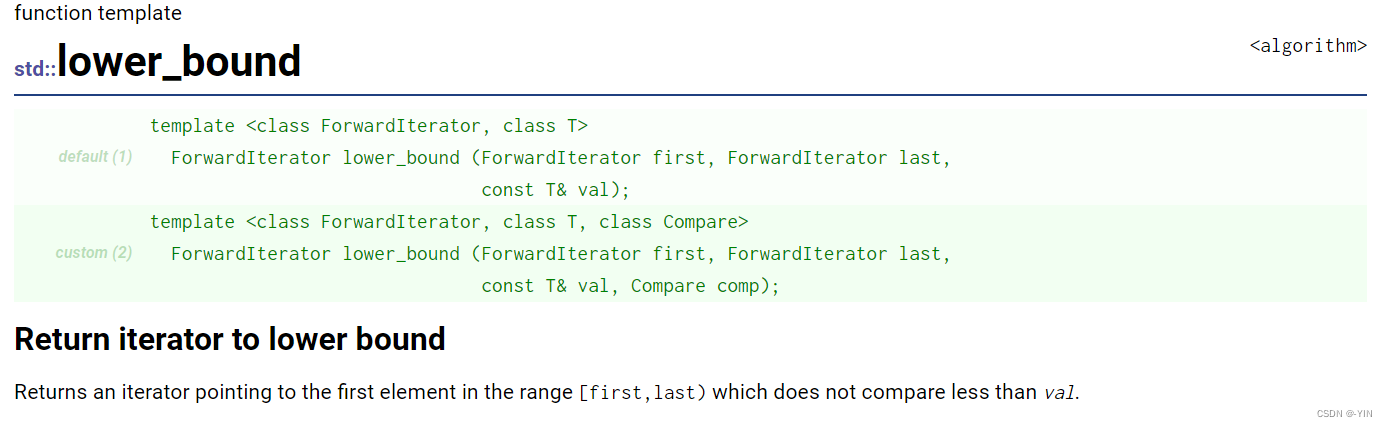
lower_bound、upper_bound、binary_search。这三个函数都运用于有序区间(当然这也是运用二分查找的前提)。
其中如果寻找的 val 存在,那么lower_bound返回一个迭代器指向其中第一个这个元素。upper_bound返回一个迭代器指向其中最后一个这个元素的下一个位置(明确点说就是返回在不破坏顺序的情况下,可插入value的最后一个位置)。如果寻找的value不存在,那么lower_bound和upper_bound都返回“假设这样的元素存在时应该出现的位置”。
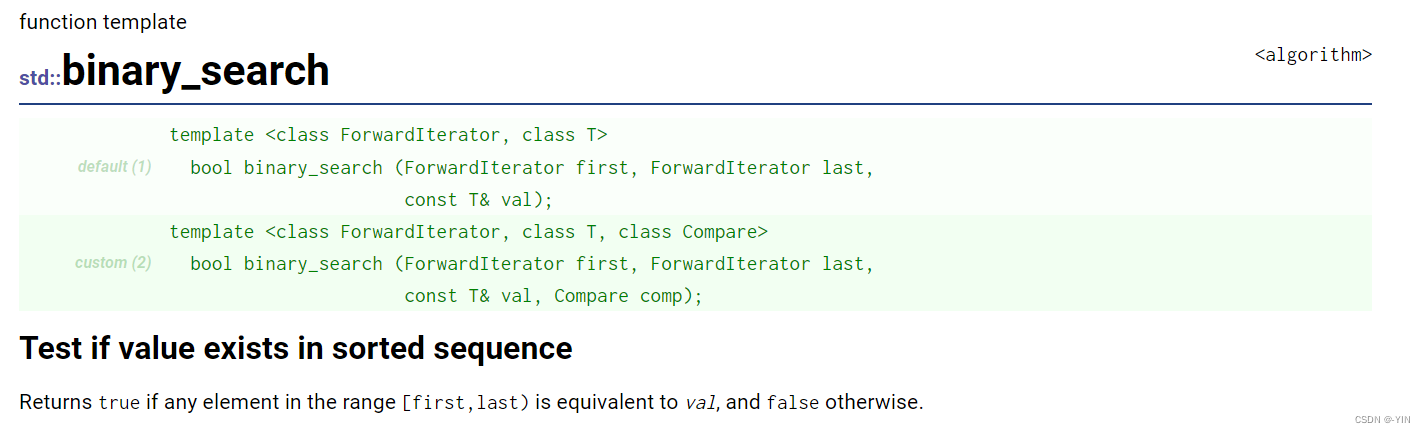
binary_search试图在已排序的[first,last)中寻找元素val,若存在就返回true,若不存在则返回false。返回单纯的布尔值也许不能满足需求,而lower_bound、upper_bound能提供额外的信息。事实上由源码可知binary_search便是利用lower_bound求出元素应该出现的位置,然后再比较该位置 的值与value的值。该函数有两个版本一个是operator< ,另外一个是利用仿函数comp进行比较。
binary_search 这个方法是判断val是否在序列中,返回的是bool值,这个题没法使用
详见:STL二分查找——lower_bound 、upper_bound 、binary_search
int lengthOfLIS(vector<int>& nums) {
vector<int> low;
low.push_back(nums[0]);
for(int i = 1; i < nums.size(); ++i){
if(low.back() < nums[i])
low.push_back(nums[i]);
else{
// lower_bound 返回找到位置的迭代器
*(lower_bound(low.begin(), low.end(), nums[i]))=nums[i];
}
}
return low.size();
}
边栏推荐
- Leetcode skimming: binary tree 20 (search in binary search tree)
- HZOJ #236. Recursive implementation of combinatorial enumeration
- HZOJ #240. Graphic printing IV
- 企业级自定义表单引擎解决方案(十二)--体验代码目录结构
- The difference between cache and buffer
- 高瓴投的澳斯康生物冲刺科创板:年营收4.5亿 丢掉与康希诺合作
- [binary tree] delete points to form a forest
- Cookie and session comparison
- 线程池拒绝策略最佳实践
- 3D content generation based on nerf
猜你喜欢
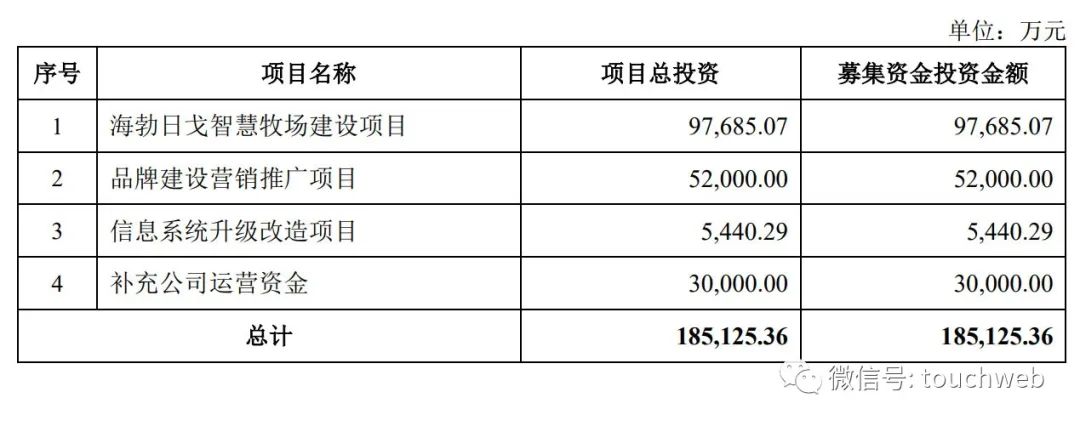
认养一头牛冲刺A股:拟募资18.5亿 徐晓波持股近40%

共创软硬件协同生态:Graphcore IPU与百度飞桨的“联合提交”亮相MLPerf
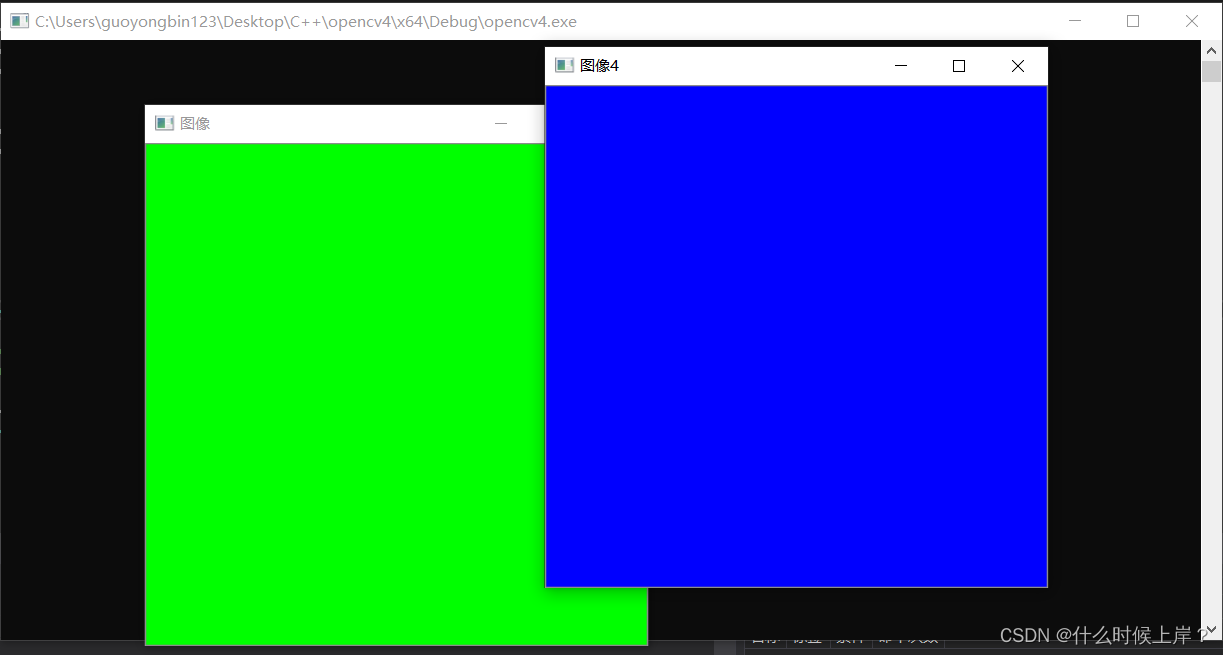
Creation and assignment of graphic objects
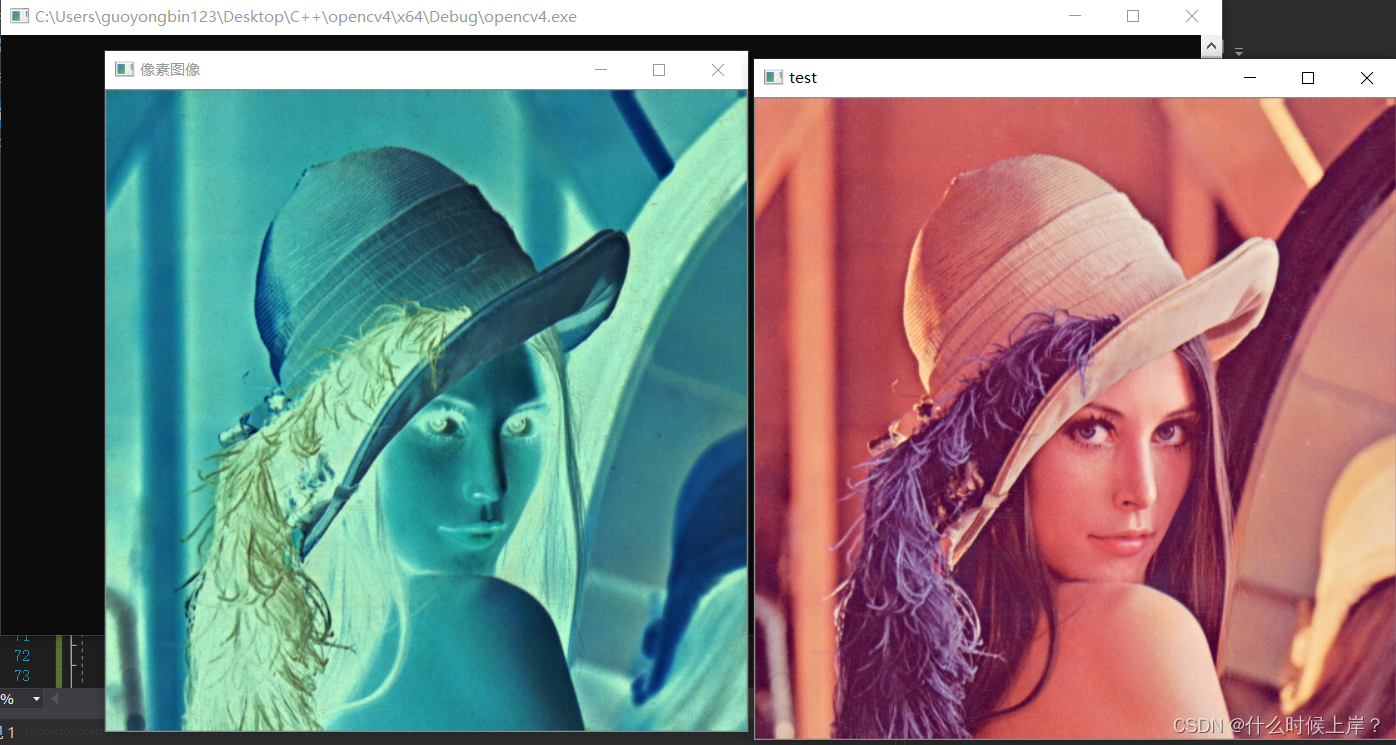
Image pixel read / write operation

Leetcode brush questions: binary tree 19 (merge binary tree)
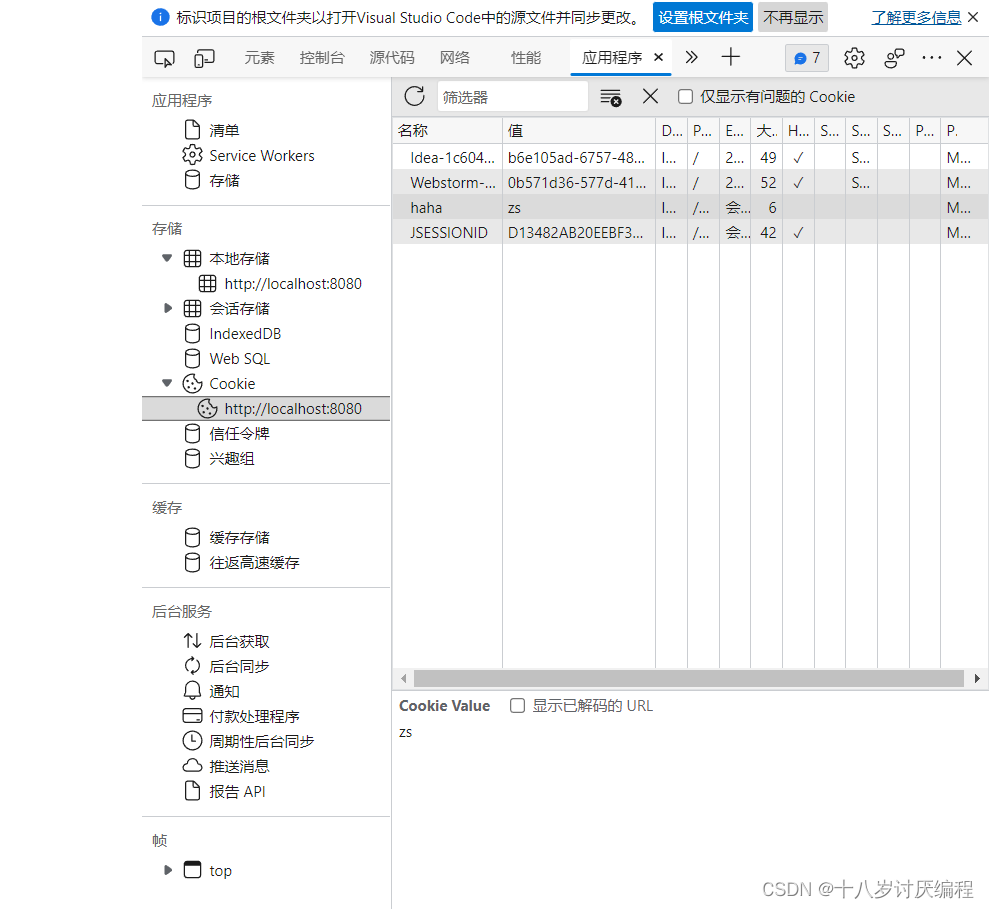
Cookie

将数学公式在el-table里面展示出来
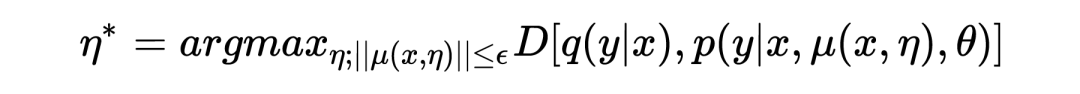
ICLR 2022 | pre training language model based on anti self attention mechanism

2022 practice questions and mock examination of the third batch of Guangdong Provincial Safety Officer a certificate (main person in charge)
2022 polymerization process test question simulation test question bank and online simulation test
随机推荐
Day26 IP query items
PCAP学习笔记二:pcap4j源码笔记
Query whether a field has an index with MySQL
How to continue after handling chain interruption / sub chain error removed from scheduling
Unity 构建错误:当前上下文中不存在名称“EditorUtility”
Find ID value MySQL in string
HZOJ #235. Recursive implementation of exponential enumeration
谷歌浏览器如何重置?谷歌浏览器恢复默认设置?
PACP学习笔记一:使用 PCAP 编程
@Resource和@Autowired的区别?
日本政企员工喝醉丢失46万信息U盘,公开道歉又透露密码规则
HZOJ #240. Graphic printing IV
事务的七种传播行为
Leetcode question brushing: binary tree 26 (insertion operation in binary search tree)
Four functions of opencv
RecyclerView的数据刷新
Leetcode skimming: binary tree 21 (verifying binary search tree)
将数学公式在el-table里面展示出来
明星企业普渡科技大裁员:曾募资超10亿 腾讯红杉是股东
为租客提供帮助