Some understandings of tree LSTM and DGL code implementation

Preface

Tree-LSTM In fact, I studied it a long time ago , That should be my first time to learn DGL When . Because a tree is a special kind of graph , It can also be regarded as the basic operation of neural network in my primer , I vaguely remember that I worked on the model for a long time …

Tree-LSTM

Tree-LSTM It is a tree structure LSTM, To be able to improve LSTM Parallel speed of computation , At the same time, it can integrate the relevant information of dependency tree or syntax tree , So as to achieve a better effect of sentence modeling .

Tree-LSTM There are two forms , One is N-ary Tree-LSTM The other is Child-sum Tree-LSTM, The former can record timing information, but it has characteristic restrictions on the number of child nodes , The latter will lose location information , But there is no requirement for the number of child nodes .

LSTM

In understanding two Tree-LSTM front , We can review our classic LSTM: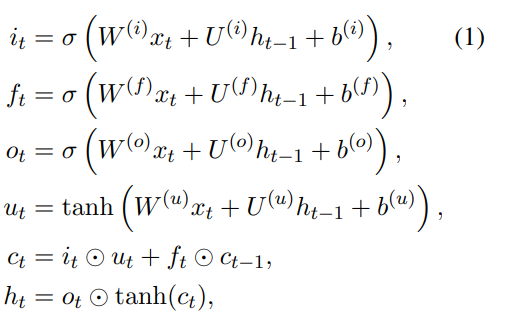

among ：
σ（）、tanh（） Is the activation function
i_t Is to input the information we get ,x^t It's the characteristics of input ,W⁽ⁱ⁾ Is the transformation matrix corresponding to the input characteristics of the input gate ,h_t-1 Is the hidden layer of the previous state U⁽ⁱ⁾ Is the transformation matrix of the hidden layer of the input gate ,b⁽ⁱ⁾ Is the offset of the input gate

f_t Is the information obtained by forgetting the door ,x^t It's the characteristics of input ,W^(f) Is the transformation matrix corresponding to the input characteristics of the forgetting gate ,h_t-1 Is the hidden layer of the previous state U^(f) Is the transformation matrix of the hidden layer of the forgetting gate ,b^(f) For forgetting the offset of the door

o_t It is the information obtained by the output gate ,x^t It's the characteristics of input ,W^(o) Is the transformation matrix corresponding to the input characteristics of the output gate ,h_t-1 Is the hidden layer of the previous state U^(o) Is the transformation matrix of the hidden layer of the output gate ,b^(o) For forgetting the offset of the door

c_t For the current cell state ,⨀ Representative dot product , That is, the corresponding elements of the matrix are multiplied

h_t Is the updated hidden layer

in general , The formula is relatively simple , Because no Σ Summation symbol or something , It's easy to understand the calculation process of the formula .

N-ary Tree-LSTM

N-ary Tree-LSTM That is to say N Children node Tree-LSTM, It is characterized by better retention of timing information , However, there are restrictions on the number of child nodes , Therefore, this kind of input is generally binary tree structure , Because the calculation is relatively simple .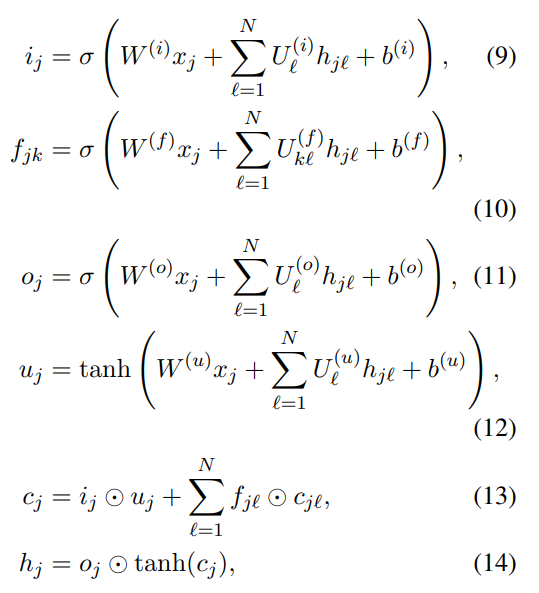

N-ary Tree-LSTM And classic LSTM Just a few more Σ Summation symbol .

If N=2, That means that the number of child nodes of each parent node is 2, Then input gate 、 Output gate 、 There are two in the forgetting door U To perform a linear transformation on the hidden layer corresponding to the two child nodes at the previous moment , Then sum it , Because this operation corresponds to the left and right children , Therefore, the timing information can be recorded . because N=2 It is preset , If there are three child nodes in your data , Then you have to report an error .

Let's take an example to compare the image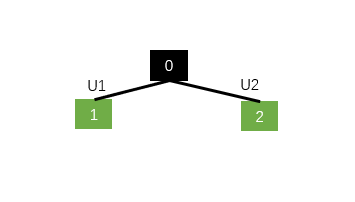

for example N=2,0 Parent node , that N-ary Tree-LSTM At the child node 1 and 2 A hidden layer transformation matrix is set in the three doors in the position of U1 and U2, The left node is the same as U1 Calculation , The right node is the same as U2 Calculation , This ensures that the location information can be preserved , However, it cannot solve the situation that the data contains trigeminal and above .

Child-sum Tree-LSTM

Child-sum Tree-LSTM It's simpler , seeing the name of a thing one thinks of its function , It is to sum the hidden layers of child nodes and then update the hidden layers of parent nodes .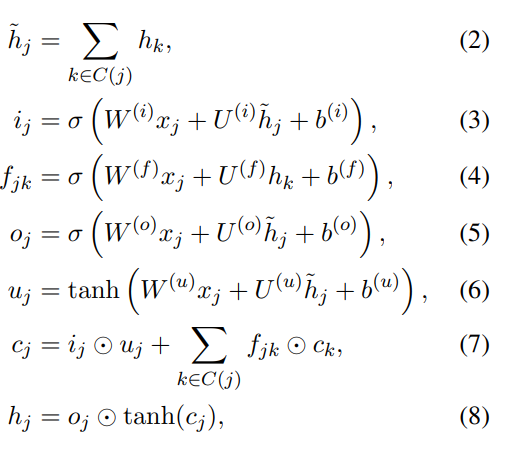

contrast N-ary Tree-LSTM One of the three doors can be found Σ The summation symbol is gone , because （2） Sum the hidden layers of child nodes directly , Write it down as $\tilde{h}$_j, Then use it to enter three doors for calculation . Because here is the sum operation , Then the number of child nodes is unlimited , Because after summing, there is only one , Only one of the three doors needs to be set U that will do , But the disadvantage is , After the sum , The location information of the child node is lost .

And here the forgetting gate is to seek a forgetting information for each child node , It's just shared parameters U^(f)

You can also take an example , For example, at this time N=3
If it is N-ary Tree-LSTM: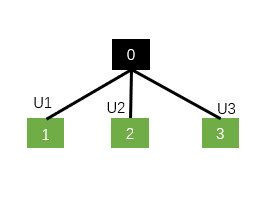

It should correspond to three groups .
If it is Child-sum Tree-LSTM:

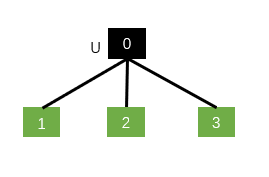
You just need one , Because the child nodes are summed .

DGL Code implementation

N-ary Tree-LSTM

This code comes entirely from DGL Official website . Here is an emotion classification task that predicts each node .

from collections import namedtuple

import dgl
from dgl.data.tree import SSTDataset


SSTBatch = namedtuple('SSTBatch', ['graph', 'mask', 'wordid', 'label'])

# Each sample in the dataset is a constituency tree. The leaf nodes
# represent words. The word is an int value stored in the "x" field.
# The non-leaf nodes have a special word PAD_WORD. The sentiment
# label is stored in the "y" feature field.
trainset = SSTDataset(mode='tiny')  # the "tiny" set has only five trees
tiny_sst = trainset.trees
num_vocabs = trainset.num_vocabs
num_classes = trainset.num_classes

vocab = trainset.vocab # vocabulary dict: key -> id
inv_vocab = {
    v: k for k, v in vocab.items()} # inverted vocabulary dict: id -> word

a_tree = tiny_sst[0]
for token in a_tree.ndata['x'].tolist():
    if token != trainset.PAD_WORD:
        print(inv_vocab[token], end=" ")

import torch as th
import torch.nn as nn

class TreeLSTMCell(nn.Module):
    def __init__(self, x_size, h_size):
        super(TreeLSTMCell, self).__init__()
        self.W_iou = nn.Linear(x_size, 3 * h_size, bias=False)
        self.U_iou = nn.Linear(2 * h_size, 3 * h_size, bias=False)
        self.b_iou = nn.Parameter(th.zeros(1, 3 * h_size))
        self.U_f = nn.Linear(2 * h_size, 2 * h_size)

    def message_func(self, edges):
        return {
    'h': edges.src['h'], 'c': edges.src['c']}

    def reduce_func(self, nodes):
        # concatenate h_jl for equation (1), (2), (3), (4)
        h_cat = nodes.mailbox['h'].view(nodes.mailbox['h'].size(0), -1)
        # equation (2)
        f = th.sigmoid(self.U_f(h_cat)).view(*nodes.mailbox['h'].size())
        # second term of equation (5)
        c = th.sum(f * nodes.mailbox['c'], 1)
        return {
    'iou': self.U_iou(h_cat), 'c': c}

    def apply_node_func(self, nodes):
        # equation (1), (3), (4)
        iou = nodes.data['iou'] + self.b_iou
        i, o, u = th.chunk(iou, 3, 1)
        i, o, u = th.sigmoid(i), th.sigmoid(o), th.tanh(u)
        # equation (5)
        c = i * u + nodes.data['c']
        # equation (6)
        h = o * th.tanh(c)
        return {
    'h' : h, 'c' : c}


class TreeLSTM(nn.Module):
    def __init__(self,
                 num_vocabs,
                 x_size,
                 h_size,
                 num_classes,
                 dropout,
                 pretrained_emb=None):
        super(TreeLSTM, self).__init__()
        self.x_size = x_size
        self.embedding = nn.Embedding(num_vocabs, x_size)
        if pretrained_emb is not None:
            print('Using glove')
            self.embedding.weight.data.copy_(pretrained_emb)
            self.embedding.weight.requires_grad = True
        self.dropout = nn.Dropout(dropout)
        self.linear = nn.Linear(h_size, num_classes)
        self.cell = TreeLSTMCell(x_size, h_size)

    def forward(self, batch, h, c):
        """Compute tree-lstm prediction given a batch. Parameters ---------- batch : dgl.data.SSTBatch The data batch. h : Tensor Initial hidden state. c : Tensor Initial cell state. Returns ------- logits : Tensor The prediction of each node. """
        g = batch.graph
        # to heterogenous graph
        g = dgl.graph(g.edges())
        # feed embedding
        embeds = self.embedding(batch.wordid * batch.mask)
        g.ndata['iou'] = self.cell.W_iou(self.dropout(embeds)) * batch.mask.float().unsqueeze(-1)
        g.ndata['h'] = h
        g.ndata['c'] = c
        # propagate
        dgl.prop_nodes_topo(g,
                            message_func=self.cell.message_func,
                            reduce_func=self.cell.reduce_func,
                            apply_node_func=self.cell.apply_node_func)
        # compute logits
        h = self.dropout(g.ndata.pop('h'))
        logits = self.linear(h)
        return logits


from torch.utils.data import DataLoader
import torch.nn.functional as F

device = th.device('cpu')
# hyper parameters
x_size = 256
h_size = 256
dropout = 0.5
lr = 0.05
weight_decay = 1e-4
epochs = 10

# create the model
model = TreeLSTM(trainset.num_vocabs,
                 x_size,
                 h_size,
                 trainset.num_classes,
                 dropout)
print(model)

# create the optimizer
optimizer = th.optim.Adagrad(model.parameters(),
                          lr=lr,
                          weight_decay=weight_decay)

def batcher(dev):
    def batcher_dev(batch):
        batch_trees = dgl.batch(batch)
        return SSTBatch(graph=batch_trees,
                        mask=batch_trees.ndata['mask'].to(device),
                        wordid=batch_trees.ndata['x'].to(device),
                        label=batch_trees.ndata['y'].to(device))
    return batcher_dev

train_loader = DataLoader(dataset=tiny_sst,
                          batch_size=5,
                          collate_fn=batcher(device),
                          shuffle=False,
                          num_workers=0)

# training loop
for epoch in range(epochs):
    for step, batch in enumerate(train_loader):
        g = batch.graph
        n = g.number_of_nodes()
        h = th.zeros((n, h_size))
        c = th.zeros((n, h_size))
        logits = model(batch, h, c)
        logp = F.log_softmax(logits, 1)
        loss = F.nll_loss(logp, batch.label, reduction='sum')
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()
        pred = th.argmax(logits, 1)
        acc = float(th.sum(th.eq(batch.label, pred))) / len(batch.label)
        print("Epoch {:05d} | Step {:05d} | Loss {:.4f} | Acc {:.4f} |".format(
            epoch, step, loss.item(), acc))

Child-sum Tree-LSTM

You can understand N-ary Look again. Child-sum Of , Not so much .

import torch as th
import torch.nn as nn
class ChildSumTreeLSTMCell(nn.Module):
    def __init__(self, x_size, h_size):
        super(ChildSumTreeLSTMCell, self).__init__()
        self.W_iou = nn.Linear(x_size, 3 * h_size, bias=False)
        self.U_iou = nn.Linear(h_size, 3 * h_size, bias=False)
        self.b_iou = nn.Parameter(th.zeros(1, 3 * h_size))
        self.U_f = nn.Linear(h_size, h_size)

    def message_func(self, edges):
        return {
    'h': edges.src['h'], 'c': edges.src['c']}

    def reduce_func(self, nodes):
        h_tild = th.sum(nodes.mailbox['h'], 1)
        f = th.sigmoid(self.U_f(nodes.mailbox['h']))
        c = th.sum(f * nodes.mailbox['c'], 1)
        return {
    'iou': self.U_iou(h_tild), 'c': c}

    def apply_node_func(self, nodes):
        iou = nodes.data['iou'] + self.b_iou
        i, o, u = th.chunk(iou, 3, 1)
        i, o, u = th.sigmoid(i), th.sigmoid(o), th.tanh(u)
        c = i * u + nodes.data['c']
        h = o * th.tanh(c)
        return {
    'h': h, 'c': c}



class TreeLSTM(nn.Module):
    def __init__(self,
                 num_vocabs,
                 x_size,
                 h_size,
                 num_classes,
                 dropout,
                 pretrained_emb=None):
        super(TreeLSTM, self).__init__()
        self.x_size = x_size
        self.embedding = nn.Embedding(num_vocabs, x_size)
        if pretrained_emb is not None:# Here you can use the pre training word vector 
            print('Using glove')
            self.embedding.weight.data.copy_(pretrained_emb)
            self.embedding.weight.requires_grad = True
        self.dropout = nn.Dropout(dropout)
        self.linear = nn.Linear(h_size, num_classes)
        self.cell = ChildSumTreeLSTMCell(x_size, h_size)

    def forward(self, batch, h, c):
        """Compute tree-lstm prediction given a batch. Parameters ---------- batch : dgl.data.SSTBatch The data batch. h : Tensor Initial hidden state. c : Tensor Initial cell state. Returns ------- logits : Tensor The prediction of each node. """
        # print("batch", batch)
        g = batch.graph
        # print("g", g)
        # to heterogenous graph
        g = dgl.graph(g.edges())
        # feed embedding
        embeds = self.embedding(batch.wordid * batch.mask)
        # Leaf nodes have no depth , therefore message_func and reduce_func Can be ignored , direct apply_node_func

        g.ndata['iou'] = self.cell.W_iou(self.dropout(embeds)) * batch.mask.float().unsqueeze(-1)
        g.ndata['h'] = h
        g.ndata['c'] = c
        g.ndata['node_pos'] = batch.node_pos
        # print(type(batch.wordid))
        # prop_nodes_topo Message passing is based on the topology order we specify 
        dgl.prop_nodes_topo(g,
                            message_func=self.cell.message_func,
                            reduce_func=self.cell.reduce_func,
                            apply_node_func=self.cell.apply_node_func)
        # compute logits
        # print("after_prop_nodes_topo", g)
        h = self.dropout(g.ndata.pop('h'))
        pos = g.ndata["node_pos"]
        pos_sen = torch.nonzero(pos==0).squeeze()  # 0 The location of is the root node 
        sen_hidden = h[pos_sen]

        logits = self.linear(sen_hidden)
        return logits

child_sum_Tree_LSTM = TreeLSTM(100, 50, 50, 2, 0.2)
print(child_sum_Tree_LSTM)

Reference resources

2015-Tree-LSTM-Improved Semantic Representations From Tree-Structured Long Short-Term Memory Networks
https://docs.dgl.ai/tutorials/models/2_small_graph/3_tree-lstm.html#sphx-glr-tutorials-models-2-small-graph-3-tree-lstm-py