windows10 tensorflow（二）原理实战之回归分析，深度学习框架（梯度下降法求解回归参数）

windows10 tensorflow（二）原理实战之回归分析，深度学习框架（梯度下降法求解回归参数）
TF数据生成方式：参考TF数据生成12法
TF基本原理与概念理解： tensorflow（一）windows 10 64位安装tensorflow1.4与基本概念解读tf.global_variables_initializer
模型：

一个简单的线性回归y = W * x + b，采用numpy构建完整回归数据，并增加干扰噪声

import numpy as np
#建立一个一元线性回归方程y=0.1x1+0.3  ,同时一个正太分布偏差np.random.normal(0.0,0.03)用于见证TF的算法
num_points=1000
vectors_set=[]
for  i in  range(num_points):
    x1=np.random.normal(loc=0.0,scale=0.66)
    y1=x1*0.1+0.3+np.random.normal(0.0,0.03)
    vectors_set.append([x1,y1])
x_data=[v[0] for v in vectors_set]
y_data=[v[1] for v in vectors_set]

Graphic display出数据分布结果

import matplotlib.pyplot as plt
#https://www.cnblogs.com/zqiguoshang/p/5744563.html
##line_styles=['ro-','b^-','gs-','ro--','b^--','gs--']  #set line style
plt.plot(x_data,y_data,'ro',marker='^',c='blue',label='original_data')
plt.legend()
plt.show()

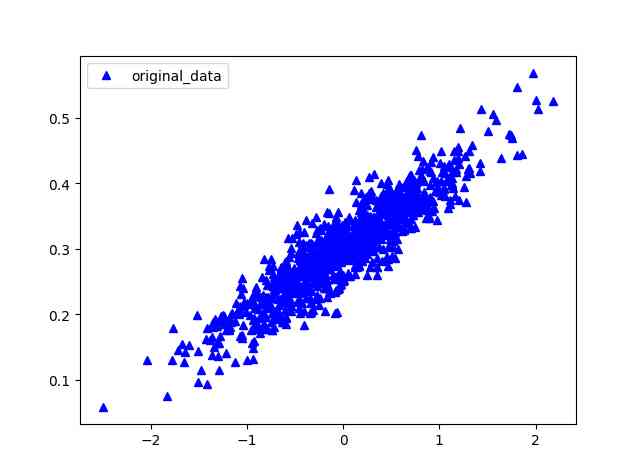
通过TensorFlow代码找到最佳的参数W与b，使的输入数据x_data，生成输出数据y_data，本例中将会一条直线y_data=W*x_data+b。读者知道W会接近0.1，b接近0.3，但是TensorFlow并不知道，它需要自己来计算得到该值。因此采用梯度下降法来迭代求解数据

import tensorflow as tf
import math
#一、创建graph数据
#随便构建一个一元回归方程的参数W与b
W=tf.Variable(tf.random_uniform([1], minval=-1.0, maxval=1.0))
b=tf.Variable(tf.zeros([1]))
y=W*x_data+b

#定义下面的最小化方差
#1.定义最小化误差平方根
loss=tf.reduce_mean(tf.square(y-y_data))
#2.learning_rate=0.5
optimizer=tf.train.GradientDescentOptimizer(learning_rate=0.5)
#3.最优化最小值
train=optimizer.minimize(loss)

#二、初始化变量
init=tf.global_variables_initializer()

#三、启动graph
sess=tf.Session()
sess.run(init)

for step in range(8):
    sess.run(train)
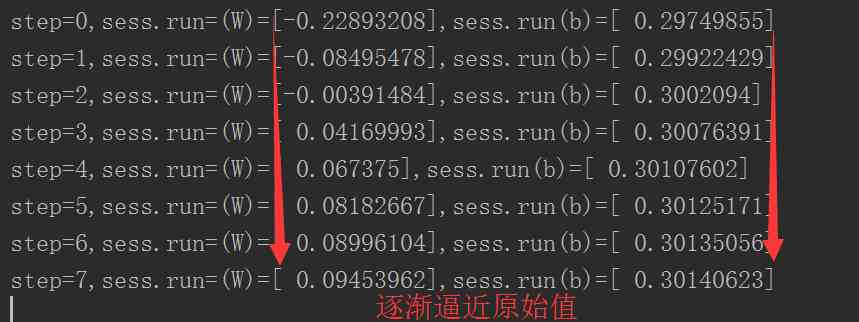
    print("step={},sess.run=(W)={},sess.run(b)={}".format(step,sess.run(W),sess.run(b)))

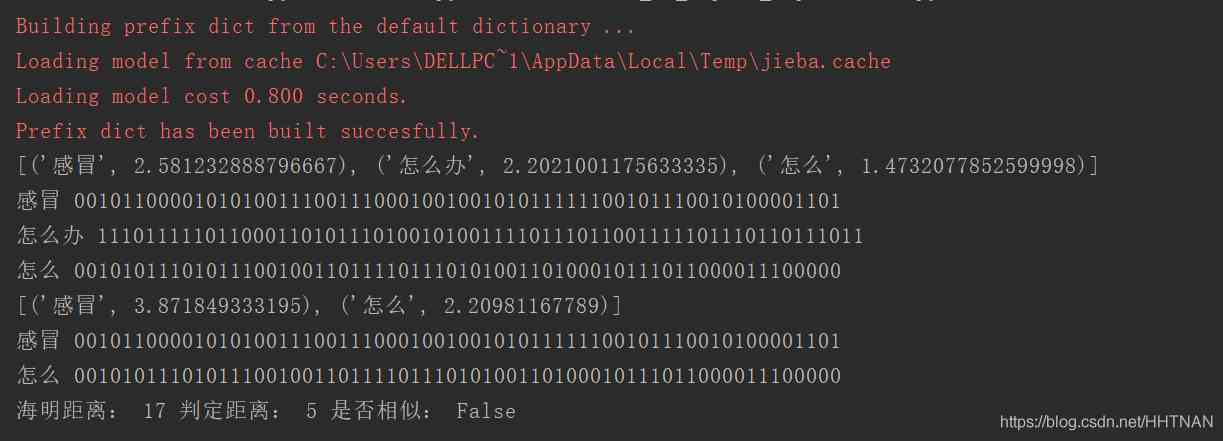
以下是迭代8次的结果。梯度就像一个指南针，指引我们朝着最小的方向前进。为了计算梯度，TensorFlow会对错误函数求导，在我们的例子中就是，算法需要对W和b计算部分导数，以在每次迭代中为前进指明方向。

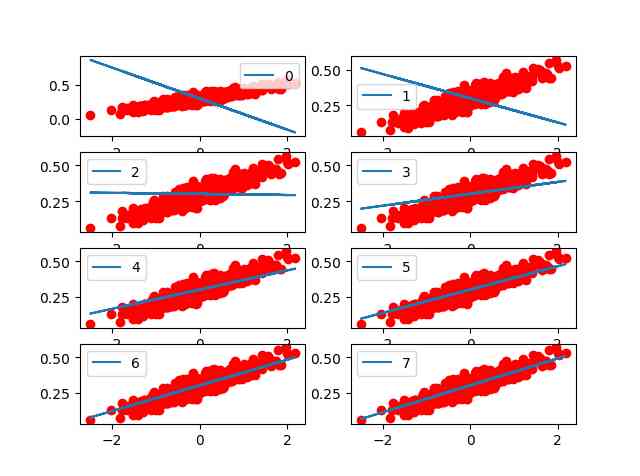
下面是每次迭代的可视化效果图：

#Graphic display
    # print(sub_1+'41')
    #注意：各参数可以用逗号,分隔开。第一个参数代表子图的行数；第二个参数代表该行图像的列数； 第三个参数代表每行的第几个图像，从左致右，从上到下一次增加。
    plt.subplot(4,2,step+1)
	plt.plot(x_data,y_data,'ro')   
	plt.plot(x_data,sess.run(W)*x_data+
	sess.run(b),label=step)
    plt.legend()
plt.show()