Hands on deep learning (46) -- attention mechanism

One 、 Attention mechanism

   The optic nerve in the primate visual system receives a lot of sensory input , Its content is far more than the brain can handle completely . Fortunately, , Not all stimuli have equal effects . The concentration and concentration of consciousness enable primates to attract attention to objects of interest in a complex visual environment , For example, prey and natural enemies . The ability to focus on only a small amount of information has evolutionary significance , Enable mankind to survive and succeed .

   since 19 Since the 20th century , Scientists have been studying attention in the field of cognitive neuroscience . In this chapter , We will first review a popular framework , Explain how to develop attention in a visual scene . Affected by the Attention tips （attention cues） Inspired by the , We will design models that can take advantage of these attention cues . especially 1964 Year of Nadaraya-Waston Nuclear regression （kernel regression） It is with Attention mechanism （attention mechanisms） A simple demonstration of machine learning .

   then , Let's continue with the attention function , They are widely used in the design of attention model of deep learning . say concretely , We will show how to use these functions to design Bahdanau attention .Bahdanau Attention is an attention model with breakthrough value in deep learning , It is bi-directional aligned and differentiable .

   Last , We will describe a system based solely on the attentional mechanism Transformer framework , The architecture uses the latest Long attention （multi-head attention） and Self attention （self-attention） Design . since 2017 The year was conceived ,Transformer It has always been widely used in modern deep learning applications , For example, language 、 Vision 、 Areas of phonics and reinforcement learning .

Two 、 Attention tips

   Attention is a scarce resource ： Now you are reading this blog And ignore the others blog. therefore , Your focus is on opportunity cost （ Similar to money ） To pay for . Attention is scarce in our environment , Information is not . When checking the visual scene , Our optic nerve system receives information about every second $10^8$ position , Far more than the brain can handle completely . Fortunately, , Our ancestors have learned from experience （ Also known as data ） Learn from Not all sensory inputs are the same . Throughout human history , The ability to direct attention to only a small portion of information of interest enables our brain to allocate resources wisely to survive 、 Growth and social , For example, detect natural enemies 、 Food and companionship .

2.1 Attention cues in Biology

   To explain how our attention unfolds in the visual world , A dual component （two-component） The framework of has appeared and become popular . The emergence of this framework can be traced back to 19 century 90 William in the s · James , He is considered to be “ The father of American Psychology ” :cite:James.2007. In this framework , The subjects were based on Involuntary prompt and Autonomous prompt Selectively direct the focus of attention .

   Non autonomous cues are based on the prominence and visibility of objects in the environment . Imagine , There are five items in front of you ： A newspaper 、 A research paper 、 A cup of coffee 、 A notebook and a Book shown in the figure below . Although all paper products are printed in black and white , But the coffee cup is red . let me put it another way , This kind of coffee is essentially prominent and conspicuous in this visual environment , Automatically and involuntarily attract people's attention . So you put fovea（ The macular center with the highest vision ） Take it to the coffee .

   After coffee , You get excited and want to read . So you turn your head , Refocus your eyes , Then read a Book . And The previous prominence led to a preference for coffee , In the case of task dependence, choosing books is controlled by cognition and consciousness , Therefore, attention will be more cautious in assisting selection based on autonomous prompts of variable selection criteria . Driven by the subjective will of the subject , The power of choice is stronger .

2.2 Inquire about 、 Key and value

   Autonomous and involuntary cues explain the way attention unfolds , Inspired by this hint, we will describe the framework for designing attention mechanism in the following , These two attention cues are included in the framework .

   First , Consider a relatively simple situation , That is, only use non autonomous prompts . To bias the choice towards sensory input , We can simply use the parameterized full connection layer , Even nonparametric maximum pooling layer or average pooling layer .

   therefore , By including autonomous prompts, the attention mechanism is distinguished from those of the fully connected layer or the pooled layer . In the context of attention mechanism , We call autonomous prompts Inquire about （Queries）. Given any query , Attention mechanism through Attention pooling （attention pooling） Bias selection to Sensory input （sensory inputs）（ For example, intermediate features represent ）. In the context of attention mechanism , These sensory inputs are called value （Values）. A more popular explanation , Each value is associated with a key （Keys） pairing , This can be imagined as an involuntary prompt for sensory input . We can design attention pools , So that the given query （ Autonomous prompt ） Can be used with the key （ Involuntary prompt ） Interact , This will guide the selection towards values （ Sensory input ）.

   Please note that , There are many alternatives to the design of attention mechanisms . for example , We can design a non differentiable attention model , This model can use reinforcement learning Mnih.Heess.Graves.ea.2014 Training . Given that the given framework dominates in the above figure , Therefore, the model under this framework will become the focus of our attention in this chapter .

summary ：

• Convolution 、 Full connection 、 The pool layer only considers non random clues
• Attention mechanism shows consideration of random clues
  • Each clue is called a query （query）
  • Each input is a value （value） And random clues （key） Right
  • Select certain inputs in a biased way through the attention pooling layer

2.3 Visualization of attention

   The average pooling layer can be regarded as the weighted average of the input , Its weight is evenly distributed . actually , The result of attention pooling is the total value of weighted average , The weight is calculated between a given query and different keys .

import torch
from d2l import torch as d2l

#  Visual weights ： Input is matrices
#  shape （ Number of lines to display 、 Number of columns to display 、 Number of queries 、 Number of keys ）
def show_heatmaps(matrices,xlabel,ylabel,titles=None,figsize=(2.5,2.5),cmap='Reds'):
    d2l.use_svg_display()
    num_rows,num_cols = matrices.shape[0],matrices.shape[1]
    fig,axes = d2l.plt.subplots(num_rows,num_cols,figsize=figsize,sharex=True,sharey=True,squeeze=False)
    for i ,(row_axes,row_matrices) in enumerate(zip(axes,matrices)):
        for j,(ax,matrix) in enumerate(zip(row_axes,row_matrices)):
            pcm = ax.imshow(matrix.detach().numpy(),cmap=cmap)
            if i ==num_rows -1:
                ax.set_xlabel(xlabel)
            if j == 0:
                ax.set_ylabel(ylabel)
            if titles:
                ax.set_title(title(titles[j]))
    fig.colorbar(pcm,ax=axes,shrink=0.6)

#  Use a simple example to demonstrate , When the query and key are the same, the attention weight is 1,
attention_weights = torch.eye(10).reshape((1, 1, 10, 10))
show_heatmaps(attention_weights, xlabel='Keys', ylabel='Queries')

3、 ... and 、 Attention pooling ：Nadaraya-Watson Nuclear regression

   In the know Query-key-value The main components of attention mechanism under the framework . Take a look back. , Inquire about （ Autonomous prompt ） Sum key （ Involuntary prompt ） The interaction between them forms Attention pooling （attention pooling）. Attention pooling selectively aggregates values （ Sensory input ） To generate the final output 1964 Put forward in Nadaraya-Watson The kernel regression model is a simple and complete example , It can be used to demonstrate machine learning with attention mechanism .

import torch
from torch import nn
from d2l import torch as d2l

3.1 Generate data set

   Simplicity , Consider the following regression problem ： For a given pair “ Input － Output ” Data sets $\{(x_1,y_1),\dots ,(x_n,y_n)\}$, How to learn $f$ To predict any new input $x$ Output $\hat{y}=f(x)$？

   Generate an artificial data set according to the following nonlinear function , The noise term added is $ϵ$：

$$y_i=2\sin (x_i)+x_i^{0.8}+ϵ,$$

   among $ϵ$ To obey the mean is $0$ And the standard deviation is $0.5$ Is a normal distribution . At the same time $50$ Training samples and $50$ Three test samples . To better visualize attention patterns , The training samples entered will be sorted .

n_train = 50 # the number of train example
x_train,_ = torch.sort(torch.rand(n_train)*5) # the inputs of train example

def f(x):
    return 2*torch.sin(x)+x**0.8

y_train = f(x_train)+torch.normal(0.0,0.5,(n_train,))
x_test = torch.arange(0,5,0.1) 
y_truth = f(x_test) #the real outputs of train exaple
n_test = len(x_test)
n_test

50

3.2 The average pooling

   First use may be in this world “ The stupidest ” To solve the regression problem ： Calculate the average of the output values of all training samples based on the average pooling ：

$$f(x)=\frac{1}{n}\sum _{i=1}^n{y}_i,$$

As shown in the figure below , This estimator is really not smart enough .

#  Draw all training samples （ circular ）, Generate a function with no real noise f（ Marked as “truth”）; The prediction function learned （“Pred”）
def plot_kernel_reg(y_hat):
    d2l.plot(x_test, [y_truth, y_hat], 'x', 'y', legend=['Truth', 'Pred'],
             xlim=[0, 5], ylim=[-1, 5])
    d2l.plt.plot(x_train, y_train, 'o', alpha=0.5);

y_hat = torch.repeat_interleave(y_train.mean(), n_test)
plot_kernel_reg(y_hat)

3.3 Nonparametric attention pooling

   obviously , Average pooling ignores input $x_i$. therefore Nadaraya Nadaraya.1964 and WastonWatson.1964 Came up with a better idea , The output is adjusted according to the position of the input $y_i$ Weighted ：

$$f(x)=\sum _{i=1}^n\frac{K(x-x_i)}{{\sum }_{j=1}^{n}K(x-x_j)}{y}_i,$$
among $K$ yes Kernel function *（kernel）. The estimator described by the formula is called Nadaraya-Watson Nuclear regression （Nadaraya-Watson kernel regression）( Isn't this guy a weighted average ！！, Measure content closer to new additions ). We won't go into the details of kernel function here . Recall the attention mechanism framework , We can rewrite the equation from the perspective of attention mechanism to become a more general Attention pooling （attention pooling） The formula ：

$$f(x)=\sum _{i=1}^n\alpha (x,x_i)y_i,$$

   among $x$ It's a query ,$(x_i,y_i)$ yes “ key － value ” Yes . Comparing the two formulas, we can find that attention pooling is $y_i$ The weighted average of . Will query $x$ Sum key $x_i$ The relationship between is modeled as Attention weight （attetnion weight） $\alpha (x,x_i)$, This weight will be assigned to each corresponding value $y_i$. For any query , Models in all “ key － value ” The attention weight of each pair is an effective probability distribution ： They are nonnegative numbers , And the sum is one .

In order to better understand attention pooling , Just consider one Gaussian kernel （Gaussian kernel）, The definition for （u Time distance $x-x_j$）：

$$K(u)=\frac{1}{\sqrt{2\pi }}\exp (-\frac{u^2}{2}).$$

Substituting Gaussian kernel into the above two formulas will get

$$\begin{array}{rl}f(x)& =\sum _{i=1}^n\alpha (x,x_i)y_i\\ & =\sum _{i=1}^n\frac{\exp \left(-\frac{1}{2}(x-x_i{)}^2\right)}{{\sum }_{j=1}^n\exp \left(-\frac{1}{2}(x-x_j{)}^2\right)}{y}_i\\ & =\sum _{i=1}^n\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}\mathrm{m}\mathrm{a}\mathrm{x}\left(-\frac{1}{2}(x-x_i{)}^2\right)y_i.\end{array}$$

   If a key $x_i$ The closer to a given query $x$, Then assign the corresponding value to this key $y_i$ Of The greater the attention weight , That is to say Get more attention . It is worth noting that ,Nadaraya-Watson Kernel regression is a nonparametric model ; therefore , The attention pooling derived from it is Nonparametric attention pooling （nonparametric attention pooling）. Next , We will draw the prediction results based on this nonparametric attention pooling model . The result is that the prediction line is smooth , And the line produced by average pooling is closer to reality .

# `X_repeat`  The shape of the : (`n_test`, `n_train`),
#  Each line contains the same test input （ for example ： Same query ）
X_repeat = x_test.repeat_interleave(n_train).reshape((-1,n_train))
# `x_train`  Contains keys .`attention_weights`  The shape of the ：(`n_test`, `n_train`),
#  Each row contains the value of each query to be given （`y_train`） The weight of attention allocated between 
attention_weights = nn.functional.softmax(-(X_repeat-x_train)**2/2,dim=1)
y_hat = torch.matmul(attention_weights,y_train)
plot_kernel_reg(y_hat)

show_heatmaps(
    attention_weights.unsqueeze(0).unsqueeze(0),
    xlabel='Sorted training inputs', ylabel='Sorted testing inputs')

3.4 Attention pooling with parameters

   Nonparametric Nadaraya-Watson Nuclear regression has Uniformity （consistency） The advantages of ： If there's enough data , The model will converge to the optimal result . For all that , We can still easily integrate learnable parameters into attention pooling . for example , It is slightly different from nonparametric attention pooling , In the following query $x$ Sum key $x_i$ The distance between is multiplied by the learnable parameter $w$：

$$\begin{array}{rl}f(x)& =\sum _{i=1}^n\alpha (x,x_i)y_i\\ & =\sum _{i=1}^n\frac{\exp \left(-\frac{1}{2}((x-x_i)w{)}^2\right)}{{\sum }_{j=1}^n\exp \left(-\frac{1}{2}((x-x_i)w{)}^2\right)}{y}_i\\ & =\sum _{i=1}^n\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}\mathrm{m}\mathrm{a}\mathrm{x}\left(-\frac{1}{2}((x-x_i)w{)}^2\right)y_i.\end{array}$$

   below , We will learn the parameters of attention pooling by training this model .

3.4.1 Batch matrix multiplication

   In order to calculate the attention of small batch data more effectively , We can use the batch matrix multiplication provided in the deep learning development framework . Suppose the first small batch of data contains $n$ Matrix ${\mathbf{X}}_1,\dots ,{\mathbf{X}}_n$, Shape is $a\times b$, The second small batch contains $n$ Matrix ${\mathbf{Y}}_1,\dots ,{\mathbf{Y}}_n$, Shape is $b\times c$. Their batch matrix multiplication results in $n$ Matrix ${\mathbf{X}}_1{\mathbf{Y}}_1,\dots ,{\mathbf{X}}_n{\mathbf{Y}}_n$, Shape is $a\times c$. therefore , Suppose that the shapes of the two tensors are $(n,a,b)$ and $(n,b,c)$ , The shape of their batch matrix multiplication output is $(n,a,c)$.

X = torch.ones((2,1,4))
Y = torch.ones((2,4,6))
torch.bmm(X,Y).shape

torch.Size([2, 1, 6])

#  In the attention mechanism , We can use small batch matrix multiplication to calculate the weighted average of the median of small batch data 
weights = torch.ones((2,10))*0.1
value = torch.arange(20.0).reshape((2,10))
torch.bmm(weights.unsqueeze(1),value.unsqueeze(-1))

tensor([[[ 4.5000]],
        [[14.5000]]])

3.4.2 Model definition

w Control the smoothness of Gaussian kernel

class NWKernelRegression(nn.Module):
    def __init__(self,**kwargs):
        super().__init__(**kwargs)
        self.w = nn.Parameter(torch.rand((1,),requires_grad=True))
    def forward(self,queries,keys,values):
        # `queries`  and  `attention_weights`  The shape of the :( Number of queries , “ key － value ” Number of pairs )
        queries = queries.repeat_interleave(keys.shape[1]).reshape((-1,keys.shape[1]))
        self.attention_weights = nn.functional.softmax(-((queries-keys)*self.w)**2/2,dim=1)
        # `values`  The shape of the :( Number of queries , “ key － value ” Number of pairs )
        return torch.bmm(self.attention_weights.unsqueeze(1),values.unsqueeze(-1)).reshape(-1)

3.4.2 model training

# `X_tile`  The shape of the : (`n_train`, `n_train`),  Each line contains the same training input 
X_tile = x_train.repeat((n_train, 1))
# `Y_tile`  The shape of the : (`n_train`, `n_train`),  Each line contains the same training output 
Y_tile = y_train.repeat((n_train, 1))
# `keys`  The shape of the : ('n_train', 'n_train' - 1)
keys = X_tile[(1 - torch.eye(n_train)).type(torch.bool)].reshape(
    (n_train, -1))
# `values`  The shape of the : ('n_train', 'n_train' - 1)
values = Y_tile[(1 - torch.eye(n_train)).type(torch.bool)].reshape(
    (n_train, -1))

net = NWKernelRegression()
loss = nn.MSELoss(reduction='none')
trainer = torch.optim.SGD(net.parameters(), lr=0.5)
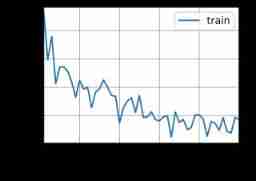
animator = d2l.Animator(xlabel='epoch', ylabel='loss', xlim=[1, 5])

for epoch in range(5):
    trainer.zero_grad()
    #  Be careful ：L2 Loss = 1/2 * MSE Loss.
    # PyTorch  Of  MSE Loss  And  MXNet  Of  L2Loss  one less  2  Factor of , So it is halved .
    l = loss(net(x_train, keys, values), y_train) / 2
    l.sum().backward()
    trainer.step()
    print(f'epoch {
      epoch + 1}, loss {
      float(l.sum()):.6f}')
    animator.add(epoch + 1, float(l.sum()))

# `keys`  The shape of the : (`n_test`, `n_train`),  Each line contains the same training input （ for example ： The same key ）
keys = x_train.repeat((n_test, 1))
# `value`  The shape of the : (`n_test`, `n_train`)
values = y_train.repeat((n_test, 1))
y_hat = net(x_test, keys, values).unsqueeze(1).detach()
plot_kernel_reg(y_hat)

show_heatmaps(
    net.attention_weights.unsqueeze(0).unsqueeze(0),
    xlabel='Sorted training inputs', ylabel='Sorted testing inputs')

Four 、 summary

• Human attention is limited 、 Precious and scarce resources .
• Subjects used involuntary and autonomous cues to selectively guide attention . The former is based on prominence , The latter depends on the task .
• The difference between the attention mechanism and the full connection layer or pooling layer stems from the increased autonomous prompts .
• Because it contains autonomous prompts , Note that the mechanism is different from the fully connected layer or pool layer .
• Attention mechanism biases selection towards value through attention pooling （ Sensory input ）, It contains queries （ Autonomous prompt ） Sum key （ Involuntary prompt ）. Keys and values are paired .
• We can visualize the attention weight between queries and keys .
• Nadaraya-Watson Kernel regression is an example of machine learning with attention mechanism .
• Nadaraya-Watson The attention pooling of kernel regression is the weighted average of the output of training data . From the perspective of attention , The attention weight assigned to each value depends on the function that takes the key corresponding to the value and the query as input .
• Attention pooling can be divided into non parametric and parametric .