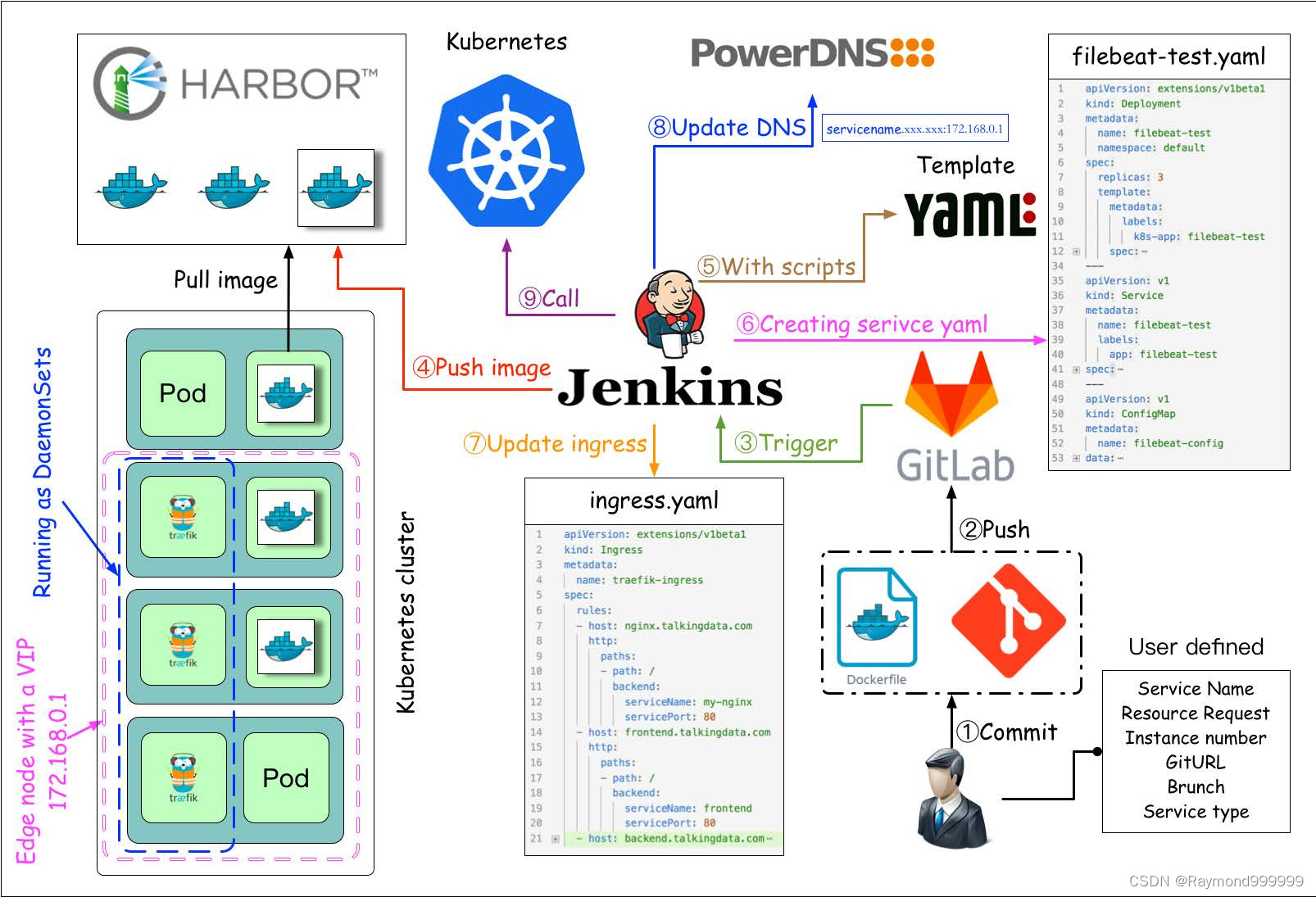
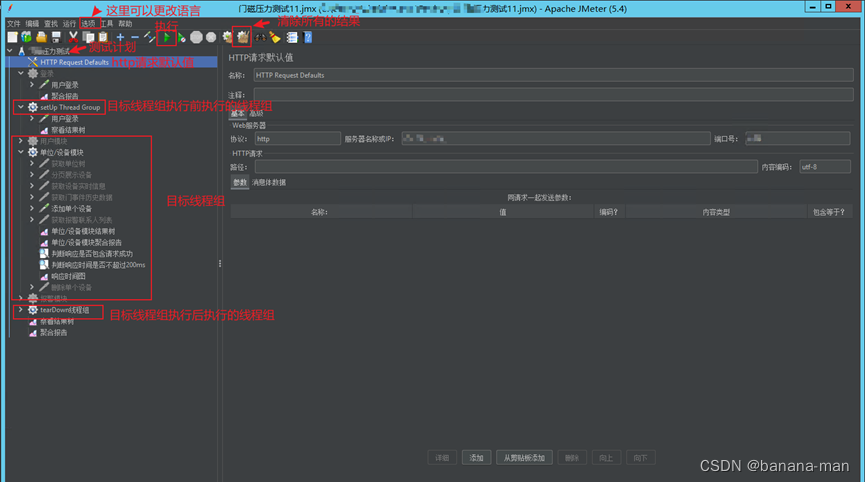
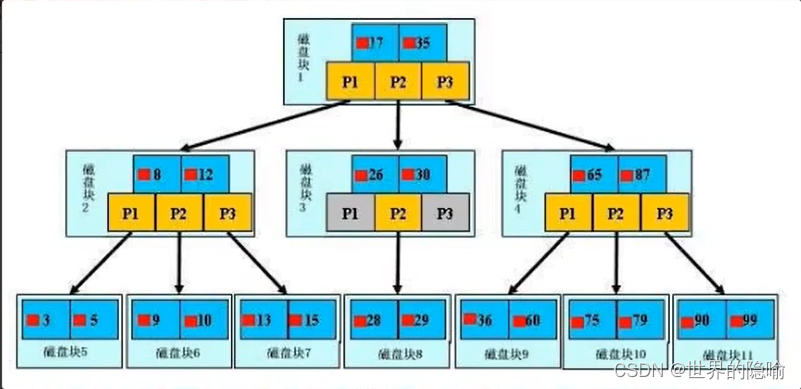
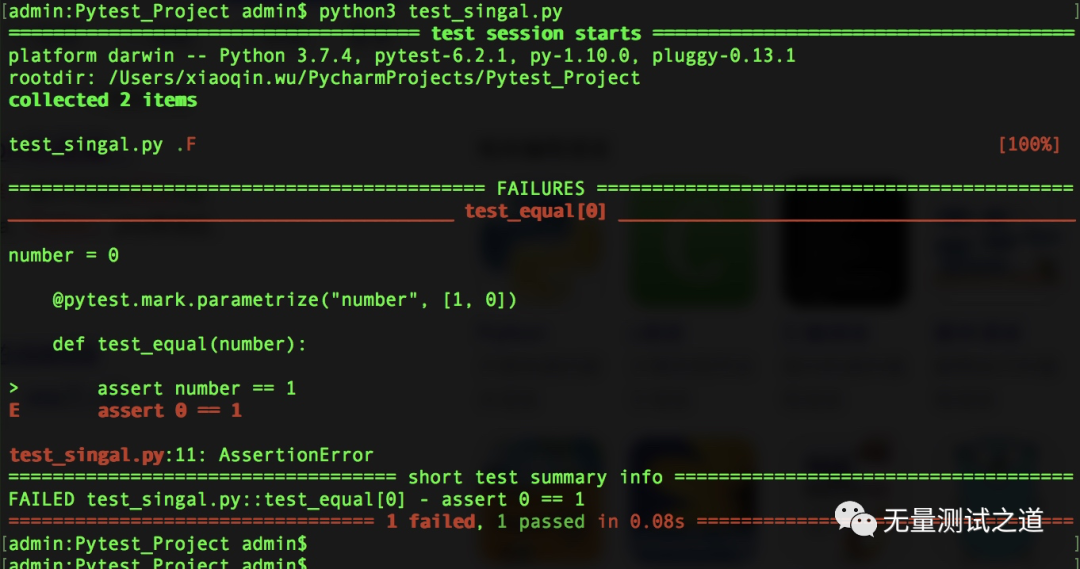
当前位置:网站首页>1.AVL树:左右旋-bite
1.AVL树:左右旋-bite
2022-07-06 23:30:00 【风生u】
AVL树的定义
左右子树的高度差的绝对值均不超过1的二叉搜索树.
有n个结点,时间复杂度是log以n为底2的对数;
AVL树的插入
左单旋:左旋就是旋转节点的右子树的左子树变为其新的右子树,同时旋转节点变成以前右子树的左子树
右端单旋:右旋就是旋转节点的左子树的右子树变成其新的左子树,同时旋转节点变成以前左子树的右子树
何时使用左旋,右旋,左右双旋,右左双选?
增加节点在要旋转节点的右子树的右子树上时:左旋,在要旋转节点的右子树的左子树上时:右左双旋.
增加节点在要旋转节点的左子树的左子树上时:右旋,在要旋转节点的左子树的右子树上时:左右双旋.
创建一个结点类:
public class TreeNode {
public int val;
public int bf;
public TreeNode left;
public TreeNode right;
public TreeNode parent;
public TreeNode(int val){
this.val = val;
}
}
插入元素:
public TreeNode root;//根节点
public boolean insert(int val) {
TreeNode node = new TreeNode(val);
if(root == null) {
root = node;
return true;
}
TreeNode parent = null;
TreeNode cur = root;
让node节点的双亲节点(parent)
while (cur != null) {
if(cur.val < val) {
parent = cur;
cur = cur.right;
}else if(cur.val == val) {
return false;
}else {
parent = cur;
cur = cur.left;
}
}
//cur == null
判断node,该插入parent的哪个子树.
if(parent.val < val) {
parent.right = node;
}else {
parent.left = node;
}
//
node.parent = parent;
cur = node;
// 平衡因子的修改
while (parent != null) {
//先看cur是parent的左还是右 决定平衡因子是++还是--
if(cur == parent.right) {
//如果是右树,那么右树高度增加 平衡因子++
parent.bf++;
}else {
//如果是左树,那么左树高度增加 平衡因子--
parent.bf--;
}
//检查当前的平衡因子 是不是绝对值 1 0 -1
if(parent.bf == 0) {
//说明已经平衡了
break;
}else if(parent.bf == 1 || parent.bf == -1) {
//继续向上去修改平衡因子
cur = parent;
parent = cur.parent;
}else {
if(parent.bf == 2) {
//右树高-》需要降低右树的高度
if(cur.bf == 1) {
//左旋
rotateLeft(parent);
}else {
//cur.bf == -1
//右左双旋
rotateRL(parent);
}
}else {
//parent.bf == -2 左树高-》需要降低左树的高度
if(cur.bf == -1) {
//右旋
rotateRight(parent);
}else {
//cur.bf == 1
//左右双旋
rotateLR(parent);
}
}
//上述代码走完就平衡了
break;
}
}
return true;
}
左单旋:左旋就是旋转节点的右子树的左子树变为其新的右子树,同时旋转节点变成以前右子树的左子树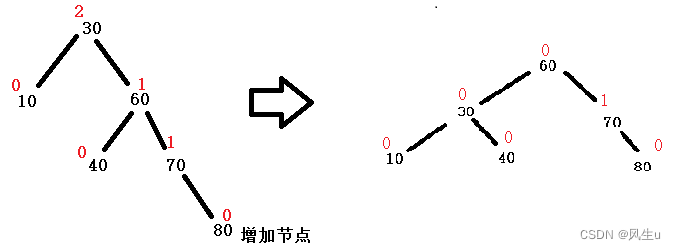
private void rotateLeft(TreeNode parent) {
//获取左旋节点的右子树
TreeNode subR = parent.right;
//获取左旋节点的右子树的左子树
TreeNode subRL = subR.left;
//左旋节点的右子树变为左旋节点旧右子树的左子树
parent.right = subRL;
//旧右子树的左子树变为左旋节点
subR.left = parent;
//如果当前旧右子树的左子树不为空,则让其双亲节点指向左旋节点.
if(subRL != null) {
subRL.parent = parent;
}
//先保存左旋点的双亲节点,好让其指向subR
TreeNode pParent = parent.parent;
parent.parent = subR;
判断左旋节点是否是根节点
if(root == parent) {
root = subR;
root.parent = null;
}else {
//判断左旋节点是双亲节点的哪个节点.
if(pParent.left == parent) {
pParent.left = subR;
}else {
pParent.right = subR;
}
subR.parent = pParent;
}
//调整平衡因子
subR.bf = parent.bf = 0;
}
右端单旋:右旋就是旋转节点的左子树的右子树变成其新的左子树,同时旋转节点变成以前左子树的右子树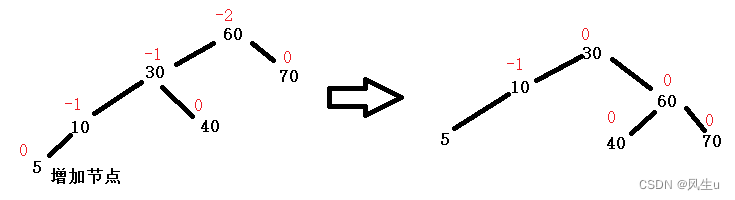
private void rotateRight(TreeNode parent) {
TreeNode subL = parent.left;
TreeNode subLR = subL.right;
parent.left = subLR;
subL.right = parent;
//没有subLR
if(subLR != null) {
subLR.parent = parent;
}
//必须先记录
TreeNode pParent = parent.parent;
parent.parent = subL;
//检查 当前是不是就是根节点
if(parent == root) {
root = subL;
root.parent = null;
}else {
//不是根节点,判断这棵子树是左子树还是右子树
if(pParent.left == parent) {
pParent.left = subL;
}else {
pParent.right = subL;
}
subL.parent = pParent;
}
subL.bf = 0;
parent.bf = 0;
}
左右双旋:增加节点在要旋转节点的左子树的左子树上时:右旋,在要旋转节点的左子树的右子树上时:左右双旋.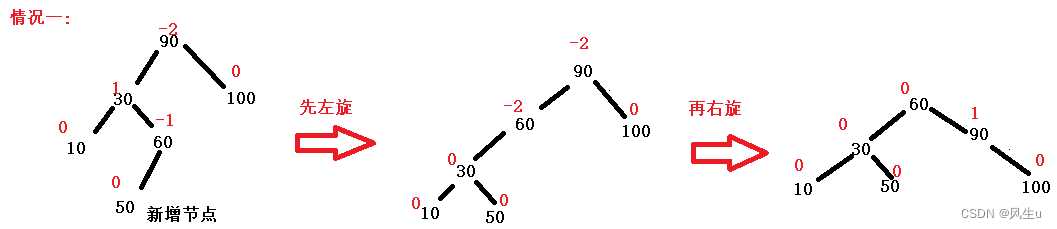
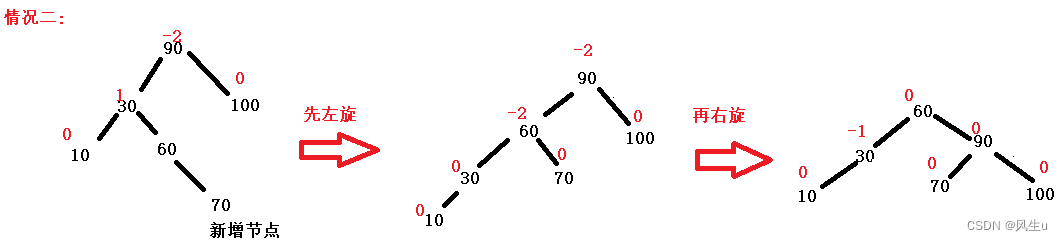
private void rotateLR(TreeNode parent) {
TreeNode subL = parent.left;
TreeNode subLR = subL.right;
int bf = subLR.bf;
rotateLeft(parent.left);
rotateRight(parent);
//由dubLT.bf的值(-1/1)调整平衡因子.
if(bf == -1) {
subL.bf = 0;
subLR.bf = 0;
parent.bf = 1;
}else if(bf == 1){
subL.bf = -1;
subLR.bf = 0;
parent.bf = 0;
}
}
右左双旋:增加节点在要旋转节点的右子树的右子树上时:左旋,在要旋转节点的右子树的左子树上时:右左双旋.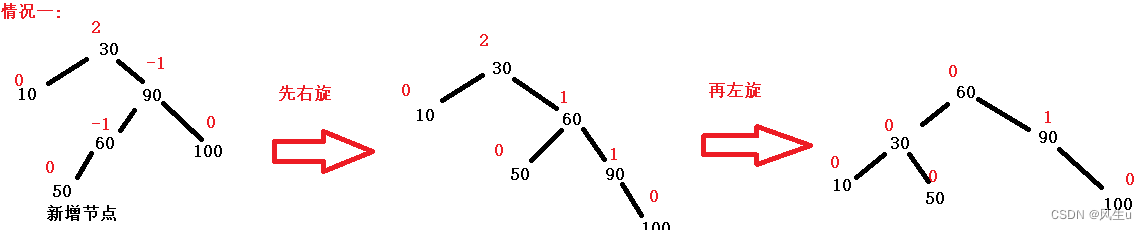
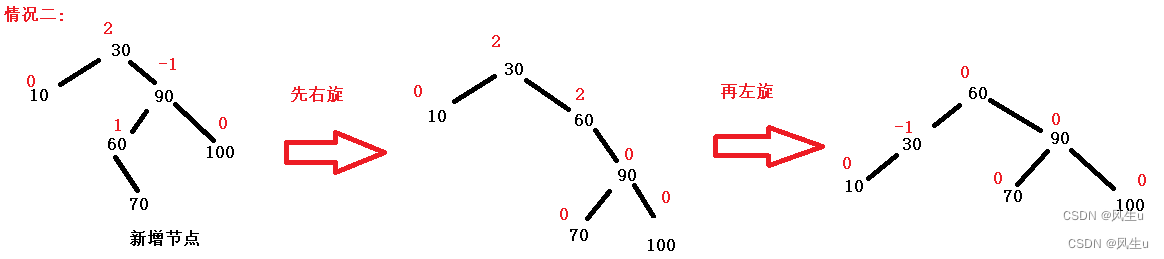
//右左双旋
private void rotateRL(TreeNode parent) {
TreeNode subR = parent.right;
TreeNode subRL = subR.left;
int bf = subRL.bf;
rotateR(parent.right);
rotateL(parent);
if(bf == -1){
parent.bf = 0;
subR.bf = 0;
subRL.bf = 1;
}else if(bf == 1){
parent.bf = -1;
subR.bf = 0;
subRL.bf = 0;
}
}
判断是否是AVL树
private int height(TreeNode root) {
if(root == null) return 0;
int leftH = height(root.left);
int rightH = height(root.right);
return leftH > rightH ? leftH+1 : rightH+1;
}
public boolean isBalanced(TreeNode root) {
if(root == null) return true;
int leftH = height(root.left);
int rightH = height(root.right);
if(rightH-leftH != root.bf) {
System.out.println("这个节点:"+root.val+" 平衡因子异常");
return false;
}
return Math.abs(leftH-rightH) <= 1
&& isBalanced(root.left)
&& isBalanced(root.right);
}
AVL树的删除(待定)
边栏推荐
- Addressable pre Download
- 创始人负债10亿,开课吧即将“下课”?
- JHOK-ZBG2漏电继电器
- As we media, what websites are there to download video clips for free?
- Timer create timer
- 漏电继电器JELR-250FG
- QT simple layout box model with spring
- Longest common subsequence (LCS) (dynamic programming, recursive)
- No experts! Growth secrets for junior and intermediate programmers and "quasi programmers" who are still practicing in Universities
- Development thoughts of adding new requirements in secondary development
猜你喜欢
随机推荐
Two person game based on bevy game engine and FPGA
说一说MVCC多版本并发控制器?
PMP证书有没有必要续期?
CentOS 7.9 installing Oracle 21C Adventures
Leetcode(417)——太平洋大西洋水流问题
AOSP ~binder communication principle (I) - Overview
Let f (x) = Σ x^n/n^2, prove that f (x) + F (1-x) + lnxln (1-x) = Σ 1/n^2
U++ game learning notes
QT控件样式系列(一)之QSlider
batch size设置技巧
[opencv] image morphological operation opencv marks the positions of different connected domains
《2》 Label
c语言神经网络基本代码大全及其含义
ScheduledExecutorService定时器
TabLayout修改自定义的Tab标题不生效问题
Full link voltage test: the dispute between shadow database and shadow table
磁盘监控相关命令
一个酷酷的“幽灵”控制台工具
Redis如何实现多可用区?
Array initialization of local variables