Leetcode（417）——太平洋大西洋水流问题

题目

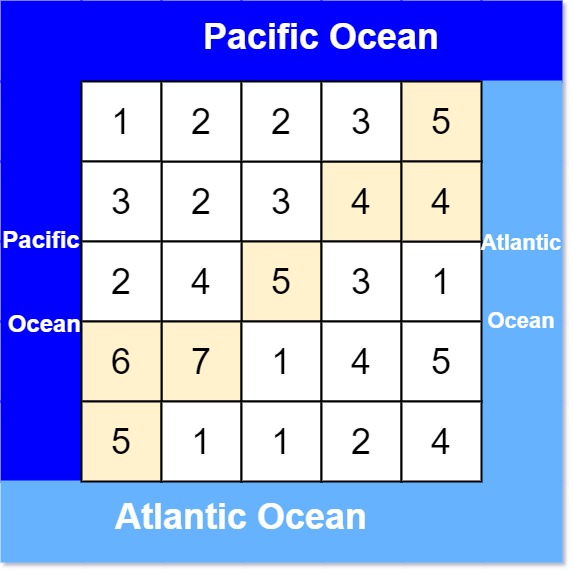
有一个 $m\times n$ 的矩形岛屿，与 太平洋 和 大西洋 相邻。 “太平洋” 处于大陆的左边界和上边界，而 “大西洋” 处于大陆的右边界和下边界。

这个岛被分割成一个由若干方形单元格组成的网格。给定一个 $m\times n$ 的整数矩阵 heights ， heights[r][c] 表示坐标 (r, c) 上单元格 高于海平面的高度 。

岛上雨水较多，如果相邻单元格的高度 小于或等于 当前单元格的高度，雨水可以直接向北、南、东、西流向相邻单元格。水可以从海洋附近的任何单元格流入海洋。

返回网格坐标 result 的 2D 列表 ，其中 result[i] = [ri, ci] 表示雨水从单元格 (ri, ci) 流动 既可流向太平洋也可流向大西洋 。

示例 1：

输入: heights = [[1,2,2,3,5],[3,2,3,4,4],[2,4,5,3,1],[6,7,1,4,5],[5,1,1,2,4]]
输出: [[0,4],[1,3],[1,4],[2,2],[3,0],[3,1],[4,0]]

示例 2：

输入: heights = [[2,1],[1,2]]
输出: [[0,0],[0,1],[1,0],[1,1]]

提示：

• m == heights.length
• n == heights[r].length
• $1$ <= m, n <= $200$
• $0$ <= heights[r][c] <= $10^5$

题解

从边界开始反向搜索，以减少时间复杂度

方法一：DFS

思路

​​  雨水的流动方向是从高到低，每个单元格上的雨水只能流到高度小于等于当前单元格的相邻单元格。从一个单元格开始，通过搜索的方法模拟雨水的流动，则可以判断雨水是否可以从该单元格流向海洋。

​​  如果直接以每个单元格作为起点模拟雨水的流动，则会重复遍历每个单元格，导致时间复杂度过高。为了降低时间复杂度，可以从矩阵的边界开始反向搜索寻找雨水流向边界的单元格，反向搜索时，每次只能移动到高度相同或更大的单元格。

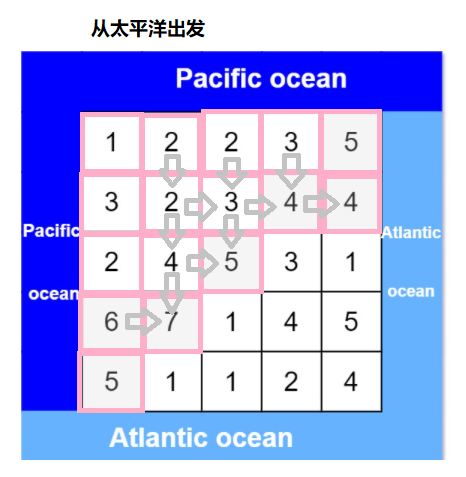
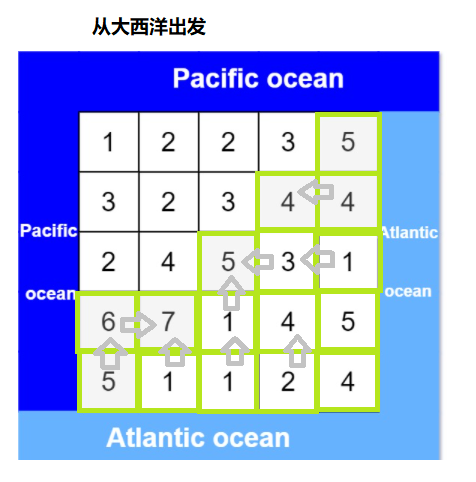
​​  由于矩阵的左边界和上边界是太平洋，矩阵的右边界和下边界是大西洋，因此从矩阵的左边界和上边界开始反向搜索即可找到雨水流向太平洋的单元格，从矩阵的右边界和下边界开始反向搜索即可找到雨水流向大西洋的单元格。

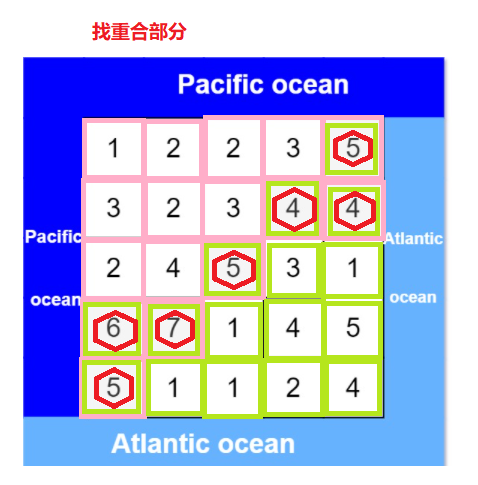
​​  可以使用深度优先搜索实现反向搜索，搜索过程中需要记录每个单元格是否可以从太平洋反向到达以及是否可以从大西洋反向到达。反向搜索结束之后，遍历每个网格，如果一个网格既可以从太平洋反向到达也可以从大西洋反向到达，则该网格满足太平洋和大西洋都可以到达，将该网格添加到答案中。

代码实现

Leetcode 官方题解：

static const int dirs[4][2] = {
    {
    -1, 0}, {
    1, 0}, {
    0, -1}, {
    0, 1}};

class Solution {
    
public:
    vector<vector<int>> heights;

    void dfs(int row, int col, vector<vector<bool>> & ocean) {
    
        int m = ocean.size();
        int n = ocean[0].size();
        if (ocean[row][col]) {
    
            return;
        }
        ocean[row][col] = true;
        for (int i = 0; i < 4; i++) {
    
            int newRow = row + dirs[i][0], newCol = col + dirs[i][1];
            if (newRow >= 0 && newRow < m && newCol >= 0 && newCol < n && heights[newRow][newCol] >= heights[row][col]) {
    
                dfs(newRow, newCol, ocean);
            }
        }
    }

    vector<vector<int>> pacificAtlantic(vector<vector<int>>& heights) {
    
        this->heights = heights;
        int m = heights.size();
        int n = heights[0].size();
        vector<vector<bool>> pacific(m, vector<bool>(n, false));
        vector<vector<bool>> atlantic(m, vector<bool>(n, false));

        for (int i = 0; i < m; i++) {
    
            dfs(i, 0, pacific);
        }
        for (int j = 1; j < n; j++) {
    
            dfs(0, j, pacific);
        }
        for (int i = 0; i < m; i++) {
    
            dfs(i, n - 1, atlantic);
        }
        for (int j = 0; j < n - 1; j++) {
    
            dfs(m - 1, j, atlantic);
        }
        vector<vector<int>> result;
        for (int i = 0; i < m; i++) {
    
            for (int j = 0; j < n; j++) {
    
                if (pacific[i][j] && atlantic[i][j]) {
    
                    vector<int> cell;
                    cell.emplace_back(i);
                    cell.emplace_back(j);
                    result.emplace_back(cell);
                }
            }
        }
        return result;
    }
};

我自己的：（递归）

class Solution {
    
    vector<int> direction{
    -1, 0, 1, 0, -1}; //用于遍历四个方位
    void DFS(vector<vector<int>>& heights, vector<vector<bool>>& ocean, int a, int b){
    
        ocean[a][b] = true;
        int p1, p2;
        for(int n = 0; n < 4; n++){
    
            p1 = a + direction[n];
            p2 = b + direction[n+1];
            if(0 > p1 || p1 >= heights.size() || 0 > p2 || p2 >= heights[0].size()) 
                continue;
            if(heights[p1][p2] >= heights[a][b] && ocean[p1][p2] == false) 
                DFS(heights, ocean, p1, p2);
        }
    }
public:
    vector<vector<int>> pacificAtlantic(vector<vector<int>>& heights) {
    
        // 从外到内
        int n = heights.size(), m = heights[0].size();
        vector<vector<int>> ans;
        vector<vector<bool>> Pacific_Ocean(n, vector<bool>(m, false));
        vector<vector<bool>> Atlantic_Ocean(n, vector<bool>(m, false));
        // 上下
        for(int i = 0; i < m; i++){
    
            DFS(heights, Pacific_Ocean, 0, i);
            DFS(heights, Atlantic_Ocean, n -1, i);
        }
        // 左右
        for(int i = 0; i < n; i++){
    
            DFS(heights, Pacific_Ocean, i, 0);
            DFS(heights, Atlantic_Ocean, i, m - 1);
        }
        for(int a = 0; a < n; a++){
    
            for(int b = 0; b < m; b++){
    
                if(Pacific_Ocean[a][b] && Atlantic_Ocean[a][b]) 
                    ans.push_back(vector<int>{
    a, b});
            }
        }
        return ans;
    }
};

复杂度分析

• 时间复杂度：$O(mn)$，其中 $m$ 和 $n$ 分别是矩阵 $\text{heights}$ 的行数和列数。深度优先搜索最多遍历每个单元格两次，寻找太平洋和大西洋都可以到达的单元格需要遍历整个矩阵，因此时间复杂度是 $O(mn)$。
• 空间复杂度：$O(mn)$，其中 $m$ 和 $n$ 分别是矩阵 $\text{heights}$ 的行数和列数。深度优先搜索的递归调用层数是 $O(mn)$，记录每个单元格是否可以到达太平洋和大西洋需要 $O(2\times mn)$ 的空间，因此空间复杂度是 $O(mn)$。

方法二：BFS

思路

​​  反向搜索也可以使用广度优先搜索实现。搜索过程中同样需要记录每个单元格是否可以从太平洋反向到达以及是否可以从大西洋反向到达。反向搜索结束之后，遍历每个网格，如果一个网格既可以从太平洋反向到达也可以从大西洋反向到达，则该网格满足太平洋和大西洋都可以到达，将该网格添加到答案中。

代码实现

Leetcode 官方题解：

static const int dirs[4][2] = {
    {
    -1, 0}, {
    1, 0}, {
    0, -1}, {
    0, 1}};

class Solution {
    
public:
    vector<vector<int>> heights;

    void bfs(int row, int col, vector<vector<bool>> & ocean) {
    
        if (ocean[row][col]) {
    
            return;
        }
        int m = heights.size();
        int n = heights[0].size();
        ocean[row][col] = true;
        queue<pair<int, int>> qu;
        qu.emplace(row, col);
        while (!qu.empty()) {
    
            auto [row, col] = qu.front();
            qu.pop();
            for (int i = 0; i < 4; i++) {
    
                int newRow = row + dirs[i][0], newCol = col + dirs[i][1];
                if (newRow >= 0 && newRow < m && newCol >= 0 && newCol < n && heights[newRow][newCol] >= heights[row][col] && !ocean[newRow][newCol]) {
    
                    ocean[newRow][newCol] = true;
                    qu.emplace(newRow, newCol);
                }
            }
        }
    }

    vector<vector<int>> pacificAtlantic(vector<vector<int>>& heights) {
    
        this->heights = heights;
        int m = heights.size();
        int n = heights[0].size();
        vector<vector<bool>> pacific(m, vector<bool>(n, false));
        vector<vector<bool>> atlantic(m, vector<bool>(n, false));

        for (int i = 0; i < m; i++) {
    
            bfs(i, 0, pacific);
        }
        for (int j = 1; j < n; j++) {
    
            bfs(0, j, pacific);
        }
        for (int i = 0; i < m; i++) {
    
            bfs(i, n - 1, atlantic);
        }
        for (int j = 0; j < n - 1; j++) {
    
            bfs(m - 1, j, atlantic);
        }
        vector<vector<int>> result;
        for (int i = 0; i < m; i++) {
    
            for (int j = 0; j < n; j++) {
    
                if (pacific[i][j] && atlantic[i][j]) {
    
                    vector<int> cell;
                    cell.emplace_back(i);
                    cell.emplace_back(j);
                    result.emplace_back(cell);
                }
            }
        }
        return result;
    }
};

我自己的：

class Solution {
    
    vector<int> direction{
    -1, 0, 1, 0, -1}; //用于遍历四个方位
    void BFS(vector<vector<int>>& heights, vector<vector<bool>>& ocean, int a, int b){
    
        queue<pair<int, int>> qu;
        ocean[a][b] = true;
        qu.push(make_pair(a, b));
        int n, m, nextn, nextm;
        while(!qu.empty()){
    
            n = qu.front().first;
            m = qu.front().second;
            qu.pop();
            for(int i = 0; i < 4; i++){
    
                nextn = n + direction[i];
                nextm = m + direction[i+1];
                if(0 > nextn || nextn >= heights.size() || 0 > nextm || nextm >= heights[0].size())
                    continue;
                if(heights[nextn][nextm] >= heights[n][m] && ocean[nextn][nextm] == false){
    
                    ocean[nextn][nextm] = true;
                    qu.push(make_pair(nextn, nextm));
                }
            }
        }
    }
public:
    vector<vector<int>> pacificAtlantic(vector<vector<int>>& heights) {
    
        // 从外到内
        int n = heights.size(), m = heights[0].size();
        vector<vector<int>> ans;
        vector<vector<bool>> Pacific_Ocean(n, vector<bool>(m, false));
        vector<vector<bool>> Atlantic_Ocean(n, vector<bool>(m, false));
        // 上下
        for(int i = 0; i < m; i++){
    
            BFS(heights, Pacific_Ocean, 0, i);
            BFS(heights, Atlantic_Ocean, n - 1, i);
        }
        // 左右
        for(int i = 0; i < n; i++){
    
            BFS(heights, Pacific_Ocean, i, 0);
            BFS(heights, Atlantic_Ocean, i, m - 1);
        }
        for(int a = 0; a < n; a++){
    
            for(int b = 0; b < m; b++){
    
                if(Pacific_Ocean[a][b] && Atlantic_Ocean[a][b]) 
                    ans.push_back(vector<int>{
    a, b});
            }
        }
        return ans;
    }
};

复杂度分析

• 时间复杂度：$O(mn)$，其中 $m$ 和 $n$ 分别是矩阵 $\text{heights}$ 的行数和列数。广度优先搜索最多遍历每个单元格两次，寻找太平洋和大西洋都可以到达的单元格需要遍历整个矩阵，因此时间复杂度是 $O(mn)$。
• 空间复杂度：$O(mn)$，其中 $m$ 和 $n$ 分别是矩阵 $\text{heights}$ 的行数和列数。广度优先搜索的队列空间是 $O(mn)$，记录每个单元格是否可以到达太平洋和大西洋需要 $O(2\times mn)$ 的空间，因此空间复杂度是 $O(mn)$。

方法三：并查集

思路

​​  其中维护连通性部分可以使用「并查集」来做：起始将与太平洋相邻的边缘格子与 Pacific_Ocean 连通，将与大西洋相邻的边缘格子与 Atlantic_Ocean 连通，然后运行一遍方法一或方法二中的 DFS/BFS，最后将既和 Pacific_Ocean 连通又和 Atlantic_Ocean 连通的格子加入答案。

代码实现

我自己的：

无，忘记写了

复杂度分析

• 时间复杂度：$O(mn)$，其中 $m$ 和 $n$ 分别是矩阵 $\text{heights}$ 的行数和列数。DFS 和 BFS 最多遍历每个单元格两次，寻找太平洋和大西洋都可以到达的单元格需要遍历整个矩阵，因此时间复杂度是 $O(mn)$。
• 空间复杂度：$O(mn)$，其中 $m$ 和 $n$ 分别是矩阵 $\text{heights}$ 的行数和列数。BFS 的队列空间是 $O(mn)$，而 DFS 的递归栈空间或辅助栈空间是 $O(mn)$。记录每个单元格是否可以到达太平洋和大西洋需要 $O(2\times mn)$ 的空间，因此空间复杂度是 $O(mn)$。