当前位置:网站首页>221. Largest Square
221. Largest Square
2022-07-31 01:52:00 【ZNineSun】
打卡!!!每日一题
今天继续给大家分享一道动态规划类型的题目,However, the state transition equation of this topic is more difficult to understand,I will give you a detailed analysis
题目描述:
在一个由 ‘0’ 和 ‘1’ 组成的二维矩阵内,找到只包含 ‘1’ 的最大正方形,并返回其面积.
题目示例:

本题思路很简单,直接暴力解决,两个for循环遍历,Traverse all the way to the bottom right node,Then find an area maximum,Because the time complexity is too high,Also sorry for our IQ(PS:Just listen to my bragging,In the real written test or interview, you must use the fastest speed to solve it,只要能AC就是厉害),Next we discuss the solution of dynamic programming.
我们定义dp[i][j],表示以(i,j)为右下角的,且只包含 1 的正方形的边长最大值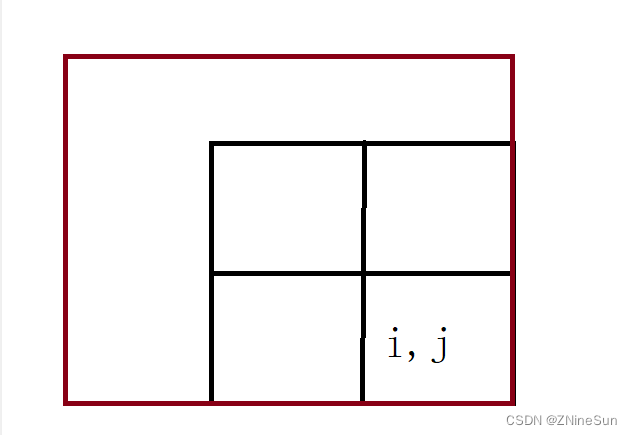
通俗来讲,Like the corresponding square under the red area shown above,Of course the square might not be that big,I just drew a random one for everyone to understand the meaning of the lower right corner.
如果我们能计算出所有 dp(i,j) 的值,那么其中的最大值即为矩阵中只包含 1 的正方形的边长最大值,其平方即为最大正方形的面积.
那么如何计算 dp 中的每个元素值呢?对于每个位置 (i, j),检查在矩阵中该位置的值:
- 如果该位置的值是 0,则 dp(i, j) = 0,因为当前位置不可能在由 1 组成的正方形中;
- 如果该位置的值是 1,则 dp(i,j) 的值由其上方、左方和左上方的三个相邻位置的 dp 值决定.具体而言,当前位置的元素值等于三个相邻位置的元素中的最小值加 1,状态转移方程如下:
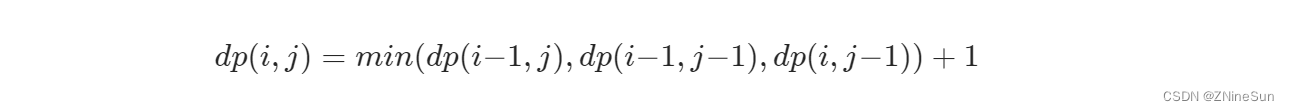
Let me help you understand why the minimum of these three is taken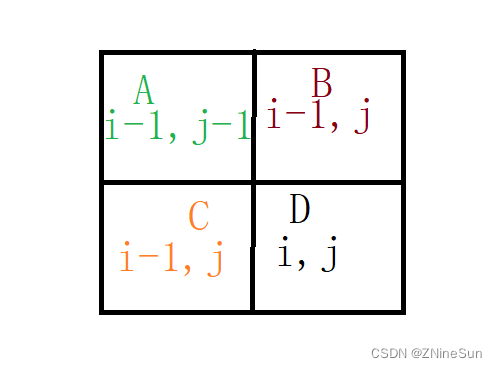
我们假设A,B,C的形状如下: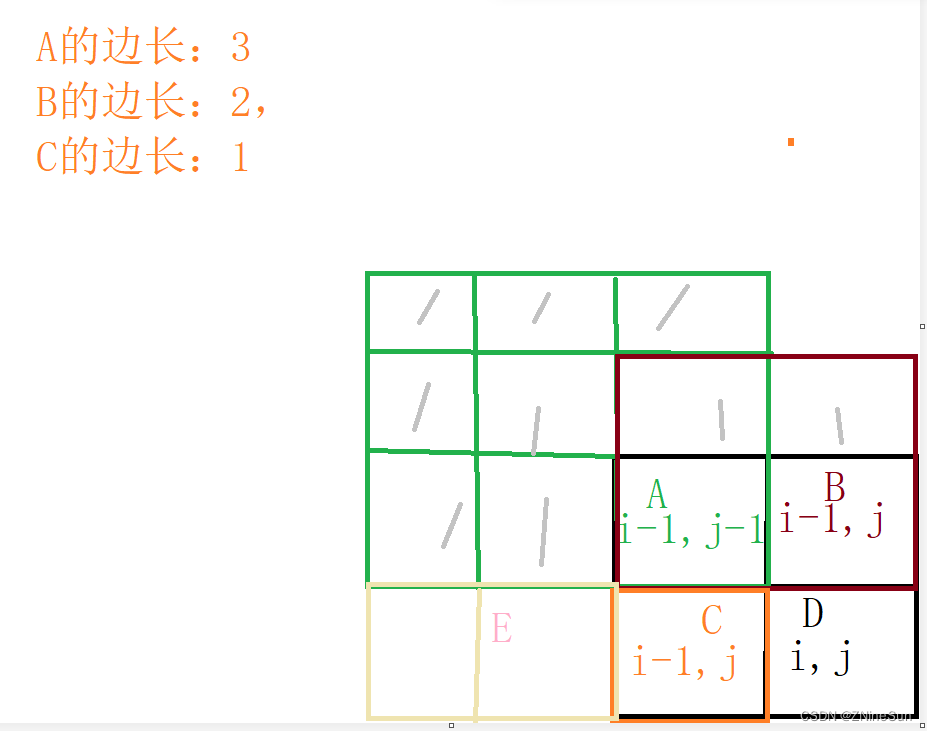
说明EThe value in the area must be 0,否则的话CThe side length can be taken2了
如果Dthe side length ofA的边长+1,即D的边长=4,Then it consists of a large square,一定包含E区域,这就不合理了,Because the title requires that our squares must all be1
如果还是不理解,下面留言吧,实在不行,I have time to record a video to explain it to you.
If this is understood,代码就很简单了:
public int maximalSquare(char[][] matrix) {
int row = matrix.length;
int coloumn = matrix[0].length;
if (row <= 1 && coloumn <= 1) {
return matrix[0][0];
}
int[][] dp = new int[row][coloumn];
for (int r = 0; r < row; r++) {
for (int c = 0; c < coloumn; c++) {
if (matrix[r][c] == '0') {
dp[r][c] = 0;
} else {
if (r - 1 < 0 || c - 1 < 0) {
dp[r][c] = 1;
} else {
dp[r][c] = Math.min(Math.min(dp[r][c - 1], dp[r - 1][c]), dp[r - 1][c - 1]) + 1;
}
}
}
}
int max = dp[0][0];
for (int i = 0; i < row; i++) {
for (int j = 0; j < coloumn; j++) {
max = Math.max(dp[i][j], max);
}
}
return max * max;
}
边栏推荐
猜你喜欢
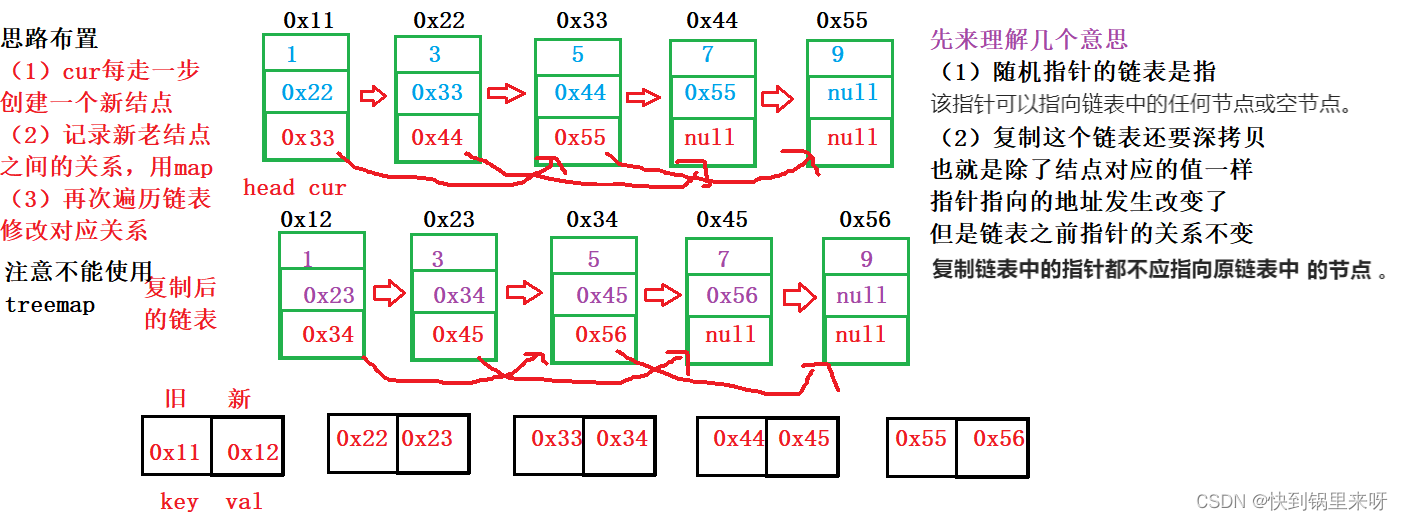
【Map与Set】之LeetCode&牛客练习

rpm install postgresql12

Fiddler抓包模拟弱网络环境测试
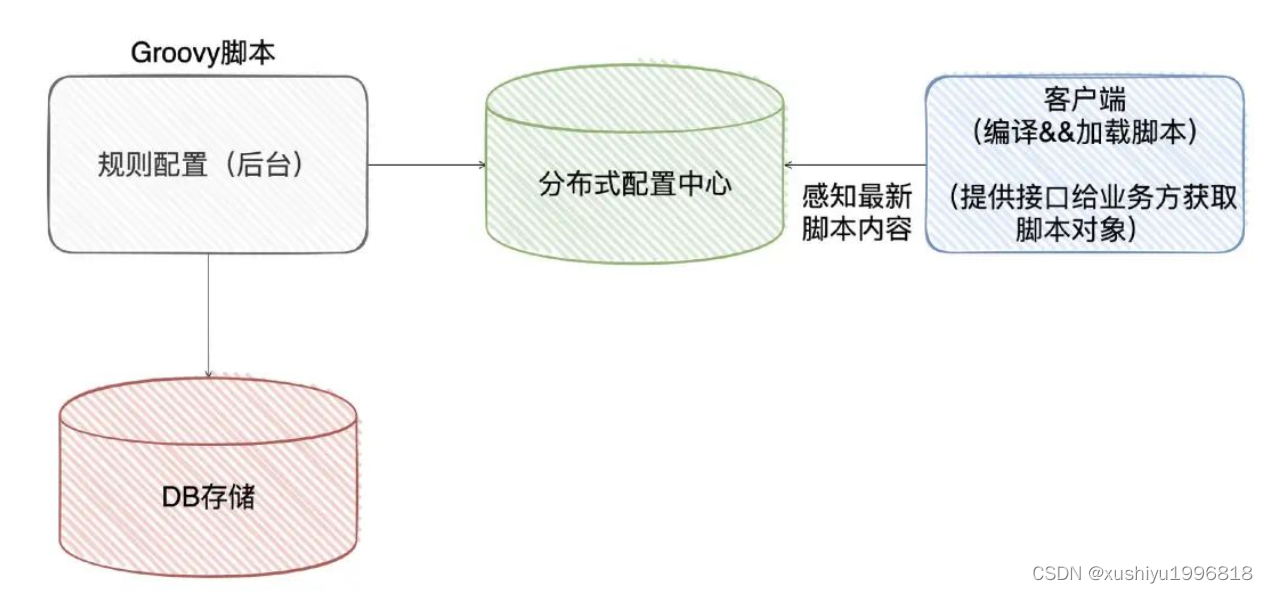
系统需求多变如何设计

ShardingJDBC基本介绍

Arbitrum 专访 | L2 Summer, 脱颖而出的 Arbitrum 为开发者带来了什么?

手把手教你配置Jenkins自动化邮件通知

Shell script to loop through values in log file to sum and calculate average, max and min

《云原生的本手、妙手和俗手》——2022全国新高考I卷作文
Maximum monthly salary of 20K?The average salary is nearly 10,000... What is the experience of working in a Huawei subsidiary?
随机推荐
《云原生的本手、妙手和俗手》——2022全国新高考I卷作文
Shell 脚本循环遍历日志文件中的值进行求和并计算平均值,最大值和最小值
一个无经验的大学毕业生,可以转行做软件测试吗?我的真实案例
蛮力法/邻接矩阵 广度优先 有向带权图 无向带权图
221. 最大正方形
力扣每日一题-第46天-704. 二分查找
android的webview缓存相关知识收集
leetcode-1161:最大层内元素和
Maximum monthly salary of 20K?The average salary is nearly 10,000... What is the experience of working in a Huawei subsidiary?
The effective square of the test (one question of the day 7/29)
蛮力法/邻接表 广度优先 有向带权图 无向带权图
关于Redis相关内容的基础学习
Drools Rule Properties, Advanced Syntax
ShardingJDBC使用总结
曼城推出可检测情绪的智能围巾,把球迷给整迷惑了
Force buckled brush the stairs (7/30)
系统需求多变如何设计
《MySQL数据库进阶实战》读后感(SQL 小虚竹)
MySQL的安装教程(嗷嗷详细,包教包会~)
keep-alive cache component